在这封信中,从幼时的见面与传闻,到战争年代的四处流浪,与生活、与命运抗争,含辛茹苦抚养子女,谢觉哉以姜一生命历程中的几个片段,向我们解释了这位平凡的劳动女性不平凡的一生,让人肃然起敬。信中所叙述的姜一的遭遇正是旧中国妇女命运的缩影,具有极高的社会史料价值。在这些背景之下,谢觉哉笔下姜一的形象也逐渐丰满、高大起来。......
2023-12-03
美国著名的几何学家佩多在一篇题为《数学经验》的文章里,谈到这样一件有趣的事情:
一个经济学家打电话问他一个问题。这位经济学家说,他研究的一种新的经济理论,涉及这样一个几何命题:正三角形内的任一点,到三角形3边距离之和为定值。他问佩多这个命题对不对?如果对,又是为什么?
这位经济学家还说,他曾请教过别的数学专家,结果都没有得到满意的回答。
当然,佩多教授马上回答了这个问题。如图5-1,△ABC是正三角形,AB=BC=CA=a,点P在△ABC内,P到BC、CA、AB三边的距离顺次是x、y、z。显然有△PBC+△PCA+△PAB=△ABC,也就是
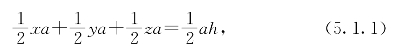
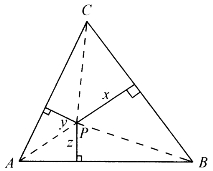
图5-1
这里h是△ABC的高。从(5.1.1)式马上得到
x+y+z=h。
这表明,不管P在△ABC内什么位置,它到三边距离之和,总等于△ABC的高。
解决这个问题就用到这一点几何知识:三角形面积等于底乘高的一半。这是小学生也知道的。有些初中几何教本,曾把这个问题编成一道习题。看来,那位经济学家和他所问的数学专家,已把小学和初中学过的这点东西忘光了。
还有这么一个问题,它极简单,却曾使一些具有相当数学素养的解题能手一时不知所措。
一块正方形的生日蛋糕(严格地说,是正四棱柱形的。因为这个正四棱柱的高相对较小,通常叫做方形蛋糕),表面上涂了薄薄一层美味的奶油,要均匀地分给5个孩子,该怎么分呢?
困难在于,不但要把体积分成5等份,同时表面积也要分成5等份。
也许你会想到:要是4个人分或8个人分就好了。不然,换成是圆形蛋糕或五星形蛋糕也好了。偏偏是方形蛋糕5个人来分!
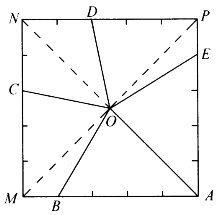
图5-2
先别抱怨!冷静地想一下,你会发现“方形”和“5个人来分”这两个条件,并没有给你增加什么困难。解法是出人意料的简单。只要找出正方形的中心——也就是两条对角线的交点O,再把正方形的每条边5等分,如图5-2,分别取等分点A、B、C、D、E,并把它们与中心O连成线段OA、OB、OC、OE。我们只要沿这些线段向蛋糕垂直下刀就可以了。
道理呢?只要用“三角形面积等于底乘高的一半”,算一算图5-2中的三角形的面积就知道了。设正方形边长为a,则AB=AE=![]() ,BM=PE=
,BM=PE=![]() ,MC=PD=
,MC=PD=![]() ,CN=DN=
,CN=DN=![]() ,而O到各边距离都是
,而O到各边距离都是![]() ,于是(www.chuimin.cn)
,于是(www.chuimin.cn)

再用熟知的公式算算备块的体积,便知这种分法确实没错。
刚进入初中的孩子,从这种类型的题目中会惊奇地发现,原来他们所熟悉的三角形面积公式竟能派上这样的用场!这个平凡公式的巧妙运用,会使他们兴致盎然地进入几何大花园。
如果用a、b、c表示三角形的三边长,用ha、hb、hc,分别表示三边上的高,则三角形的面积为

从这个简单的等式,我们便能看出。
(1)若三角形两边相等,则这两边上的高也相等。
(2)若三角形两边上的高相等,则这两边也相等。
(3)若三角形两边不相等,则较大的边上的高较小。
这些都是极好的练习。它使初学者初步体会到,如何运用面积来研究几何图形的性质。
但是,我们不宜从这个面积公式出发来展开平面几何。从这个公式出发,逻辑上会有一个很大的缺口。因为如果这样,我们就不但承认了在中学阶段难以严格证明的矩形面积公式,而且也承认了矩形→平行四边形→三角形的等积变形过程。这里面包含了平行公理、全等三角形等基本几何知识,要承认的东西未免太多。
我们退一步,从三角形面积公式的一个推论出发来展开,这个推论是“同高三角形面积比等于底之比”。把它作为我们的主要逻辑起点,可以避免提及“高”或者“底”这些词。因为这涉及高线的定义、存在、唯一性等问题,未免太复杂了。相比之下,我们宁可采用一条形式上较弱,叙述起来也较简单的命题:
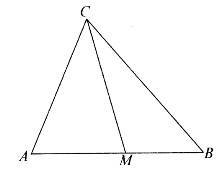
图5-3
基本命题 如图5-3,设△ABC的AB边上有一点M。如果有AM=λAB,则△AMC=λ△ABC,即
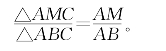
一粒小小的种子能长成参天的大树。让我们看看,这个简单的命题,如何幻化出万紫千红的几何花园吧!
有关从数学教育到教育数学的文章

在这封信中,从幼时的见面与传闻,到战争年代的四处流浪,与生活、与命运抗争,含辛茹苦抚养子女,谢觉哉以姜一生命历程中的几个片段,向我们解释了这位平凡的劳动女性不平凡的一生,让人肃然起敬。信中所叙述的姜一的遭遇正是旧中国妇女命运的缩影,具有极高的社会史料价值。在这些背景之下,谢觉哉笔下姜一的形象也逐渐丰满、高大起来。......
2023-12-03

如果你觉得分别记忆这三种状态的解法比较麻烦,下面再介绍一种只需要记忆一个公式,且完全不需要考虑UFR角块方向的方法。这6种状态中,黄绿红角块3次位于UFR位置,3次位于DFR位置,而且恰好包含了该角块在这两个位置上所有可能的状态。此时就需要整体转动魔方,将该角块移动到DFR位置,再做一次公式2-1,用位于UFR位置的角块将它替换到U层。......
2023-11-18

1956年,美国心理学家米勒教授发表了一篇重要的论文《神奇的数字7±2:我们信息加工能力的局限》,明确提出短时记忆的容量为7±2,即一般为7,并在5到9之间波动。不是的,这恰恰是神奇“7±2”存在的另一个奇特的现象。但不论人们储存的组块是什么,短时记忆的容量均为7±2个组块。这个7±2法则告诉我们一......
2023-08-07

成事高手无一不讲究借力,借力方法颇多,软硬兼施,是有心机者最善于用的借力方式。胡雪岩的妙计的第一部分,原来就是软硬兼施中的“硬”,先吓一下他,使他渐渐软下来。也就是说,胡雪岩与王有龄先硬、后软、后又硬,那位蒋老板自然是招架不住,所以蒋老板的无奈与胡雪岩坐收渔利的情形对比鲜明,所以,在收服别人的时候可以适当采取软硬兼施的办法,因为这是治人的有效策略。......
2023-12-02

3.计算分区地表水量平衡公式城市计算分区(地表水):式中:CRWt、CLWt、CXWt分别为水库对城市供水量、城市当地可供水量以及外流域或区域对城市供水量;CDt、CIt、CAt、CEt、COt分别为城市生活用水、城市工业用水、城市农业用水、城市生态环境用水和城市其他用水;CETt、CFTt分别为城市蒸发、城市渗漏水量;CRWt为城市退水;CCWt为城市重复利用水量。......
2023-06-30

在参与教研活动的过程中,教师深入研究教材、研究学生、研究教法,促进了教师的专业化成长。因此,在操作中,他们遇到了困难,有些地方不会做,影响了完成的效果。本课最终被选为省级优课。我期待在我的教研路上,采撷更多亮丽的花朵,装点人生的希望田野,用我平凡的教师、教研之路,成就孩子们不平凡的人生。......
2023-11-16

解析函数不仅有一阶导数,而且有各高阶导数,它的值也可以用函数在边界上的值通过积分来表示.但是对于一元实函数来说,它在某一区间上可导,其导数在这区域上是否连续也不一定,更不要说它有高阶导数存在了.关于解析函数的高阶导数我们有下面的定理.定理2 解析函数f(z)的导数仍为解析函数,它的n阶导数为其中C为在函数f(z)的解析区域D内围绕z0 的任何一条正向简单闭曲线,而且它的内部全含于D.证明 设z0为......
2023-10-30
相关推荐