为底的对数——自然对数。若用曲线y＝下的面积引入自然对数lnx，则显得简单具体、直观性强，而且涉及的基础知识少，还把平面几何、解析几何与高等数学更密切地联系起来了。推论6.3.3对任意λ＞0，有①也可不用压缩变换，直接用求导方法证明sx1＝sλxλ。至此，可以引入自然对数了。定义6.3.2对0＜x＜+∞，记＝lnx，并称函数y＝lnx为x的自然对数。从两个定义及三个推论中，立刻得到自然对数的一系列性质。......
2023-10-17
数学教育：应用面积公式解题，从浅入深
【摘要】：[例4.4.1]试证明在△ABC中，若∠A＝∠B，则a＝b。用面积公式代入：由AB＝AC，即得sinα＞sinβ。[例4.4.3]在△ABC中，已知a＞b，求证：∠A＞∠B。由式得a＝b，这与假设a＞b矛盾。图4-22[例4.4.4]如图4-22，设△ABC中∠A的平分线为AP，求证：。[例4.4.6]已知△ABC中的∠A和b、c两边，求∠A的角平分线长。可见在AP⊥BC时取到最大值。由AB＝CD，得sin∠APE＝sin∠DQE。
在目前各种通用几何教材中，三角形面积公式
是一个微不足道的小角色。但当我们起用它之后，会发现这个“小角色”是那样重要——它几乎担当起逻辑体系中心的重任。事实表明，平面几何的几乎全部信息，都浓缩在这个平凡的公式里了。
值得注意的是，这个小小的公式不但是平面几何中逻辑推理的基础，同时也是直接参与解题的有力工具。把它与“三角形内角和定理”配合起来，能解决大量的平面几何问题。引进这个公式之后，即使在逻辑上暂不继续展开，也会使学生们大开眼界，对几何学习产生浓厚的兴趣。
我们用例题来说明这个公式的广泛应用。
[例4.4.1] 试证明在△ABC中，若∠A＝∠B，则a＝b。
证明：因为△ABC＝
acsinB＝
bcsinA，
故
于是由sinA＝sinB得a＝b。
这是一个很平常的题目，但这种证法比用全等三角形方法利落得多。
[例4.4.2] 若0°≤β＜α，且α+β＜180°，求证：
sinβ＜sinα
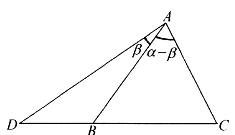
图4-21
证明：如图4-21，△ABC是顶角为α－β的等腰三角形。由α+β＜180°，可在底边CB延长线上取一点D，使∠DAB＝β，则△DAC＞△DAB。用面积公式代入：
由AB＝AC，即得sinα＞sinβ。
锐角正弦的递增性是一条重要性质。不少教材中仅仅是描述了这条性质，这里用面积法给出一个直观而严谨的证明。
[例4.4.3] 在△ABC中，已知a＞b，求证：∠A＞∠B。
证明：用反证法。如果∠A＞∠B不成立，则∠A≤∠B。以下分∠A＝∠B、∠A＜∠B两种情形讨论。
若∠A＝∠B，则sinA＝sinB。由（4.4.1）式得a＝b，这与假设a＞b矛盾。
若∠A＜∠B，∠A+∠B＜180°，用例4.4.2的结果，得sinA＜sinB，由（4.4.1）式得a＜b，与假设a＞b矛盾。
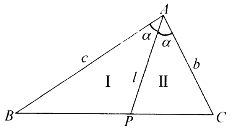
图4-22
[例4.4.4] 如图4-22，设△ABC中∠A的平分线为AP，求证：
。
证明：利用三角形面积公式得：
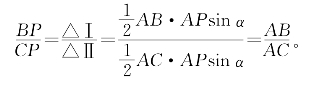
[例4.4.5] 设0°＜α＜90°，求证：sin2α＝2sinα·sin（90°－α）。
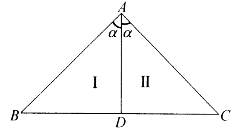
图4-23
证明：如图4-23，等腰三角形ABC的顶角A为2a，∠A的平分线为AD，由△ABC＝△Ⅰ+△Ⅱ得：
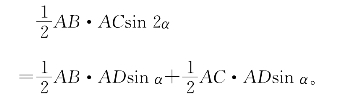
利用AB＝AC以及AD＝ABsinB＝ABsin（90°－α），代入整理即得。
[例4.4.6] 已知△ABC中的∠A和b、c两边，求∠A的角平分线长。
解：利用图4-23，用面积公式代入等式△ABC＝△Ⅰ+△Ⅱ，并设角平分线AP之长为l，则
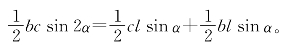
这里α＝
，将sin2α＝2sinαsin（90°－α）代入，即可解出
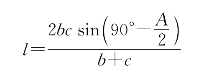
或者写成
用公式（4.4.2）很容易推出著名的司坦纳—雷米欧斯定理：有两条相等的角平分线的三角形是等腰三角形。事实上，若△ABC中∠A和∠B的角平分线同为l，由（4.4.2）式可得：
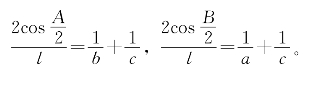
两式相减得
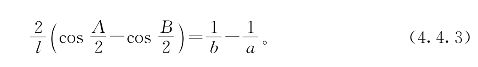
若a与b不相等，不妨设a＞b，则∠A＞∠B，于是（4.4.3）式左端为负而右端为正，矛盾。
前面几个例子比较简单，但面积公式并非不能帮我们解决较难的问题。
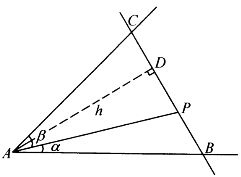
图4-24
[例4.4.7] （美国1979年数学奥林匹克竞赛题）如图4-24，在∠A内有一定点P，过P作直线交两边于B、C，问
何时取到最大值？
解：在BC上取D使AD⊥BC，并设AD＝h，S1、S2分别表示△ABP和△ACP的面积。
根据面积公式得：
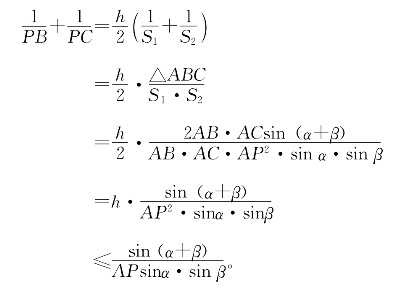
因为P是∠A内的定点，所以AP、α、β都是常数，因而上式最后一项
是常数，即永远有
而当AP⊥BC时，AD与AP重合，即h＝AP，这里的不等式取到了等号。可见
在AP⊥BC时取到最大值。
[例4.4.8] 在△ABC的两边AB、AC上，分别向外作正方形ACGH和BAFE。延长BC边上的高DA，交FN于M。求证：
MH＝MF。
证明：如图4-25，可能有两种情形：①D在线段BC上；②D在CB的延长线上。下面的证明适用于这两种情形。
一方面，显然有∠MAH＝∠ACB，∠MAF＝∠ABC。记α＝∠MAH，β＝∠MAF。于是
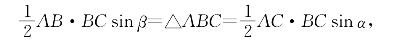
故
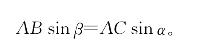
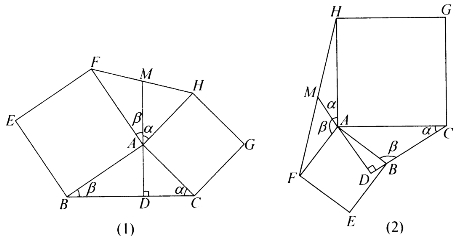
图4-25
而
即
[例4.4.9] 在凸四边形ABCD中，已知AB＝CD，E、F分别是AD和BC的中点。延长AB、DC分别和EF的延长线交于P、Q。求证：∠APE＝∠DQE。
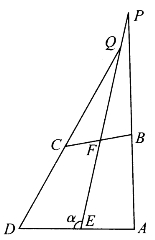
图4-26
证明：如图4-26，记α＝∠OED，则
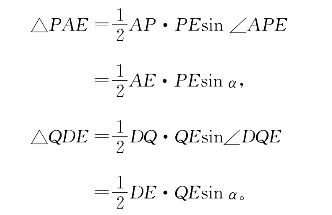
两式相比
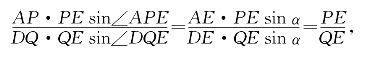
所以(www.chuimin.cn)
同理
用（4.4.4）式减（4.4.5）式得
ABsin∠APE＝CDsin∠DQE。
由AB＝CD，得sin∠APE＝sin∠DQE。
此题另一简单证法，可参看例题5.3.20。
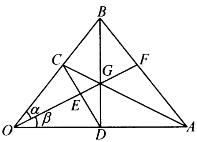
图4-27
[例4.4.10] 如图4-27，凸四边形ABCD的两边AD、BC延长后交于O，对角线AC、BD交于G。直线OG分别交CD、AB于E、F，求证：
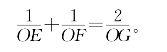
证明：设AO＝a，BO＝b，CO＝c，DO＝d，GO＝g，EO＝e，FO＝f，∠AOF＝β，∠BOF＝α。因为
△AOF+△BOF＝△AOB，
所以
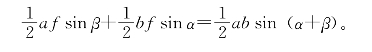
两端同除以
abf得
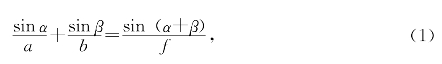
同理
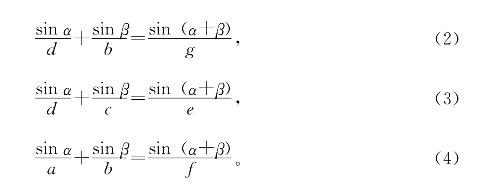
（1）－（2）+（3）－（4）得
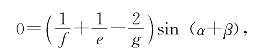
由此可得所要证明的
。
这个例题的结论可以改写成
＝2，即
，也就是
＝
。这在图上是
，即G、O按等比内外分EF。这是射影几何的一个基本定理。
此题另一证法，参看例题5.3.12。
新加坡大学的李秉彝教授，曾向笔者提出一个小问题：能不能用面积方法直接证明当0≤γ≤x≤
时，不等式sinx－sinγ≥（x－y）cosx成立，这里x，y均为弧度数。下面给出回答：
[例4.4.11] 若0≤y≤x≤
，则
sinx－siny≥（x－y）cosx。
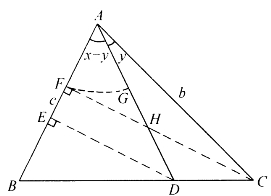
图4-28
证明：如图4-28，设△ABD是等腰三角形，∠BAD＝x－y，AB＝AD＝c。在BD的延长线上取一点C使得∠CAB＝x，则∠CAD＝y。设DE、CF分别是△ABD、△ABC的高。H是AD、CF的交点，再以A为圆心，AF为半径作弧，交AD于G。由△ABC－△ADC＝△ABD得
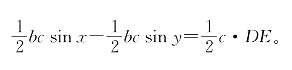
所以
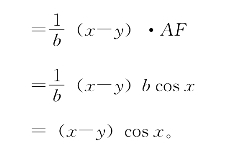
下面的例子表明，面积方法有时能帮助我们解决相当困难的问题。
在《牛顿力学的横向研究》一书中，作者查有梁教授提到了他发现的一个计算圆锥曲线曲率的简单公式。设圆锥曲线的极坐标方程式为r＝ 
，又设α是曲线上某点A处的切线与该点关于极点的向径所成的夹角，则A点的曲率半径为ρ＝
。
这个公式大大优于传统公式。查教授曾告诉笔者，他多年寻求这一公式的初等证明而未获成功。在这里，我们就用面积方法给出上述公式的一种证明。
[例4.4.12] 设圆锥曲线Γ在极坐标系（θ，r）中的方程式为r＝
，α是Γ上某点A处的切线与该点关于极点的向径所成的夹角，则Γ在A点的曲率半径为ρ＝psin－3α。
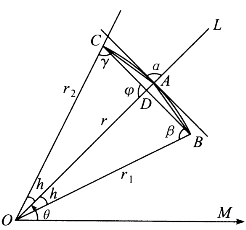
图4-29
证明：图4-29画出了圆锥曲线Γ的一部分。极坐标的极点为O，极轴为OM。曲线Γ的方程式为r＝r（θ），A、B、C是Γ上的3个点，并且有∠BOA＝∠AOC＝h。又设OA＝r，OB＝r1，OC＝r2，OA与BC交于D。分别以a、b、C记△ABC的3条边BC、CA、AB；而∠AOM、∠BOM、∠COM、∠ADB、∠ABO、∠ACO顺次记作θ、θ－h、θ+h、φ、β、γ，则有r＝r（θ），r1＝r（0－h），r2＝r（θ+h）等等。
设△ABC的外接圆半径为ρ（θ，h），则Γ在A处的曲率半径ρ（θ）＝
）。
而ρ（θ，h）可由△ABC的面积及其3边长来确定，也就是有
由
又由
△OBC＝△OBD+△OCD，
得
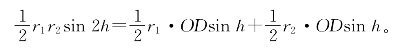
把sin2h＝2sinhcosh代入后得到
再利用
得
把式（2）、（3）、（4）代入式（1），令h趋近于0得
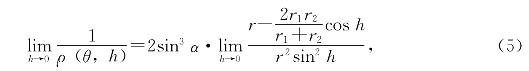
再利用Γ的方程式得
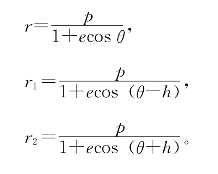
代入（5）式取极限可得
此即所求公式。
我们看到，一个平凡的三角形面积公式，它的变化是无穷的。几何图形里总有若干个三角形，把这些三角形的面积用不同的方法来表示，就会得到许多等式。我们适当选取这些等式，推导、整理后就能获得所要的结论。
这一节里提供的展开平面几何推理体系的方案有许多好处，比如：
（1）发展迅速，学生可以较快把握住一些最重要的工具。
（2）中心明确，逻辑结构清晰。
（3）解题方法易于掌握。这是因为充分运用了三角与代数的方法。
（4）提前引入三角函数，解决了目前初中生学习三角时间过于短促，不能很好消化的问题。
但是，这个体系也有它不可忽视的问题：
（1）三角形面积公式是直观引入的，逻辑上留下了较大的缺口，要依赖旧的体系。
（2）解题几乎处处离不开三角，几何的风格丧失太多，不易被人们接受。
（3）正弦概念的提前引入，是否适应学生的年龄特征，值得商榷。
下面提供另一个方案，针对以上这些问题作出更细致的处理。
【注释】
[1]为简便，我们用记号△ABC同时表示△ABC的面积。
有关从数学教育到教育数学的文章
- 详细阅读
-
从数学教育到教育数学：连续归纳法应用详细阅读
有了连续归纳法，数学分析里的一系列涉及实数连续性和连续函数性质的定理，就可以用统一的模式来证明。以下用连续归纳法证明：这将推出每个实数都是{bn}的下界，即得矛盾。由连续归纳法，px对一切x成立。[例8.3.6]设f在[a，b]上连续，f＜0，f＞0，则至少有一个点x0∈（a，b），使f＝0。[例8.3.7]若f在[a，b]上连续，则f在[a，b]上取到最大值和最小值。......
2023-10-17
-
教育数学：评价、解题方法与成果详细阅读
对比之下，后者宽度较大，因而教师知道了前一种证法后，均乐于放弃传统教材中的方法。除了逻辑结构简单之外，能否提供有力的解题方法，也是评价教育数学成果优劣的一条重要标准。数学的心脏是问题。于是，这个任务落在了“教育数学”的肩上。充分发挥正迁移的作用，这个想法贯穿着我们在教育数学领域所做的初步工作。......
2023-10-17
-
更先进的数制-从数学教育到教育数学详细阅读
之所以说十进制并非尽善尽美，我们有更有力的理由：因为还有比十进制记数法更优越的方法。充分利用这5个指头，能造出更好的记数法来。这种记数法的好处，不仅在于少用了6，7，8，9这4个数码，更重要的是运算起来方便。比方说，3.68在新记数法里是，截尾之后得到，恰好是3.7，相当于把3.68最后的8进上去。可见，十进制记数法虽然是一份珍贵的遗产，同时也是沉重的负担。因为世界上已经有太多的人学会了现在通行的十进制记数法。......
2023-10-17
-
泰勒公式及应用数学基础篇详细阅读
【主要内容】1.带拉格朗日型余项的泰勒公式设函数f（x）在[a，b]上具有直到n阶的连续导数，在（a，b）内具有n+1阶导数，则对x0∈[a，b]，有（x∈[a，b]）.（1）其中，余项，ξ是介于x0与x之间的实数）.设函数f（x）在（a，b）上具有直到n+1阶导数，则对x0∈（a，b），有其中，余项，ξ是介于x0与x之间的实数）.式（1）和式（2）称为f（x）按（x-x0）的幂展开的带拉格朗日型......
2023-10-27
-
从数学教育到教育数学：揭示华丽转换详细阅读
数学面貌的大变化对数学教育提出了新的要求。改革数学教育的浪潮，席卷了世界所有发达国家。数学教育已经成为一门受到广泛重视的学科。数学教育学的对象是数学教学，而不是数学本身。于是，数学教育学要靠数学提供材料。为了数学教育的需要，对数学成果进行再创造，这已不是数学教育学的任务了。这主要是数学工作者的责任，是数学的任务。......
2023-10-17
-
实用性与应用：张角公式在数学教育中的价值详细阅读
下面我们将举出一些例题，它们会极有力地表明张角公式的广泛用途。由正弦定理可知代入张角公式得再利用τ＝β+γ，即得要证等式。下面举出恒等式的一个应用。[例5.6.4]设在正△ABC外接圆的上任取一点P，PA交BC于D。证明：如图5-49，∠α＝∠β＝60°，由张角公式得因为sin120°＝sin60°，即得所求。[例5.6.6]设直角三角形ABC斜边AB上的高为CD，求证：图5-51证明：如图5-51，由张角公式可得又sin（α+β）＝sin90°＝1，代入，即得所求。......
2023-10-17
-
数学教育中的余面积与勾股差详细阅读
基于余面积及勾股差的概念，我们可以把勾股定理的古希腊证法推广为余弦定理的一个证法。这时有图6-25以及由此解出这就证明了以勾股定理为特款的余弦定理。由定义及前面推出的余面积公式，可得到勾股差的基本性质勾股差PABC＝0的充分必要条件是：两点A、B重合，或B、C重合，或∠ABC为直角。[例6.5.1]已知△ABC的三边a、b、c，求此三角形面积。[例6.5.3]如图6-29，设△ABC的两高AD与CE交于H，求证：BH⊥AC。......
2023-10-17
相关推荐