之所以说十进制并非尽善尽美，我们有更有力的理由：因为还有比十进制记数法更优越的方法。充分利用这5个指头，能造出更好的记数法来。这种记数法的好处，不仅在于少用了6，7，8，9这4个数码，更重要的是运算起来方便。比方说，3.68在新记数法里是，截尾之后得到，恰好是3.7，相当于把3.68最后的8进上去。可见，十进制记数法虽然是一份珍贵的遗产，同时也是沉重的负担。因为世界上已经有太多的人学会了现在通行的十进制记数法。......
2023-10-17
从数学教育到教育数学：深入探索一个开门见山的体系
【摘要】：定义4.3.1 边长为1，有一个角为α的菱形的面积，叫做角α的正弦，记作sinα＝Sα。命题4.3.1在△ABC中，设BC＝a。把三角形面积公式各项同除以，立刻得到：正弦定理 在任意△ABC中，有这个定理的用处之大是众所周知的。在式中，我们取α+β＝90°，可立刻得到重要的命题。这样，为“余角的正弦”创设一个新符号将十分方便，余弦应运而生：定义4.3.2一个角α的余角的正弦，叫做α的余弦，记作cosα。
小学生都知道，矩形面积等于长乘宽，即S＝ab。这个公式是由图4-13直观得到的。
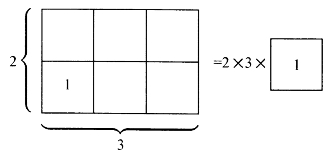
图4-13
设想上图是用木条和钉子做成的框架。一不小心，框架变斜了（如图4-14），于是矩形变成了平行四边形，小正方形变成了小菱形，面积公式也就变成了如下形式：
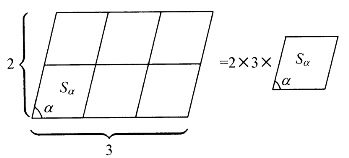
图4-14
图中的Sα代表一个边长为1、夹角为α的小菱形的面积，我们所要讲的这个体系，就靠这个小菱形起家。
定义4.3.1 边长为1，有一个角为α的菱形的面积，叫做角α的正弦，记作sinα＝Sα。当α为0°或180°时，sinα＝0。
用这种办法，我们可以单刀直入地引入正弦三角函数的直观定义。虽然这样定义有点古怪，但用起来很方便。由于把正弦规定为一个确定的面积，而不是难以捉摸的“比”，这个定义就会容易理解一些。
按定义，我们马上可以导出正弦函数的基本性质。
正弦基本性质1 对于0°≤α≤180°，sinα有定义且非负，仅当α＝0°或α＝180°时，才有sinα＝0。
正弦基本性质2 sin90°＝1。
这是因为，按定义，sin90°不过是边长为1的正方形的面积。如果按现行的定义，用直角三角形的边比来定义正弦，sin90°＝1是一个颇难理解的性质。
正弦基本性质3 sinα＝sin（180°－α）。
理由是菱形中有两角互补，而按定义，sinα和sin（180°－α）恰好是同一个菱形的面积。
这后两条基本性质可以直观地用图4-15表示出来。
图4-15
将图4-14与长方形面积公式的直观推导作类比，可以得到平行四边形面积公式。
平行四边形面积公式 若平行四边形ABCD中∠A＝α，AB＝a，AD＝b，则平行四边形面积为
▱ABCD＝AB·ADsinA＝absinα。
把任意三角形看成半个平行四边形，就有了一个三角形面积公式。
三角形面积公式 对任意△ABC，有
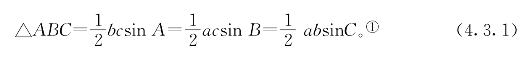
① 按惯例，我们用小写字母a、b、c顺次表示△ABC中A、B、C三个角的对边之长。
别小看这个公式，它可是我们几何新城市的交通中心呢！
为什么选它做中心？第一，平面几何里有三个最重要的度量：长度、角度和面积，这个公式把三者联系起来了；第二，三角形是平面几何的基本图形，所以这个公式处处能用；第三，这个公式还可以有广义的解释，有丰富的内涵。
这最后一点可以用下面两个命题来说明。
命题4.3.1 在△ABC中，设BC＝a。在直线BC上任取一点P，设AP＝b*，AP与BC所成角为C*（锐角或钝角任取其一），则有
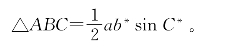
证明：如图4-16，有三种情形。情形（1）可用三角形面积公式：
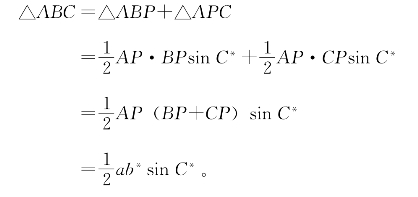
图4-16
至于情形（2），可用
△ABC＝△APC－△APB
推导。情形（3）可由
△ABC＝△ABP－△ACP
推出。
命题4.3.1通常叫做斜高公式。线段AP叫做△ABC在BC边上的一条斜高。
我们进一步考虑：如果P点不在直线BC上，那又有什么结论呢？
命题4.3.2 设ABPC是对边互不相交的四边形，对角线BC＝a，AP＝b*。直线AP与BC的交角（锐角或钝角任取其一）及交点都记为C*，则有四边形ABPC的面积
证明：如图4-17，此题分成凸四边形和凹四边形两种情形。凸四边形可用等式
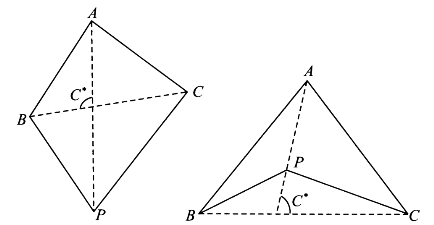
图4-17
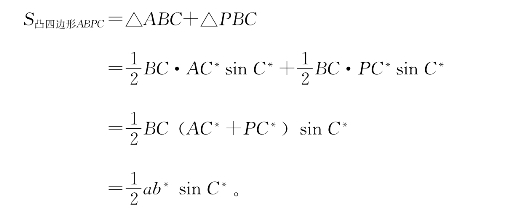
至于凹四边形，可用等式
作类似的推导。
现在，让我们从交通中心出发，迅速到达几个重要的车站。把三角形面积公式（4.3.1）各项同除以
，立刻得到：
正弦定理 在任意△ABC中，有
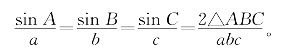
这个定理的用处之大是众所周知的。在我们这个系统中，起步之后两三个逻辑环节就得到了它。
在公式（4.3.1）中取∠C＝90°，利用sinC＝1，便得：
命题4.3.3 在△ABC中，若∠C＝90°，则
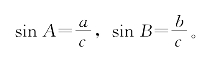
这表明，我们定义的正弦和通常用直角三角形的边比所定义的正弦是一致的。不过，我们同时还给出了钝角的正弦定义。
为了充分发挥正弦的作用，正弦加减法定理被及时引入。
命题4.3.4 当0°≤β≤α≤90°时，有正弦加法定理和正弦减法定理成立：
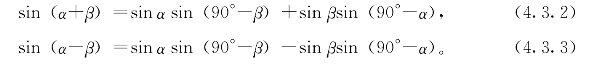
证明：如图4-18，设∠BAD＝α，∠CAD＝β，AD⊥BC，由△ABC＝△Ⅰ+△Ⅱ，并用三角形面积公式代入，得
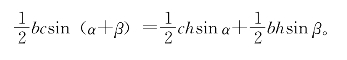
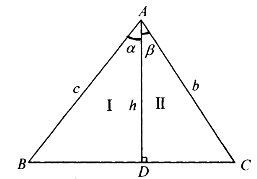
图4-18
两端同除以
，得
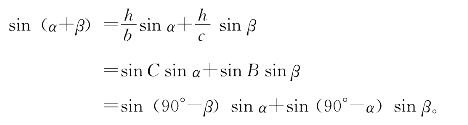
这就证明了（4.3.2）式。
要想得到正弦减法定理，来看图4-19的情形。这里△Ⅰ＝△APC－△BPC，∠APC＝α，∠BPC＝β，则有：
图4-19
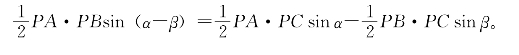
两边同除以
PA·PB，得
即（4.3.3）式。
通常教材上证明正弦和角公式时，不仅方法复杂难记，而且限制α+β≤90°。这里仅要求α、β分别不超过90°；如超过，式中出现的90°－α、90°－β便没有意义了。
在（4.3.2）式中取α＝β＝30°，便得
sin60°＝sin30°·sin60°+sin30°·sin60°，
由此解出
又取α＝β＝45°，得
解出
再取α＝30°，β＝60°，则有
将sin30°＝
代入后得
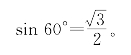
几个特殊角的正弦值便轻而易举地得到了。
在（4.3.2）式中，我们取α+β＝90°，可立刻得到重要的命题。
正弦的勾股关系 若α+β＝90°，则(www.chuimin.cn)
sin2α+sin2β＝1，
或简单地写作
再利用命题4.3.3，又得到了
勾股定理 在直角三角形ABC中，斜边的平方等于另两边平方之和，即a2+b2＝c2。
我们从（4.3.2）、（4.3.3）、（4.3.4）中看到：当研究一个角α的正弦时，不可避免地要牵涉另一个角90°－α的正弦，而α与90°－α互为余角。这样，为“余角的正弦”创设一个新符号将十分方便，余弦应运而生：
定义4.3.2 一个角α的余角的正弦，叫做α的余弦，记作cosα。具体地约定
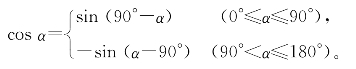
这样，我们给0°到180°之间的α角定义了余弦。有了余弦，正弦加法定理和减法定理就可以写成众所周知的形式了：
而正弦的勾股关系也可以写成
勾股关系 sin2α+cos2α＝1。
从（4.3.5）式出发，可以建立余弦和差定理、正弦与余弦的和差化积公式、倍角公式、半角公式等一套三角恒等式。
至于正切和余切，当然可以用正弦和余弦之比来定义。在必要时（例如做有关圆的切线的计算时），随时可以做这件事。
重要的是还得建立余弦定理。当然，有了勾股定理，这是很容易的。但是，我们能不能借助于面积关系，给出不依赖勾股定理的更直接的证明呢？下面就提供两种方法。在第六部分的第5小节中，将给出另一种证法。
余弦定理 在任意△ABC中，有恒等式
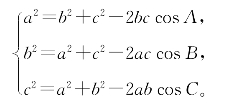
证明：只要证明三个等式中的一个就可以了。
请看图4-20（1），△ABC是具有钝角或直角C的三角形。让△ABC绕顶点C顺时针旋转一个角度α，使α＝∠C，会出现和它全等△A′B′C。设直线AB与A′B′交于D，注意到∠1＝∠2、∠A＝∠A′，故有∠ADA′＝∠C。
从图4-20（1）直接可以看出
△BCB′+△ACA′+△BCA′＝△BB′A′+△AB′A′。
利用三角形面积公式，上式可写成
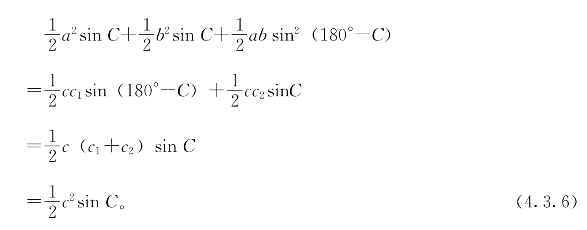
利用二倍角公式（正弦加法定理取α＝β可得）
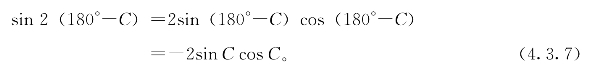
把（4.3.7）式代入（4.3.6）式，两边同除以
sinC，即得
当C为锐角时，如图4-20（2），有
△BCB′+△ACA′－△BCA′＝△BB′A′+△AB′A′。
如法炮制，不再赘述。
这样证明余弦定理，好处是直观性强，把余弦定理中的每一项都用面积表示出来了，而且允许勾股定理成为特例。
如果让△ABC绕C点旋转90°，也可以证出来，而且不用倍角公式，也不用同除以sinC。如图4-21（1），△ABC中∠C≥90°。注意到∠1＝∠2、∠A＝∠A′，故AB⊥A′B′，于是
△BA′B′+△AA′B′＝△BCB′+△ACA′+△BCA′+△ACB′。
记D为AB、A′B′交点，使用三角形面积公式后得
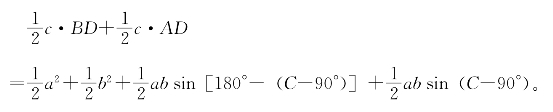
整理后两边乘2，就是
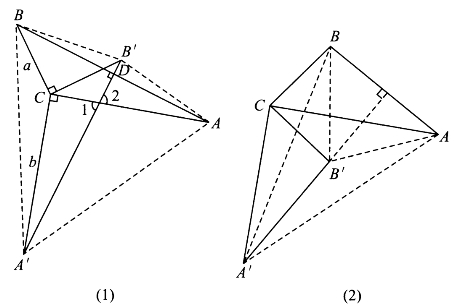
图4-20
锐角情形如图4-20（2）。△ABC中∠C为锐角，让△ABC绕C顺时针旋转90°，得△A′B′C′。这时
△BA′B′+△AA′B′＝△BCB′+△ACA′－△BCA′－△ACB′，
使用面积公式并加以整理，可得到同样结果。
上面用了相当长的篇幅，介绍余弦定理的证法。其实“醉翁之意不在酒”，目的是想要说明面积方法的灵活运用。如果仅仅为了证明余弦定理，就连图也不必画。事实上，对△ABC有：
再利用正弦定理，可知有正数k，
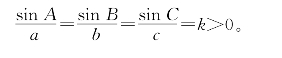
代入（4.3.8）式，约去k，即得余弦定理。
这种证法，用到了正弦加法定理和余弦加法定理，正弦与余弦之间的勾股关系以及正弦定理。其优点是具有代数的简洁性与普遍性。
对比之下，图4-21的证法所要求的预备知识最少。
有了正弦定理和余弦定理，欧氏体系中的基本工具——全等三角形与相似三角形的判定定理唾手可得。虽然这些判定定理在我们的体系中所起的作用不大，但可作为辅助工具。
全等三角形的判定
（1）（边、边、边） 设△ABC与△A′B′C′的3边对应相等，即a＝a′，b＝b′，c＝c′，则△ABC≌△A′B′C′。
证明：只要证明∠A＝∠A′，∠B＝∠B′，∠C＝∠C′就可以了。用余弦定理得
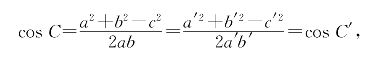
这表明∠C＝∠C′。同理∠A＝∠A′，∠B＝∠B′。
（2）（边、角、边） 在△ABC与△A′B′C′中，若a＝a′，b＝b′，∠C＝∠C′，则△ABC≌△A′B′C′。
证明：由余弦定理可知
c2＝a2+b2－2abcosC＝a′2+b′2－2a′b′cosC′＝c′2，
故c＝c′。再用“边、边、边”判定法。
（3）（角、边、角） 已知在△ABC与△A′B′C′中，∠A＝∠A′，∠B＝∠B′，c＝c′，则△ABC≌△A′B′C′。
证明：显然∠C＝∠C′。由正弦定理
两式相比得
由c＝c′，便知a＝a′和b＝b′。
（4）（角、角、边） 略。
相似三角形的判定
（1）（边、边、边） 若△ABC和△A′B′C′的对应边成比例，则△ABC∽△A′B′C′。
证明：设
，则
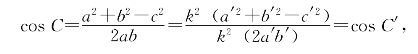
于是∠C＝∠C′。同理∠A＝∠A′，∠B＝∠B′。
（2）（边、角、边） 若△ABC和△A′B′C′有一对对应角相等，且此角的夹边对应成比例，则△ABC∽△A′B′C′。
证明：设∠C＝∠C′，且
＝k，则
故得
即知两三角形相似。
（3）（角、角） 若△ABC与△A′B′C′有两对对应角相等，则△ABC∽△A′B′C′。
证明：设∠A＝∠A′，∠B＝∠B′，则∠C＝∠C′。由正弦定理
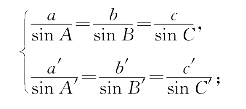
两式相比得即知两三角形相似。
至此为止，平面几何里最基本的部分——三角形的研究，已经粗具规模了。
我们以上进行的推理，逻辑结构是比较简单的。基本出发点是两条：
一条是三角形面积公式△ABC＝
absinC。它是用直观类比的方法从矩形面积公式演变而来的。这个演变过程是不严密的，但在获得了所要的公式之后，进一步的推演便是一板一眼的了。
另一条是三角形内角和为180°。我们在推导正弦加法定理和余弦定理时用到它，推导全等三角形和相似三角形的判定定理也用到它，将来推导圆周角定理还要用到它。这是一条重要的基本定理，可以从三角形面积公式推出来。这一点，我们将在下一节论述。但是，也许直接承认“平行线的同位角判定法”，在教育实践中更为可取，正如目前中学几何教材中所做的那样。
逻辑结构图示如下：
有关从数学教育到教育数学的文章
- 详细阅读
-
从数学教育到教育数学：揭示华丽转换详细阅读
数学面貌的大变化对数学教育提出了新的要求。改革数学教育的浪潮，席卷了世界所有发达国家。数学教育已经成为一门受到广泛重视的学科。数学教育学的对象是数学教学，而不是数学本身。于是，数学教育学要靠数学提供材料。为了数学教育的需要，对数学成果进行再创造，这已不是数学教育学的任务了。这主要是数学工作者的责任，是数学的任务。......
2023-10-17
-
面积与自然对数：从数学教育到教育数学详细阅读
为底的对数——自然对数。若用曲线y＝下的面积引入自然对数lnx，则显得简单具体、直观性强，而且涉及的基础知识少，还把平面几何、解析几何与高等数学更密切地联系起来了。推论6.3.3对任意λ＞0，有①也可不用压缩变换，直接用求导方法证明sx1＝sλxλ。至此，可以引入自然对数了。定义6.3.2对0＜x＜+∞，记＝lnx，并称函数y＝lnx为x的自然对数。从两个定义及三个推论中，立刻得到自然对数的一系列性质。......
2023-10-17
-
从数学教育到教育数学：连续归纳法应用详细阅读
有了连续归纳法，数学分析里的一系列涉及实数连续性和连续函数性质的定理，就可以用统一的模式来证明。以下用连续归纳法证明：这将推出每个实数都是{bn}的下界，即得矛盾。由连续归纳法，px对一切x成立。[例8.3.6]设f在[a，b]上连续，f＜0，f＞0，则至少有一个点x0∈（a，b），使f＝0。[例8.3.7]若f在[a，b]上连续，则f在[a，b]上取到最大值和最小值。......
2023-10-17
-
从数学教育到教育数学，逻辑展开与平行线定理详细阅读
命题5.4.1设M、N两点在直线AB的同侧，则MN∥AB的充分必要条件是△MAB＝△MAB。这是上一小节已证明的例题5.3.9。命题5.4.2两直线AB、CD和另一直线l交于P、Q，若同位角相等，则AB∥CD。于是，共角比例定理可以完善成为命题5.4.4若△ABC与△A′B′C′中，有∠A＝∠A′或∠A+∠A′＝180°，则。命题5.4.5PQ∥AB，若直线l与AB垂直，则l也和PQ垂直。推论5.4.2平行线处处等距。推论5.4.3若直线l1∥l2，而l3与l1、l2相截，则内错角相等。......
2023-10-17
-
不使用ε-语言，讨论数列极限|从数学教育到教详细阅读
定义7.3.3设{an}是无穷数列。用“ε-语言”，不仅能够引入极限概念，还能证明与极限有关的一系列基本定理，直接计算一些具体的极限。实践证明确实有效，而且比用“ε-语言”还要简便！[例7.3.1]求证数列是无穷小列。有些微积分的参考资料以此题为例，说明不用“ε-语言”不可能严格地讲微积分。命题7.3.1设{αn}、{βn}为无穷小列，{Ln}为有界数列。......
2023-10-17
-
从数学教育到教育数学，解析函数极限新方法详细阅读
既然讲数列极限可以不用“ε-语言”，那么讲函数极限也可以不用“ε-语言”，只不过用“无界不减函数”代替“无界不减数列”罢了。定义7.4.2设f是在[c，+∞）上有定义的函数。用“ε-语言”讲函数极限，常常要一条一条分别给出各种过程中的极限定义。这一套定义，将使学生在学习微积分时免受“ε-语言”之累，在定理证明和做题时用代数运算代替逻辑推理。[例7.4.1]求证：＝+∞。......
2023-10-17
-
点到面推理：数学教育到教育数学详细阅读
前面的几个例子都有这个特点：利用一点邻域的性质来推出全局的性质。抓住这一点，便能建立一个统一的推理模式，使许多定理的证明简化。我们引入一个“可分命题”的概念。可分命题 设命题Q△是涉及区间△的一个判断，如果满足下面两条：若Q△成立，且△1△，则Q△成立。使用定理Q，一定要把所要证的命题设法转化成一个有关的可分命题。下面，我们用上一节的例题来说明这种推理模式的用法。推证方法同确界存在定理，用反证法。......
2023-10-17
相关推荐