首页理论教育面积计算：了解多面手的数学原理

面积计算：了解多面手的数学原理

2025-09-30 理论教育版权反馈

【摘要】：如图4-8，半径为的圆的面积恰为4，即等于正方形ABCD的面积。当然，一个角域的面积正好等于一个弓形域的面积。一眼就能看出，扇形的面积小于△OAD而大于△OAB。在高等数学中，面积以各种形式出现。面积是积分，是测度，是外微分形式，是向量的外积，也是行列式。抓住面积，结合代数与三角来展开初等几何，就极有希望提供一种比传统几何教材更易学、更生动丰富的几何教材，提供一种足以和欧几里得体系争夺课堂的几何教材。

请看图4-4，它直观地说明了恒等式

（a+b）2＝a2+2ab+b2。

pagenumber_ebook=29,pagenumber_book=17

图4-4

pagenumber_ebook=29,pagenumber_book=17

图4-5

而图4-5，则生动地告诉了我们另一个有用的恒等式

x2－y2＝（x+y）（x－y）。

不是吗？大正方形x2去掉小正方形y2，得到两个梯形。每个梯形的面积恰好是（x+y）（x－y）。图4-6则明明白白地列出恒等式

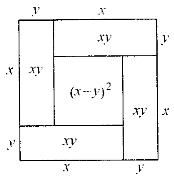
pagenumber_ebook=30,pagenumber_book=18

图4-6

（x+y）2－（x－y）2＝4xy。

因为（x－y）2≥0，顺便还得到不等式

（x+y）2≥4xy。

化简后就是非常有用的不等式

x2+y2≥2xy。

刚才这几个例子比较初等，所以你也许会想，面积只能用来表示那些最简单的关系吧！现在看看图4-7，一块阶梯形面积分成几个竖直的矩形，它的面积表示为

a1b1+a2b2+a3b3+a4b4。

pagenumber_ebook=30,pagenumber_book=18

图4-7

如果分成几个水平的矩形，就成了

pagenumber_ebook=30,pagenumber_book=18

也就是说，

pagenumber_ebook=31,pagenumber_book=19

这不正是数学分析里研究级数时常用的“阿贝尔变换恒等式”吗？

熟悉高等数学的读者，不妨再来看看下面这个难度更大的例子。这是一道研究生入学试题。

题：求证不等式

pagenumber_ebook=31,pagenumber_book=19

我们容易想到把要证的不等式两边平方，转换成一个等价的不等式

pagenumber_ebook=31,pagenumber_book=19

这里只要画出图来，问题便迎刃而解。如图4-8，半径为的圆的面积恰为4，即等于正方形ABCD的面积。不等式左边是函数 pagenumber_ebook=31,pagenumber_book=19 在圆域上的积分，而右边是同一个函数在正方形域ABCD上的积分。正方形有4个角域在圆外，而圆有4个弓形在正方形之外。当然，一个角域的面积正好等于一个弓形域的面积。因为函数关于x2+y2递增，所以角域上的函数值至少是 pagenumber_ebook=31,pagenumber_book=19 ，而弓形域上函数值至多是。至此，水落石出。

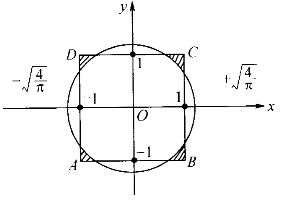
pagenumber_ebook=31,pagenumber_book=19

图4-8

面积还能用来说明三角恒等式或三角不等式。例如图4-9便说明了和化积恒等式：

pagenumber_ebook=32,pagenumber_book=20

pagenumber_ebook=32,pagenumber_book=20

图4-9

道理是这样的：设等腰三角形的顶角A＝α+β，腰长为1，底边上的高AD为h。在底边上取一点M，连接AM，设AM＝l，并使

∠BAM＝α，∠MAC＝β。(https://www.chuimin.cn)

不妨设α≥β，

pagenumber_ebook=32,pagenumber_book=20

一方面，△ABC的面积^[1]是：

pagenumber_ebook=32,pagenumber_book=20

另一方面，

pagenumber_ebook=32,pagenumber_book=20

由（4.2.2）与（4.2.3），便可得恒等式（4.2.1）。

pagenumber_ebook=33,pagenumber_book=21

图4-10

图4-10中，OA是以O为圆心的单位圆的半径，AD是这个单位圆的切线，OD交圆D于B。一眼就能看出，扇形的面积小于△OAD而大于△OAB。若用x表示∠AOB的弧度，有

pagenumber_ebook=33,pagenumber_book=21

而扇形的面积是，于是马上得到不等式：

pagenumber_ebook=33,pagenumber_book=21

这个不等式一般被用来推导重要的极限

pagenumber_ebook=33,pagenumber_book=21

pagenumber_ebook=33,pagenumber_book=21

图4-11

如果说不等式sinx＜x＜tanx太普通的话，我们再来看一个较不平凡的不等式。

题：如果0＜x2＜x1＜，求证：

pagenumber_ebook=33,pagenumber_book=21

图4-11就是这个不等式的解释。设直角三角形OAC中∠A＝90°，∠COA＝x1。在AC上取B，∠BOA＝x2。以O为圆心，OB为半径作圆，交OC于D，交OA的延长线于E，则得

pagenumber_ebook=33,pagenumber_book=21

在解析几何里，面积也能帮上忙。

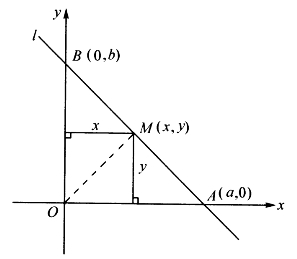
pagenumber_ebook=34,pagenumber_book=22

图4-12

图4-12画的是直角坐标系里的一条直线l，它交x、y轴于A（a，0）和B（0，b）。取l上一点M（x，y），有

△OBM+△OAM＝△OAB，也就是

pagenumber_ebook=34,pagenumber_book=22

两边同时除以，得到

这不就是l的“截距式”吗？

用不着列举更多的例子了。

利用面积，我们可以建立面积坐标，自然地进入解析几何。而面积坐标，本质上已包含了笛卡儿坐标、仿射坐标、射影坐标，这就为学习更高深的几何埋下了伏笔。

学会了计算多边形和圆的面积，自然会想到去计算曲线包围的图形的面积。这就会引出极限概念，引出定积分概念，自然而然地就把学生带进了高等数学的大门。此外，微积分里用得最多的三角函数与对数函数（指数函数），都可以用面积给出易于理解又便于推导的定义。

在高等数学中，面积以各种形式出现。面积是积分，是测度，是外微分形式，是向量的外积，也是行列式。

抓住面积，从小学到大学的数学内容就可以一线相串。抓住面积，结合代数与三角来展开初等几何，就极有希望提供一种比传统几何教材更易学、更生动丰富的几何教材，提供一种足以和欧几里得体系争夺课堂的几何教材。

丰富的素材有了，主题思想有了，现在需要的就是具体的结构。