1）产业政策分析产业政策是由政府制定和实施的旨在提高资源在产业及企业间的配置效率，促进并优化本国产业发展及经济增长的经济政策。在进行产业结构政策分析时，应重点关注政府对主导产业的选择以及对幼小产业的扶持。产业技术政策分析产业技术政策是指政府所制定的用以引导和干预产业技术进步的政策。这一行业因经济增长而获得丰厚的利润，因经济衰退而蒙受损失。......
2025-09-29
面积法：古老的证题工具为你带来新视角
【摘要】：几何学的产生，源于人们对土地面积的测量需要。而且，面积很早就成为人们认识几何图形性质与证明几何定理的工具。勾股定理的证法，多达300余种。细心的读者会发现：把图4-1沿虚线剪掉一半，中国的古老证明就变成了加菲尔德的证明！从勾股定理的这几个证法，可以归纳出面积方法的一个基本模式：用不同的办法求出同一块面积，得到一个等式，再从这个等式推出所要的结论。
几何学的产生，源于人们对土地面积的测量需要。这样的故事已经为人所熟知：在古埃及，尼罗河每年要泛滥一次。洪水给两岸的田地带来了肥沃的淤积泥土，但也抹掉了田地之间的界线标志。水退了，人们要重新画出田地的界线，就必须再次丈量、计算田地的面积。年复一年，人们就积累了最基本的几何知识。
这样，几何学从一开始便与面积结下了不解之缘。就连英语中的几何“Geometry”的字头“geo－”，也含有“土地”之意。而且，面积很早就成为人们认识几何图形性质与证明几何定理的工具。
勾股定理，这个被誉为“几何的基石”的重要定理，它的被发现与被证明，不管是在中国，还是在古希腊，都与面积有关。
勾股定理说：在直角三角形中，两直角边的平方之和等于斜边的平方。而我国古代把直角三角形较短的直角边叫“勾”，较长的直角边叫“股”，斜边叫“弦”。于是，勾股定理便被叙述为：勾方加股方等于弦方。这也是勾股定理名称的由来。
勾股定理的证法，多达300余种。一个最古老的精彩证法，出自我国古代无名数学家之手。我们不妨来鉴赏一下：
勾股定理证法之一
如图4-1，4个同样大小的直角三角形的斜边，围成了一个正方形。它们的直角边，围成了一个更大的正方形。（为什么？）
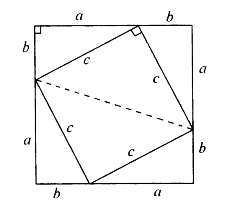
图4-1
由题意，大正方形面积
S1＝（a+b）2，
小正方形面积
S2＝c2，
而直角三角形面积
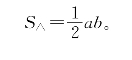
当然有
S1＝S2+4S△，
即
（a+b）2＝c2+2ab
展开整理之后，便得a2+b2＝c2。
这种证明方法影响很广，变种极多。下面只介绍两个有趣而简捷的证法。(https://www.chuimin.cn)
勾股定理证法之二
把两本大小一样的书，一横一竖并排放在一起，像图4-2那样。
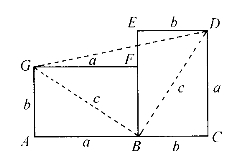
图4-2
一方面，梯形ACDG的面积，按梯形面积公式来算应当是
另一方面，这个梯形可以分割成3个三角形：△ABG、△BCD、△GBD。我们注意到∠GBD是直角，便知道这3个三角形的面积顺次是
。因而得到
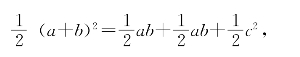
整理一下，便是a2+b2＝c2。
这个证法是美国第20届总统加菲尔德的杰作。细心的读者会发现：把图4-1沿虚线剪掉一半，中国的古老证明就变成了加菲尔德的证明！
从图4-2的“两本书”还可以演化出一个更简捷的证明。
勾股定理证法之三
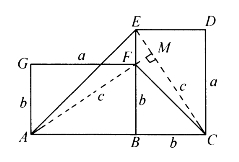
图4-3
如图4-3，凹四边形ACFE可以分割成两个等腰直角三角形：△ABE和△FBC。两者的面积分别是
和
，即
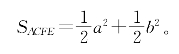
另一方面，这个四边形又可以分割成△AFE和△AFC。前者面积等于
AF×EM，后者面积等于
AF×MC，这是因为直线AF⊥CE（为什么？），而点M是垂足。所以
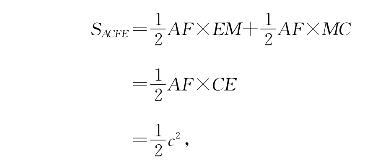
立刻导出a2+b2＝c2。
从勾股定理的这几个证法，可以归纳出面积方法的一个基本模式：用不同的办法求出同一块面积，得到一个等式，再从这个等式推出所要的结论。这很像列方程式解应用题。面积，把几何与代数沟通起来了。
相关文章
- 详细阅读
-
堆积条形图、折线图和面积图工具简介详细阅读
在Illustrator CS6的工具箱中有9种图表类型。这种图表类型适合用于表示部分和总体的关系。这种图表类型通常适用于表示在一段时间内一个或多个主题的趋势。图10-4 堆积条形图工具图10-5 折线图工具图10-6 面积图工具8.饼图工具使用饼图工具可以创建圆形的图表，图表的楔形用于比较数值的相对比例，如图10-8所示。这种图表类型也称为网状图。......
2025-09-30
-
先进分析工具：优化你的数据分析详细阅读
Spectre支持跟踪电路分析和模拟，通过简单的界面化电路模拟操作，可以让设计者快速掌握电路设计，节约大量学习和设计仿真参数的时间。Spectre还提供多种高阶的电路模拟工具，如Parametric Analysis、Corner Analysis、Monte Carlo Analysis、RF Analysis。Monte Carlo AnalysisMonte Carlo Analysis可以帮助设计者针对多种参数以概率分布的方式来随机抽样来做模拟，并以统计图表的方法呈现。设计者可以利用Monte Carlo Analysis分析结果，以其统计的角度预先做良率分析，优化设计，以提高生产良率。......
2025-09-29
-
教师的儿童研究引论: 为你呈现真实成果详细阅读
以前述的“教师的儿童研究”的本质反观我国当下教师的儿童研究，不得不承认，我国教师的儿童研究现状堪忧，尤其是在过度奉行速度和效率的学校中更是如此。这种控制主要体现在教师的儿童研究的取向上。有鉴于此，我国当下的教育界亟待反思和超越“诊断”取向的儿童研究。教师的儿童研究主要存在两类模仿，即模仿大学研究者和模仿校内外的同行。......
2025-09-29
-
如何持续搭讪话题？超级搭讪学为你解答！详细阅读
估计很多人都会说：“最大的挑战就是怎样才能够和对方一直聊得兴致勃勃。”那么，怎样才能够在搭讪成功之后保持持续的交谈呢？当和对方成功搭上话之后，你可以将周边的事物作为切入点来展开话题。当你把谈话的重点放在周边的环境上时，就可以轻易地把话题转移到与环境相关的事物上来。这样的话，当谈话告一段落时，双方才会对彼此都有所了解。......
2025-09-29
-
唐代巧妙的木偶制作工艺：《木偶》为你呈现详细阅读
唐代木偶戏所用的偶形及其制作工艺都已经非常成熟，有的木偶装置今天看来也是相当神奇的，甚至不可思议。有一篇唐传奇叫《马待封》，里面介绍了当时的巧匠马待封制作木偶的故事。领命以后，马待封一心扑在木人上，废寝忘食地进行研制。唐高宗限定他三个月内交货，误期重处。第二天早朝，群臣议完国事后，唐高宗召马待封入朝受封。唐高宗向群臣宣布说：“巧匠马待封制造木人有功，朕……”......
2025-09-29
-
食品制作，餐法与工具：完整指南详细阅读
此犁杆之另一端，则安以弓背形之横木，约有胸部宽，其凹面向上，是为把胸部放在其间，工作得力。一种是用牛力的犁，与云南汉人所用者相同，但较简单。犁架是以木杆一个，与地平行，其一端镶以铁制之三角形犁板，尖略向下。此种牛用的犁式，当是受汉人的影响，但用人力的犁，却是傈僳特有的。原傈僳是耕山地的，山坡倾斜不平，石砾甚多。此两种碓式，后一个，即手碓，是傈僳固有的。......
2025-09-30
-
宝宝爱辅食：为你准备健康、营养的食物详细阅读
我记住了你发出的第一声妈妈，我的眼睛立刻湿润，感动浸润全身。我洗手做羹汤，研究最科学的育儿方法，为你精心准备健康，营养又可口的食物。我希望你有洁净的身体，健康的体魄。我知道你所吃的每一口食物都将成长为你的一部分，为此我殚精竭虑。谨以此书，送给唯唯。萨巴蒂娜，于2018年的北京萨巴蒂娜：国内畅销美食图书出版人、主编。曾出版美食小说《厨子的故事》，美食散文集《美味关系》。......
2025-09-29
相关推荐