数学面貌的大变化对数学教育提出了新的要求。改革数学教育的浪潮，席卷了世界所有发达国家。数学教育已经成为一门受到广泛重视的学科。数学教育学的对象是数学教学，而不是数学本身。于是，数学教育学要靠数学提供材料。为了数学教育的需要，对数学成果进行再创造，这已不是数学教育学的任务了。这主要是数学工作者的责任，是数学的任务。......
2023-10-17
更先进的数制-从数学教育到教育数学
【摘要】：之所以说十进制并非尽善尽美，我们有更有力的理由：因为还有比十进制记数法更优越的方法。充分利用这5个指头，能造出更好的记数法来。这种记数法的好处，不仅在于少用了6，7，8，9这4个数码，更重要的是运算起来方便。比方说，3.68在新记数法里是，截尾之后得到，恰好是3.7，相当于把3.68最后的8进上去。可见，十进制记数法虽然是一份珍贵的遗产，同时也是沉重的负担。因为世界上已经有太多的人学会了现在通行的十进制记数法。
不过，不同数制的转换也不是什么了不得的困难，在计算机里，略施小技，就能解决十进制到二进制的转换问题。之所以说十进制并非尽善尽美，我们有更有力的理由：因为还有比十进制记数法更优越的方法。
两只手有10个指头，一只手可只有5个指头。中国算盘里上珠以一代五，大大方便了运算。充分利用这5个指头，能造出更好的记数法来。
比方说，我们可以删除6，7，8，9这4个数码，只留下0，1，2，3，4，5（要知道，关于7，8，9的加减乘除，正是一年级小学生觉得最难的）。仍然是十进制，但记数时加减并用。一个数码顶上画一杠表示减去它。具体来说，0，1，2，3，4，5的写法不变。数码6没有了，但因为6＝10－4，所以6可以写成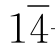
——十位上的1代表10，个位上的
代表负4。照此处理，7写成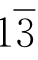
，8写成12，9写成11，而10还是10。从11到15照旧，而16到19则变成了
、
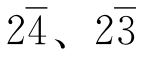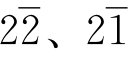。类似地，27是
，81是
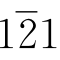，97是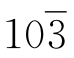
，104仍是104，7267则变成1
。
这种记数法的好处，不仅在于少用了6，7，8，9这4个数码，更重要的是运算起来方便。
有人详细总结了这种记数法的好处，大致有以下六条：
（1）基本的加减法容易多了，因为只剩下5以内的加减法。
（2）乘法表的内容大大减少。如果不算1的乘法，就只有10句。
（3）学会加法也就学会了减法。例如：
(www.chuimin.cn)
这样，代数里的正负数加减法就融合在算术运算里了。
（4）由于正负抵消，连续相加变得更容易了。比较一下这两个算式，可见一斑：左边的老式算法，由于不能正负相消，每一竖列相加时都涉及较多的运算。
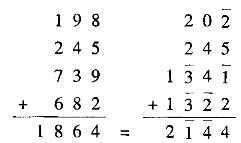
（5）加减混合运算可以在一个竖式里进行。
（6）四舍五入的规则没有了，取而代之的是简单的“截尾”。比方说，3.68在新记数法里是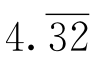
，截尾之后得到
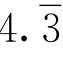，恰好是3.7，相当于把3.68最后的8进上去。而3.64是
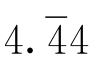，截尾之后是
，即3.6。
想一想，单是简化乘法表，就能使孩子们提前半个学期学会乘法。此外，由于记数法本身和正负号紧密地联系在一起，还可以使代数变得更容易。
可见，十进制记数法虽然是一份珍贵的遗产，同时也是沉重的负担。初学算术的孩子，也许会有最深刻的体会吧！
尽管早在1726年，已有人提出以上介绍的这种加减记数法（就在这一年，英国人约翰·科尔森向英国皇家学会介绍了这个系统），但还是太晚了。因为世界上已经有太多的人学会了现在通行的十进制记数法。要改，将涉及整个社会，要遇到不可克服的阻力，要付出巨大的代价。
有关从数学教育到教育数学的文章
- 详细阅读
-
面积与自然对数：从数学教育到教育数学详细阅读
为底的对数——自然对数。若用曲线y＝下的面积引入自然对数lnx，则显得简单具体、直观性强，而且涉及的基础知识少，还把平面几何、解析几何与高等数学更密切地联系起来了。推论6.3.3对任意λ＞0，有①也可不用压缩变换，直接用求导方法证明sx1＝sλxλ。至此，可以引入自然对数了。定义6.3.2对0＜x＜+∞，记＝lnx，并称函数y＝lnx为x的自然对数。从两个定义及三个推论中，立刻得到自然对数的一系列性质。......
2023-10-17
-
从数学教育到教育数学：连续归纳法应用详细阅读
有了连续归纳法，数学分析里的一系列涉及实数连续性和连续函数性质的定理，就可以用统一的模式来证明。以下用连续归纳法证明：这将推出每个实数都是{bn}的下界，即得矛盾。由连续归纳法，px对一切x成立。[例8.3.6]设f在[a，b]上连续，f＜0，f＞0，则至少有一个点x0∈（a，b），使f＝0。[例8.3.7]若f在[a，b]上连续，则f在[a，b]上取到最大值和最小值。......
2023-10-17
-
从数学教育到教育数学，逻辑展开与平行线定理详细阅读
命题5.4.1设M、N两点在直线AB的同侧，则MN∥AB的充分必要条件是△MAB＝△MAB。这是上一小节已证明的例题5.3.9。命题5.4.2两直线AB、CD和另一直线l交于P、Q，若同位角相等，则AB∥CD。于是，共角比例定理可以完善成为命题5.4.4若△ABC与△A′B′C′中，有∠A＝∠A′或∠A+∠A′＝180°，则。命题5.4.5PQ∥AB，若直线l与AB垂直，则l也和PQ垂直。推论5.4.2平行线处处等距。推论5.4.3若直线l1∥l2，而l3与l1、l2相截，则内错角相等。......
2023-10-17
-
不使用ε-语言，讨论数列极限|从数学教育到教详细阅读
定义7.3.3设{an}是无穷数列。用“ε-语言”，不仅能够引入极限概念，还能证明与极限有关的一系列基本定理，直接计算一些具体的极限。实践证明确实有效，而且比用“ε-语言”还要简便！[例7.3.1]求证数列是无穷小列。有些微积分的参考资料以此题为例，说明不用“ε-语言”不可能严格地讲微积分。命题7.3.1设{αn}、{βn}为无穷小列，{Ln}为有界数列。......
2023-10-17
-
从数学教育到教育数学，解析函数极限新方法详细阅读
既然讲数列极限可以不用“ε-语言”，那么讲函数极限也可以不用“ε-语言”，只不过用“无界不减函数”代替“无界不减数列”罢了。定义7.4.2设f是在[c，+∞）上有定义的函数。用“ε-语言”讲函数极限，常常要一条一条分别给出各种过程中的极限定义。这一套定义，将使学生在学习微积分时免受“ε-语言”之累，在定理证明和做题时用代数运算代替逻辑推理。[例7.4.1]求证：＝+∞。......
2023-10-17
-
点到面推理：数学教育到教育数学详细阅读
前面的几个例子都有这个特点：利用一点邻域的性质来推出全局的性质。抓住这一点，便能建立一个统一的推理模式，使许多定理的证明简化。我们引入一个“可分命题”的概念。可分命题 设命题Q△是涉及区间△的一个判断，如果满足下面两条：若Q△成立，且△1△，则Q△成立。使用定理Q，一定要把所要证的命题设法转化成一个有关的可分命题。下面，我们用上一节的例题来说明这种推理模式的用法。推证方法同确界存在定理，用反证法。......
2023-10-17
-
从数学教育到教育数学：深入探索一个开门见山的详细阅读
定义4.3.1 边长为1，有一个角为α的菱形的面积，叫做角α的正弦，记作sinα＝Sα。命题4.3.1在△ABC中，设BC＝a。把三角形面积公式各项同除以，立刻得到：正弦定理 在任意△ABC中，有这个定理的用处之大是众所周知的。在式中，我们取α+β＝90°，可立刻得到重要的命题。这样，为“余角的正弦”创设一个新符号将十分方便，余弦应运而生：定义4.3.2一个角α的余角的正弦，叫做α的余弦，记作cosα。......
2023-10-17
相关推荐