首页理论教育坐标系与参数方程，高考数学全国卷，套路揭秘

坐标系与参数方程，高考数学全国卷，套路揭秘

2023-10-15 理论教育版权反馈

【摘要】：续表考点1：坐标系1.（2017全国II，22）在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρcosθ=4.（1）M为曲线C1上的动点，点P在线段OM上，且满足|OM||OP|=16，求点P的轨迹C2的直角坐标方程；（2）设点A的极坐标为（2，），点B在曲线C2上，求△OAB面积的最大值.考点2：参数方程2.（2017全国I，22）在直角坐标系xOy

续表

考点1：坐标系

1.（2017全国II，22）在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρcosθ=4.（1）M为曲线C1上的动点，点P在线段OM上，且满足|OM||OP|=16，求点P的轨迹C2的直角坐标方程；

（2）设点A的极坐标为（2，），点B在曲线C2上，求△OAB面积的最大值.

考点2：参数方程

2.（2017全国I，22）在直角坐标系xOy中，曲线C的参数方程为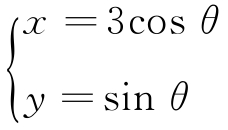（θ为参数），直线l的参数方程为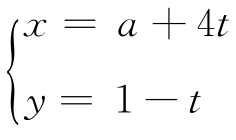（t为参数）.

（1）若a=-1，求曲线C与l的交点坐标；

（2）若曲线C上的点到l距离的最大值为，求a.

1.以直角坐标系的原点O为极点，x轴正半轴为极轴，并在两种坐标系中取相同的长度单位，已知直线l的参数方程为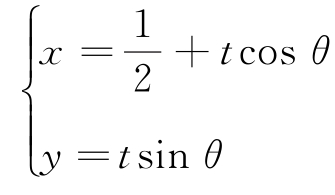，（t为参数，0＜θ＜π），曲线C的极坐标方程为ρsin2α-2cosα=0.

（1）求曲线C的直角坐标方程；

（2）设直线l与曲线C相交于A，B两点，当θ变化时，求|AB|的最小值.

2.已知椭圆（φ为参数），A，B是C上的动点，且满足OA⊥OB（O为坐标原点），以原点O为极点，x轴的正半轴为极轴建立极坐标系，点D的极坐标为（4，）.

（1）求线段AD的中点M的轨迹E的普通方程；

（2）利用椭圆C的极坐标方程证明+为定值，并求△AOB面积的最大值.

3.已知曲线C的极坐标方程为ρ-4cosθ=0，以极点为原点，极轴为x轴正半轴建立平面直角坐标系，直线l过点M（3，0），倾斜角为.

（1）求曲线C的直角坐标方程与直线l的参数方程；

（2）设直线l与曲线C交于A，B两点，求|MA|+|MB|.

4.已知直线l的参数方程为（t为参数），以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，圆C的极坐标方程为ρ=4cos（θ-）.

（1）求圆C的直角坐标方程；

（2）若P（x，y）是直线l与圆面ρ≤4cos（θ-）的公共点，求μ=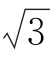x+y的取值范围.

5.在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，半圆C的极坐标方程为ρ=2cosθ，θ∈[0，].

（1）求C的参数方程；

（2）设点D在半圆C上，半圆C在D处的切线与直线l：y=3x+2垂直，根据（1）中得到的参数方程，求直线CD的倾斜角及D的坐标.

6.在直角坐标系xOy中，曲线C1的参数方程为（t为参数），在以原点O为极点，x轴正半轴为极轴（两坐标系取区间的长度单位）的极坐标系中，曲线C2：ρ=2sinθ.

（1）求曲线C1的普通方程与曲线C2的直角坐标方程；

（2）M，N分别是曲线C1和曲线C2上的动点，求|MN|最小值.

7.已知直线l的参数方程是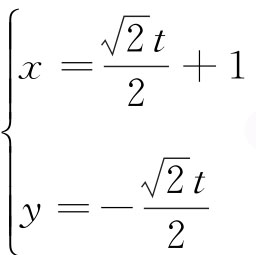（t是参数），以坐标原点为极点，x轴的正半轴为极轴，且取相同的长度单位建立极坐标系，圆C的极坐标方程为ρ=2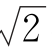cos（θ+）.(www.chuimin.cn)

（1）求直线l的普通方程与圆C的直角坐标方程；

（2）设圆C与直线l交于A，B两点，若点P的直角坐标为（1，0），求|PA|+|PB|的值.

8.在直角坐标系xOy中，曲线C的参数方程为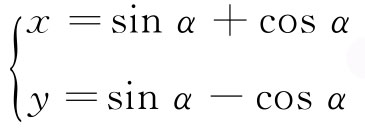（α为参数）.

（1）求曲线C的普通方程；

（2）在以O为极点，x正半轴为极轴的极坐标系中，直线l的方程为ρsin（-θ）+1=0，已知直线l与曲线C相交于A，B两点，求|AB|的值.

9.在直角坐标系xOy中，曲线C1：（t为参数，t≠0），其中0≤α＜π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，曲线C3：ρ=2cosθ.

（1）求曲线C2与C3交点的直角坐标；

（2）若曲线C2与C1相交于点A，C3与C1相交于点B，求|AB|的最大值.

10.在平面直角坐标系xOy中，以O为极点，x轴非负半轴为极轴建立极坐标系，已知曲线C的极坐标方程为ρsin2θ=4cosθ，直线l的参数方程为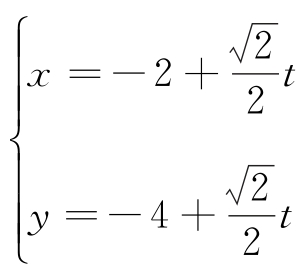（t为参数），两曲线相交于M，N两点.

（1）写出曲线C的直角坐标方程和直线l的普通方程；

（2）若P（-2，-4），求|PM|+|PN|的值.

11.（2016辽宁鞍山一模）在直角坐标系xOy中，以原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的方程为ρ=4cosθ，直线l的方程为（t为参数），直线l与曲线C的公共点为T.

（1）求点T的极坐标；

（2）过点T作直线l′，l′被曲线C截得的线段长为2，求直线l′的极坐标方程.

12.在直角坐标系xOy中，直线l的参数方程为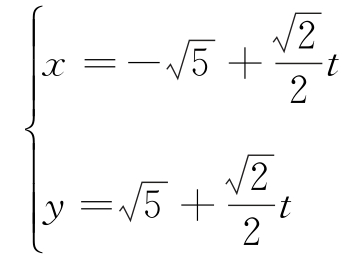（t为参数），若以O点为极点，x轴正半轴为极轴建立极坐标系，则曲线C的极坐标方程为ρ=4cosθ.

（1）求曲线C的直角坐标方程及直线l的普通方程；

（2）将曲线C上各点的横坐标缩短为原来的，再将所得曲线向左平移1个单位长度，得到曲线C1，求曲线C1上的点到直线l的距离的最小值.

13.在平面直角坐标系中，直线l的参数方程为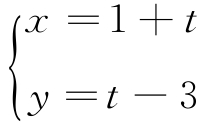（t为参数），在以直角坐标系的原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ=.

（1）求曲线C的直角坐标方程和直线l的普通方程；

（2）若直线l与曲线C相交于A，B两点，求△ABO的面积.

14.已知直线C1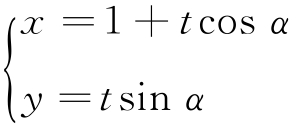：（t为参数），曲线C2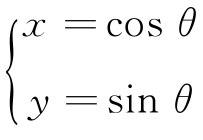：（θ为参数）.

（1）当α=时，求C1与C2交点的坐标；

（2）过坐标原点O作C1的垂线，垂足为A，P为OA中点，当α变化时，求点P轨迹的参数方程，并指出它是什么曲线.

15.在平面直角坐标系xOy中，曲线C1的参数方程为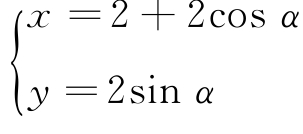（α为参数）.以O为极点，x轴正半轴为极轴，并取相同的单位长度建立极坐标系.

（1）写出C1的极坐标方程；

（2）设曲线C2：+y2=1经伸缩变换后得到曲线C3，射线θ=（ρ＞0）分别与C1和C3交于A，B两点，求|AB|的值.