首页理论教育高考数学应用题：导数在函数中的应用

高考数学应用题：导数在函数中的应用

2025-09-30 理论教育版权反馈

【摘要】：续表考点：导数在研究函数中的应用（2017全国I，21）已知函数f（x）=ae2x+（a-2）ex-x.（1）讨论f（x）的单调性；（2）若f（x）有两个零点，求a的取值范围.1.（2017山东莱芜二模）已知函数f（x）=ex[x2+（a+1）x+2a-1].（1）当a=-1时，求函数f（x）的单调区间；（2）若关于x的不等式f（x）≤ea在[a，+∞）上有解，求实数a的取值范围；（3）若曲线y=

续表

考点：导数在研究函数中的应用

（2017全国I，21）已知函数f（x）=ae2x+（a-2）ex-x.

（1）讨论f（x）的单调性；

（2）若f（x）有两个零点，求a的取值范围.

1.（2017山东莱芜二模）已知函数f（x）=ex[x2+（a+1）x+2a-1].

（1）当a=-1时，求函数f（x）的单调区间；

（2）若关于x的不等式f（x）≤ea在[a，+∞）上有解，求实数a的取值范围；

（3）若曲线y=f（x）存在两条互相垂直的切线，求实数a的取值范围.

2.已知函数f（x）=ln x+ax在点（t，f（t））处的切线方程为y=3x-1.

（1）求a的值；

（2）已知k≤2，当x＞1时，f（x）＞k（1-） +2x-1恒成立，求实数k的取值范围；

（3）对于在（0，1）中的任意一个常数b，是否存在正数x0，使得ef（x0+1）-3x0-2+x02＜1？请说明理由.

3.已知函数f（x）=-aln（x+1）+-a-1（a∈R）.

（1）讨论f（x）在（0，+∞）上的单调性；

（2）若对任意的正整数n都有（1+） n-a ＞e成立，求a的取值范围.

4.（2017四川内江五模）已知函数f（x）=xex-ln x（ln 2≈-0.693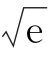， ≈1.648，均为不足近似值）.

（1）当x≥1时，判断函数f（x）的单调性；

（2）证明：当x＞0时，不等式f（x）＞恒成立.

5.已知函数f（x）=（a ∈R），曲线y=f（x）在点（1，f（1））处的切线与直线x+y+1=0垂直.

（1）试比较20162017与20172016的大小，并说明理由；

（2）若函数g（x）=f（x）-k有两个不同的零点x1，x2，证明：x1·x2＞e2.

6.（2017安徽蚌埠三模）已知f（x）=ln（ax+b）+x2（a≠0）.

（1）若曲线y=f（x）在点（1，f（1））处的切线方程为y=x，求a，b的值；

（2）若f（x）≤x2+x恒成立，求ab的最大值.

7.已知函数f（x）=ax2+2x-ln（x+1）（a为常数）.

（1）当a=-1时，求函数f（x）的单调区间；

（2）当x∈[0，+∞）时，不等式f（x）≤x恒成立，求实数a的取值范围.

8.已知f（x）=e2x-x2-a.

（1）证明f（x）在（-∞，+∞）上为增函数；

（2）当a=1时，解不等式f[f（x）]＞x；

（3）若f[f（x）-x2-2x]＞f（x）在（0，+∞）

上恒成立，求a的最大整数值.

9.（2017湖南张家界一模）已知函数f（x）=ex，g（x）=ln x+1（x≥1）.

（1）求函数h（x）=f（x-1）-g（x）（x≥1）的最小值；

（2）已知1≤y＜x，求证：ex-y-1＞ln x-ln y；

（3）设H（x）=（x-1）2f（x），在区间（1，+∞）内是否存在区间[a，b]（a＞1），使函数H（x）在区间[a，b]的值域也是[a，b]？请给出结论，并说明理由.

10.（2017安徽马鞍山三模）已知函数f（x）=ln（ax+b）+ex-1（a≠0）.(https://www.chuimin.cn)

（1）当a=-1，b=1时，判断函数f（x）的零点个数；

（2）若f（x）≤ex-1+x+1，求ab的最大值.

11.（2017湖南怀化一模）已知函数f（x）=ln x-，g（x）=（x-1）2-1.

（1）若a＞0，试判断f（x）在定义域内的单调性；

（2）若f（x）在[1，e]上的最小值为，求a的值；

（3）当a=0时，若x≥1时，恒有x·f（x）≤λ[g（x）+x]成立，求λ的最小值.

12.已知函数f（x）=（a+1）ln x-x2，g（x）=.

（1）讨论函数f（x）的单调区间；

（2）若函数f（x）与g（x）在（0，+∞）上的单调性正好相反.

①对于∀x1，x2∈[ ，3]，不等式恒成立，求实数t的取值范围；

②令h（x）=xg（x）-f（x），两个正实数x1，x2满足h（x1）+h（x2）+6x1x2=6，证明：0＜x1+x2≤1.

13.（2017江西南昌三模）已知函数f（x）=eax+bx（a＜0）在点（0，f（0））处的切线方程为y=5x+1，且f（1）+f′（1）=12.

（1）求函数y=f（x）的极值；

（2）若f（x）＞x2+3在x∈[1，m]上恒成立，求正整数m的最大值.

14.（2017山东济南二模）已知函数f（x）=ln x-ax2+ax，a∈R.

（1）当a＜0时，讨论函数f（x）极值点的个数；

（2）若关于x的不等式f（x）≤2ax-x-1恒成立，求整数a的最小值；

（3）对于函数f（x）图像上任意给定的两点A（x1，f（x1）），B（x2，f（x2）），试判断与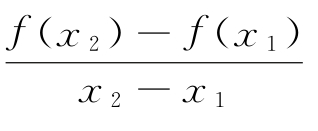的大小关系（其中f′（x）是函数f（x）的导函数），并给出证明.

15.已知函数f（x）=ax-ln x，F（x）=ex+ax，其中x＞0，a＜0，e为自然对数的底数.

（1）若f（x）和F（x）在区间（0，ln 3）内具有相同的单调性，求实数a的取值范围；

（2）若a∈（-∞，-]，且函数g（x）=xeax-1-2ax+f（x）的最小值为M，求M的最小值.

16.（2017江西九江三模）已知函数f（x）=ax（ln x-1）-x2（a∈R）恰有两个极值点x1，x2，且x1＜x2.

（1）求实数a的取值范围；

（2）若不等式ln x1+λln x2＞1+λ恒成立，求实数λ的取值范围.

17.（2017新疆二模）已知函数f（x）=.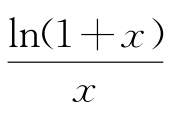

（1）试判断函数f（x）在（0，+∞）上的单调性，并说明理由；

（2）若函数f（x）在其定义域内恒有f（x）＜成立，试求a所有可能的取值集合.

18.已知函数f（x）=（1-a2）x2-ax，其中a∈R.

（1）若曲线y=f（x）在点（1，f（1））处的切线方程为8x+y-2=0，求a的值；

（2）当a≠0时，求函数f（x）（x＞0）的单调区间与极值；

（3）若a=1，存在实数m，使得方程f（x）=m恰好有三个不同的解，求实数m的取值范围.

19.函数f（x）=ln x+x2+ax（a∈R），g（x）=ex+x2.

（1）讨论f（x）的极值点的个数；

（2）若对于∀x＞0，总有f（x）≤g（x），

①求实数a的取值范围；

②求证：对于∀x＞0，不等式ex+x2-（e+1）x+＞2成立.