高考数学典题：空间直线与平面的垂直与平行

2023-10-15 理论教育版权反馈

【摘要】：若存在，求出λ=的值？

续表

考点1：点、直线、平面之间的位置关系

1.（2014全国II，18）如图，四棱锥PABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点.

（1）证明：PB∥平面AEC；

（2）设二面角D-AE-C为60°，AP=1，AD=，求三棱锥E-ACD的体积.

考点2：空间向量的应用

2.（2017全国I，18）如图，在四棱锥P-ABCD中，AB∥CD，且∠BAP=∠CDP=90°.

（1）证明：平面PAB⊥平面PAD；

（2）若PA=PD=AB=DC，∠APD=90°，求二面角A-PB-C的余弦值.

1.如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB=AC=AA1，AB⊥AC，D是棱BB1的中点.

（1）证明：平面A1DC⊥平面ADC；

（2）求平面A1DC与平面ABC所成二面角的余弦值.

2.（2017山东莱芜二模）已知四棱锥PABCD中，底面ABCD是菱形，∠BAD=60°，AB=PB=PD=2，PA=.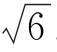

（1）求证：BD⊥PC；

（2）若E是PA的中点，求二面角A-EC-B的余弦值.

3.已知等边三角形PAB的边长为4，四边形ABCD为正方形，平面PAB⊥平面ABCD，E，F，G，H分别是线段AB，CD，PD，PC上的点.

（1）如图①，若G为线段PD的中点，BE=DF=1，证明：PB∕∕平面EFG；

（2）如图②，若E，F分别是线段AB，CD的中点，DG=3GP，CH=HP，求二面角HEF-G的余弦值.

4.（2017辽宁葫芦岛二模）如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，AP=AB=AC=a，AD=a，PA⊥底面ABCD.

（1）求证：平面PCD⊥平面PAC；

（2）在棱PC上是否存在一点E，使得二面角B-AE-D的平面角的余弦值为-？若存在，求出λ=的值？若不存在，说明理由.

5.如图所示，在三棱锥A-BCD中，侧面ABD，ACD是全等的直角三角形，AD是公共的斜边且AD=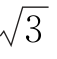，BD=CD=1，另一侧面ABC是正三角形.

（1）求证：AD⊥BC；

（2）若在线段AC上存在一点E，使ED与平面BCD成30°角，试求二面角A-BD-E的大小.

6.如图所示，在多面体ABCDE中，△BCD是边长为2的正三角形，AE∕∕DB，AE⊥DE，2AE=BD，DE=1，平面ABDE⊥平面BCD，F是CE的中点.

（1）求证：BF⊥CD；

（2）求二面角C-BF-D的余弦值.

7.如图①，在高为2的梯形ABCD中，AB∕∕CD，AB=2，CD=5，过点A，B分别作AE⊥CD，BF⊥CD，垂足分别为E，F.已知DE=1，将梯形ABCD沿AE，BF同侧折起，得空间几何体ADE-BCF，如图②.

（1）若AF⊥BD，证明：△BDE为直角三角形；

（2）若DE∕∕CF，CD=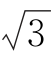，求平面ADC与平面ABFE所成角的余弦值.

8.（2017山东青岛二模）在三棱柱ABCA1B1C1中，侧面ABB1A1为矩形，AB=2，AA1=2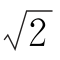，D是AA1的中点，BD与AB1交于点O，且CO⊥平面ABB1A1.

（1）证明：平面AB1C⊥平面BCD；

（2）若OC=OA，△AB1C的重心为G，求直线GD与平面ABC所成角的正弦值.

9.如图，平面ABCD⊥平面BCF，四边形ABCD是菱形，∠BCF=90°.

（1）求证：BF=DF；(www.chuimin.cn)

（2）若∠BCD=60°，且直线DF与平面BCF所成角为45°，求二面角B-AF-C的平面角的余弦值.

10.（2017山东济南二模）如图，矩形FCEB是圆柱OO1的轴截面，且FC=1，FB=2，点A，D分别在上、下底面圆周上，且在面FCEB的同侧，△OAB是等边三角形，∠ECD=60°，M，N分别是OC，AE的中点.

（1）求证：MN∕∕平面CDE；

（2）求二面角C-AD-E的余弦值.

11.（2017福建宁德三模）如图，在四棱台ABCD-A1B1C1D1中，底面ABCD为平行四边形，∠BAD=120°，M为CD上的点.且∠A1AB=∠A1AD=90°，AD=A1A=2，A1B1=DM=1.

（1）求证：AM⊥A1B；

（2）若M为CD的中点，N为棱DD1上的点，且MN与平面A1BD所成角的正弦值为，试求DN的长.

12.（2017湖南怀化一模）如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD是等腰梯形，∠ADC=120°，AB=2CD=2，平面D1DCC1⊥平面ABCD，D1C⊥AB，M是线段AB的中点.

（1）求证：D1M∕∕面B1BCC1；

（2）若DD1=2，求平面C1D1M和平面ABCD所成的锐角的余弦值.

13.已知矩形ABCD与直角梯形ABEF，∠DAF=∠FAB=90°，点G为DF的中点，AF=EF=AB=，点P在线段CD 上运动.

（1）证明：BF∕∕平面GAC；

（2）当P运动到CD的中点位置时，PG与PB长度之和最小，求二面角P-CE-B的余弦值.

14.（2017河南平顶山一模）如图，在四棱锥P-ABCD中，CB⊥平面PAB，AD∕∕BC，且PA=PB=AB=BC=2AD=2.

（1）求证：平面DPC⊥平面BPC；

（2）求二面角C-PD-B的余弦值.

15.（2017河北石家庄一模）在四棱锥SABCD中，底面ABCD为平行四边形，∠DBA=60°，∠SAD=30°，AD=SD=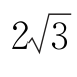，BA=BS=4.

（1）证明：BD⊥平面SAD；

（2）求二面角A-SB-C的余弦值.

16.（2017江西九江三模）如图所示，等腰梯形ABCD的底角A等于60°.直角梯形ADEF所在的平面⊥平面ABCD，∠EDA=90°，且ED=AD=2AF=2AB=2.

（1）证明：平面ABE⊥平面EBD；

（2）点M在线段EF上，试确定点M的位置，使平面MAB与平面ECD所成的角的余弦值为.

17.如图，在以A，B，C，D，E为顶点的六面体中，△ABC和△ABD均为等边三角形，且平面ABC⊥平面ABD，EC⊥平面ABC，EC=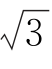，AB=2.

（1）求证：DE⊥平面ABD；

（2）求二面角D-BE-C的余弦值.

18.（2017安徽马鞍山三模）如图，在四棱柱ABCD-A1B1C1D1中，A1A⊥底面ABCD，四边形ABCD为梯形，AD∕∕BC，且AD=2BC，Q为BB1的中点，过A1，Q，D三点的平面记为α.

（1）证明：平面α与平面A1B1C1D1的交线平行于直线CD；

（2）若AA1=3，BC=CD=，∠BCD=120°，求平面α与底面ABCD所成二面角的大小.

19.如图①，在直角梯形ABCD中，AD∕∕BC，AD⊥DC，BC=2AD=2DC，四边形ABEF是正方形.将正方形ABEF沿AB折起到四边形ABE1F1的位置，使平面ABE1F1⊥平面ABCD，M为AF1的中点，如图②.

（1）求证：AC⊥BM；

（2）求平面CE1M与平面ABE1F1所成锐二面角的余弦值.

20.如图，在斜三棱柱ABC-A1B1C1中，侧面AA1B1B为菱形，底面△ABC是等腰直角三角形，∠BAC=90°，A1B⊥B1C.

（1）求证：直线AC⊥直线BB1；

（2）若直线BB1与底面ABC成的角为60°，求二面角A-BB1-C的余弦值.

高考数学典题：空间直线与平面的垂直与平行

相关推荐