高考数学全国卷：概率与统计，零件抽检与监控

续表

考点1：概率

（2017全国I，19）为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm）.根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N（μ，σ2）.

（1）假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在（μ-3σ，μ+3σ）之外的零件数，求P（X≥1）及X的数学期望；

（2）一天内抽检零件中，如果出现了尺寸在（μ-3σ，μ+3σ）之外的零件，就认为这条生产线在这一天的生产过程中可能出现了异常情况，需对当天的生产过程进行检查.

①试说明上述监控生产过程方法的合理性；②下面是检验员在一天内抽取的16个零件的尺寸：

经计算得=9.97，s=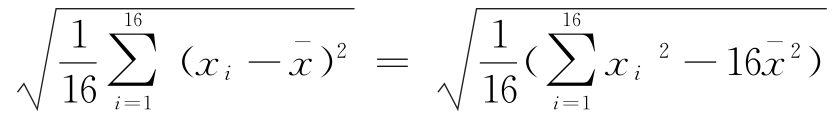≈0.212，其中xi为抽取的第i个零件的尺寸，i=1，2，…，16.

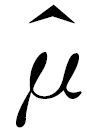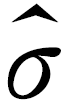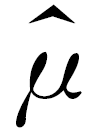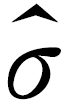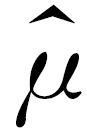用样本平均数x-作为μ的估计值，用样本标准差s作为σ的估计值，利用估计值判断是否需要对当天的生产过程进行检查.剔除（-3，+3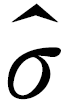）之外的数据，用剩下的数据估计μ和σ（精确到0.01）.

附：若随机变量Z服从正态分布N（μ，σ2），则P（μ-3σ＜Z＜μ+3σ）=0.9974，0.997416≈0.9592，≈00.9.

考点2：统计案例

（2017全国II，18）海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg），其频率分布直方图如下：

（1）记A表示事件“旧养殖法的箱产量低于50kg”，估计A的概率；

（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：

（3）根据箱产量的频率分布直方图，对两种养殖方法的优劣进行比较.

附：

1.（2017山东济南二模）2017年4月1日，国家在河北省白洋淀以北的雄县、容城、安新3县设立雄安新区，这是继深圳经济特区和上海浦东新区之后又一具有全国意义的新区，是千年大计、国家大事，多家央企为了配合国家战略支持雄安新区建设，纷纷申请在新区建立分公司，若规定每家央企只能在雄县、容城、安新3个片区中的一个片区设立分公司，且申请其中任一个片区设立分公司都是等可能的，每家央企选择哪个片区相互之间互不影响且必须在其中一个片区建立分公司，向雄安新区申请建立分公司的任意4家央企中：

（1）求恰有2家央企申请在雄县片区建立分公司的概率；

（2）用X表示这4家央企中在雄县片区建立分公司的个数，用Y表示在容城或安新片区建立分公司的个数，记ξ=|X-Y|，求ξ的分布列和数学期望.

2.奥运会乒乓球比赛共设男子单打、女子单打、男子团体、女子团体四种比赛，共产生四枚金牌，保守估计中国乒乓球男队单打或团体获得一枚金牌的概率均为，中国乒乓球女队单打或团体获得一枚金牌的概率均为.

（1）求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率；

（2）记中国乒乓球队获得的金牌数为ξ，按此估计ξ的分布列和数学期望E（ξ）.

3.某学校有甲、乙两个实验班，为了了解班级成绩，采用分层抽样的方法从甲、乙两个班的学生中，分别抽取8名和6名，测试他们的数学成绩与英语成绩（单位：分），用（m，n）表示.下面是乙班6名学生的测试分数：A（138，130），B（140，132），C（140，130），D（134，140），E（142，134），F（134，132），当学生的数学成绩和英语成绩满足m≥135，且n≥130时，该学生可被定为优秀学生.

（1）已知甲班共有80名学生，用上述样本数据估计乙班优秀学生的数量；

（2）从乙班抽出的上述6名学生中随机抽取3名，求至少有2名优秀学生的概率；

（3）从乙班抽出的上述6名学生中随机抽取2名，其中优秀生数记为ξ，求ξ的分布列和数学期望.

4.某学校为了制订治理学校门口上学、放学期间家长接送孩子乱停车现象的措施，对全校学生家长进行了问卷调查.根据从其中随机抽取的50份调查问卷，得到了如下的列联表.

（1）学校计划在同意限定区域停车的家长中，按照分层抽样的方法，随机抽取5人在上学、放学期间在学校门口参与秩序维持.在随机抽取的5人中，选出2人担任召集人，求至少有一名女性的概率；

（2）已知在同意限定区域停车的12位女性家长中，有3位日常开车接送孩子.现从这12位女性家长中随机抽取3人参与秩序维持，记参与秩序维持的女性家长中，日常开车接送孩子的女性家长人数为ξ，求ξ的分布列和数学期望.

5.为了研究学生的数学核心素养与抽象（能力指标x）、推理（能力指标y）、建模（能力指标z）的相关性，并将它们各自量化为1，2，3三个等级，再用综合指标w=x+y+z的值评定学生的数学核心素养；若w≥7，则数学核心素养为一级；若5≤w≤6，则数学核心素养为二级；若3≤w≤4，则数学核心素养为三级，为了了解某校学生的数学核素养，调查人员随机访问了某校10名学生，得到如下结果：

（1）在这10名学生中任选2人，求这2人的建模能力指标相同的概率；

（2）从数学核心素养等级是一级的学生中任选1人，其综合指标为a，从数学核心素养等级不是一级的学生中任选1人，其综合指标为b，记随机变量X=a-b，求随机变量X的分布列及其数学期望.

6.（2017吉林长春四模）某市对大学生毕业后自主创业人员给予小额贷款补贴，贷款期限分为6个月、12个月、18个月、24个月、36个月五种，对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元，从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计，选取贷款期限的频数如下表：

以上表中各种贷款期限的频数作为2017年自主创业人员选择各种贷款期限的概率.

（1）某大学2017年毕业生中共有3人准备申报此项贷款，计算其中恰有2人选择贷款期限为12个月的概率；

（2）设给某享受此项政策的自主创业人员补贴为X元，写出X的分布列；该市政府要做预算，若预计2017年全市有600人申报此项贷款，则估计2017年该市共要补贴多少万元.

7.某保险公司针对一个拥有20000人的企业推出一款意外险产品，每年每位职工只要交少量保费，发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种，从事三类工种的人数分布比例如图，根据历史数据统计出三类工种的赔付频率如下表（并以此估计赔付频率）.

对于A、B、C三类工种职工每人每年保费分别为a元，a元，b元，出险后的赔偿金额分别为100万元，100万元，50万元，保险公司在开展此项业务过程中的固定支出为每年10万元.

（1）若保险公司要求利润的期望不低于保费的20%，试确定保费a，b要满足的条件；

（2）现有如下两个方案供企业选择.

方案1：企业不与保险公司合作，企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工；(www.chuimin.cn)

方案2：企业与保险公司合作，企业负责职工保费的60%，职工个人负责保费的40%，出险后赔偿金由保险公司赔付.

若企业选择方案2的支出（不包括职工支出）低于选择方案1的支出期望，求保费a，b所要满足的条件，并判断企业是否可与保险公司合作.（若企业选择方案2的支出低于选择方案1的支出期望，且与（1）中保险公司所提条件不矛盾，则企业可与保险公司合作）

8.（2017吉林长春二模）为了打好脱贫攻坚战，某贫困县农科院针对玉米种植情况进行调研，力争有效地改良玉米品种，为农民提供技术支援.现对已选出的一组玉米的茎高进行统计，获得如下茎叶图（单位：cm），设茎高大于或等于180cm的玉米为高茎玉米，否则为矮茎玉米.

（1）完成2×2列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为抗倒伏与玉米矮茎有关；

（2）①按照分层抽样的方式，在上述样本中，从易倒伏和抗倒伏两组中随机选取9株玉米，设选出的易倒伏矮茎玉米株数为X，求X的分布列（概率用组合数算式表示）；

②若将频率视为概率，从抗倒伏的玉米试验田中再随机选取50株，求选出的高茎玉米株数的数学期望和方差.

（，其中n=a+b+c+d）

9.某工程设备租赁公司为了调查A，B两种挖掘机的出租情况，现随机抽取了这两种挖掘机各100台，分别统计了每台挖掘机在一个星期内的出租天数，统计数据如下表：

A型挖掘机

B型挖掘机

（1）根据这个星期的统计数据，将频率视为概率，求该公司一台A型挖掘机，一台B型挖掘机一周内合计出租天数恰好为4天的概率；

（2）如果A，B两种挖掘机每台每天出租获得的利润相同，该公司需要从A，B两种挖掘机中购买1台，请你根据所学的统计知识，给出建议应该购买哪一种类型，并说明你的理由.

10.某市一次全市高中男生身高统计调查数据显示：全市100000名男生的身高服从正态分布N（168，16）.现从某学校高三年级男生中随机抽取50名测量身高，测量发现被测学生身高全部介于160cm和184cm之间.将测量结果按如下方式分成6组：第一组[160，164]，第二组[164，168]，…，第6组[180，184]，下图是按上述分组方法得到的频率分布直方图.

（1）试评估该校高三年级男生在全市高中男生中的平均身高状况；

（2）求这50名身高在172cm以上（含172cm）的人数；

（3）在这50名身高在172cm以上（含172cm）的男生中任意抽取2人，这2人中身高排名（从高到低）在全市前130名的人数记为ξ，求ξ的数学期望.

参考数据：若ξ-N（μ，σ2），则P（μ-σ＜ξ≤μ+σ）=0.6826，P（μ-2σ＜ξ≤μ+2σ）=0.9544，P（μ-3σ＜ξ≤μ+3σ）=0.9974.

11.某省有关部门从南昌大学校企业的LED产品中抽取1000件，测量这些产品的一项质量指标值，由测量结果得到如下的频率分布直方图：

（1）求这1000件产品质量指标值的样本平均数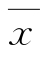和样本方差s2（同一组数据用该区间的中点值作代表）；

（2）由频率分布直方图可以认为，这种产品的质量指标值Z服从正态分布N（μ，δ2），其中μ近似为样本平均数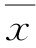，δ2近似为样本方差s2：①利用该正态分布，求P（175.6＜Z＜224.4）；②某用户从该企业购买了100件这种产品，记X表示这100件产品中质量指标值位于区间（175.6，224.4）的产品件数，利用①的结果，求E（X）.

附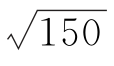：≈12.2.若Z～N（μ，δ2），则P（μ-δ＜Z＜μ+δ）=0.6826，P（μ-2δ＜Z＜μ+2δ）=0.9544.

12.为了研究家用轿车在高速公路上的车速情况，交通部门随机对50名家用轿车驾驶员进行调查，得到其在高速公路上行驶时的平均车速情况为：在30名男性驾驶员中，平均车速超过100km/h的有20人，不超过100km/h的有10人.在20名女性驾驶员中，平均车速超过100km/h的有5人，不超过100km/h的有15人.

（1）完成下面的列联表，并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关；（单位：人）

（2）以上述数据样本来估计总体，现从高速公路上行驶的大量家用轿车中随机抽取3辆，记这3辆车中驾驶员为女性且车速不超过100km/h的车辆数为ξ，若每次抽取的结果是相互独立的，求ξ的分布列和数学期望.参考公式：

K2=，其中n=a+b+c+d.参考数据：

13.为调查高中生的数学成绩与学生自主学习时间之间的相关关系，某重点高中数学教师对新入学的45名学生进行了跟踪调查，其中每周自主做数学题的时间不少于15h的有19人，余下的学生中，在学生模拟考试中数学平均成绩不足120分的占，统计成绩后，得到如下的2×2列联表：（单位：人）

（1）请完成上面的2×2列联表，并判断能否在犯错误的概率不超过0.01的前提下，认为“高中生的数学成绩与学生自主学习时间有关”；

（2）①按照分层抽样的方法，在上述样本中，从分数大于等于120分和分数不足120分的两组学生中抽取9名学生，设抽到的不足120分且周做题时间不足15h的人数是X，求X的分布列（概率用组合数算式表示）；②若将频率视为概率，从全校大于等于120分的学生中随机抽取20人，求这些人中周做题时间不少于15h的人数的期望和方差.参考公式：

K2=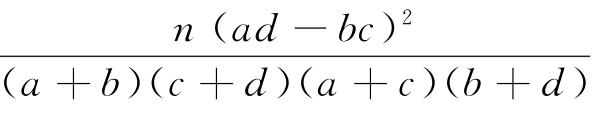，其中n=a+b+c+d.参考数据：

14.2016年备受瞩目的二十国集团领导人第十一次峰会于9月4-5日在杭州举办，杭州G20筹委会已经招募培训翻译联络员1000人、驾驶员2000人.为测试培训效果，采取分层抽样的方法从翻译联络员、驾驶员中共随机抽取60人，对其做G20峰会主题及相关服务职责进行测试，将其所得分数（分数都在60～100分之间）制成频率分布直方图如下图所示，若得分在90分及其以上（含90分）者，则称其为“G20通”.

（1）能否有90%的把握认为“G20通”与所从事工作（翻译联络员或驾驶员）有关？

（2）从参加测试的成绩在80分以上（含80分）的驾驶员中随机抽取4人，4人中“G20通”的人数为随机变量X，求X的分布列与数学期望.

附：K2=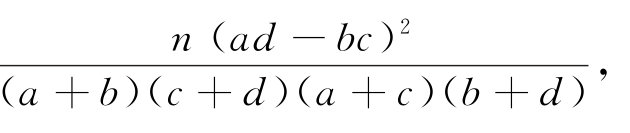其中n=a+b+c+d.

15.（2017福建宁德三模）随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查50人，并将调查情况进行整理后制成下表：

（1）世界联合国卫生组织规定：[15，45）岁为青年，[45，60）岁为中年，根据以上统计数据填写下面的2×2列联表：

（2）判断能否在犯错误的概率不超过0.05的前提下，认为赞成“车辆限行”与年龄有关；

附：K2=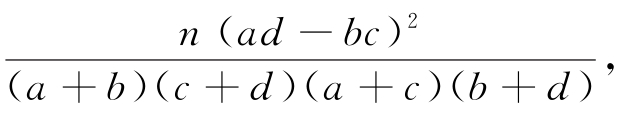其中n=a+b+c+d.

独立检验临界值表：

（3）若从年龄在[15，25），[25，35）岁的被调查者中各随机选取1人进行调查，设选中的两人中持不赞成“车辆限行”态度的人员为ξ，求随机变量ξ的分布列和数学期望E（ξ）.