考点：正弦定理和余弦定理（2016全国III，8）在△ABC中，B=，BC边上的高等于BC，则cos A=（）.AB.C.-D.-1.在△ABC中，a，b，c分别是内角A，B，C的对边，若bsinA=3csinB，a=3，cos B=，则b=（）.A.14B.6C.D.2.（2015天津南开一模）在△ABC中，角A，B，C的对边分别为a，b，c，且b2=a2+bc，A=......
2023-10-15
高考数学题：三角形求解题，正弦定理和余弦定理
【摘要】：考点：正弦定理和余弦定理的应用（2017全国I，17）△ABC的内角A，B，C的对边分别为a，b，c，已知△ABC的面积为（1）求sin B sin C；（2）若6cos B cos C=1，a=3，求△ABC的周长.1.（2016安徽安庆二模）如图，D是直角三角形ABC斜边BC上一点，AC=DC.（1）若∠DAC=30°，求角B的大小；（2）若BD=2DC，且AD=2，求DC的长.2.已知△AB
考点：正弦定理和余弦定理的应用
（2017全国I，17）△ABC的内角A，B，C的对边分别为a，b，c，已知△ABC的面积为
（1）求sin B sin C；
（2）若6cos B cos C=1，a=3，求△ABC的周长.
1.（2016安徽安庆二模）如图，D是直角三角形ABC斜边BC上一点，AC=
DC.
（1）若∠DAC=30°，求角B的大小；
（2）若BD=2DC，且AD=2
，求DC的长.
2.已知△ABC中的内角A，B，C的对边分别为a，b，c，
sin 2A+2cos2A=2，a=
.
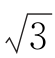（1）若cos B=
，求b；
（2）若2sin B=sin C，求△ABC的面积.
3.已知△ABC的外接圆半径为1，角A，B，C的对边分别为a，b，c，且2a cos A=c cos B+bcos C.
（1）求A；
（2）若b2+c2=7，求△ABC的面积.
4.（2015湖北鄂州三模）如图所示，在四边形ABCD中，∠D=2∠B，且AD=1，CD=3，cos B=
.
（1）求△ACD的面积；
（2）若BC=2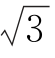
，求AB的长.
5.（2017广东潮州二模）在锐角三角形ABC中内角A，B，C所对的边分别为a，b，c，且
=
sin C.
（1）求∠C；
（2）若
=2，求△ABC面积S的最大值.
6.已知函数f（x）=A（sin
cos φ+cos
sin φ）（A＞0，0＜φ＜
）的最大值是2，且f（0）=1.
（1）求φ的值；
（2）已知锐角△ABC的内角A，B，C的对边分别为a，b，c，若a=2，f（2A）=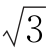
，2bsin C=
c.求△ABC的面积.
7.在△ABC中内角A，B，C所对应的边分别为a，b，c，a-b=bcos C.
（1）求证：sin C=tan B；
（2）若a=1，C为锐角，求c的取值范围.
8.如图，在平面四边形ABCD中，AD=1，CD=2，AC=7.
（1）求cos∠CAD的值；
（2）若cos∠BAD=-
，sin∠CBA=
，求BC的长.(www.chuimin.cn)
9.已知在△ABC中，内角A，B，C的对边分别为a，b，c，且
=
（1）求
的值；
（2）若cos B=
，b=2，求△ABC的面积S.
10.在△ABC中，D是BC中点，已知∠BAD+∠C=90°.
（1）判断△ABC的形状；
（2）若△ADC的三边长是连续三个正整数，求∠BAC的余弦值.
11.如图，在平面四边形ABCD中，已知∠A=
，∠B=
，AB=6，在AB边上取点E，使得BE=1，连接EC，ED.若∠CED=
，EC=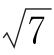
.
（1）求sin∠BCE的值；
（2）求CD的长.
12.（2017江西九江三模）在△ABC中，内角A，B，C所对的边分别为a，b，c，且满足sin2B+sin2C=sin2A+2sin Bsin Csin（B+C）.
（1）求角A的大小；
（2）若a=2，求△ABC面积的最大值.
13.（2017福建三明二模）在△ABC中，内角A，B，C所对的边分别为a，b，c，且B=60°，c=4.
（1）若b=6，求角C的正弦值及△ABC的面积；
（2）若D，E在线段BC上，且BD=DE=EC，AE=2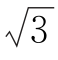
BD，求AD的长.
14.如图，在平面四边形ABCD中，AB=2，AD=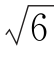
+
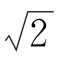，BC=2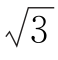
，∠ABC=120°，∠DAB=75°.
（1）设△ABC，△ABD的面积分别为S1，S2，求证：S1＜S2；
（2）求BD和DC的长.
15.如图，在△ABC中，AB=2，cos B=
，点D在线段BC上.
（1）若∠ADC=
π，求AD的长；
（2）若BD=2DC，△ADC的面积为
，求
的值.
16.在△ABC中，内角A，B，C的对边分别为a，b，c.已知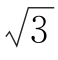
a=b（sin C+
cos C）.
（1）求角B的大小；
（2）若b=2，求a+c的取值范围.
17.已知△ABC的三个内角A，B，C所对的边分别为a，b，c，且满足
c cos（2016π-B）-sin（2017π+C）=0.
（1）求角B的大小；
（2）若动点D在△ABC的外接圆上，且点D，B不在AC的同一侧，AC=7，试求△ACD面积的最大值.
有关高考有套路 数学 全国卷的文章
- 详细阅读
-
高考数学：二项式定理应用与解题详细阅读
考点：二项式定理（2x+）5的展开式中，x3的系数是___________.1.在（2+x）6的展开式中，x5的系数是___________.2.若（x+） 10的展开式中x6的系数为30，则a=________.3.在7的展开式中，x2的系数为___________.4.设a=d x，则二项式（）6的展开式中常数项是___________.5.已知（x-1）6展开式中含x2项的系数为0，则正实数a=________.6.设（1-x）5=a0+a1x+a2x2+…......
2023-10-15
-
切线长定理的优化：三角形的切线长定理详细阅读
1．下列关于三角形的内心的说法中，正确的是（ ）．A．内心是三角形三条角平分线的交点B．内心是三角形三边中垂线的交点C．内心到三角形三个顶点的距离相等D．钝角三角形的内心在三角形外2．如图，⊙O为△ABC的内切圆，AC＝9，AB＝8，BC＝10，点D，E分别为BC，AC上的点，且DE为⊙O的切线，则△CDE的周长为（ ）．A．9 B．7 C．11 D．8（第2题）（第3题）3．如图，在△ABC中，......
2023-07-03
-
高考数学题空缺问题总和公式数列规律详细阅读
+b2n-1+b2n=__________.15.已知数列{an}的前n项和为Sn，若a1=1，a2n=n-an，a2n+1=an+1，则S100=____.16.已知数列{an}中，a1=-1，an+1=2an+3n-1，则其前n项和Sn=__________.17.设数列{an}满足a1=2，a2=6，且an+2-2an+1+an=2，用[x]表示不超过x的最大整数，如[0.6]=0，[1.2]=1，则[+…+]的值用m表示为__________.18.已知数列{an}中，a1=a，an+1=3an+8n+6，若{an}为递增数列，则实数a的取值范围为___________.19.已知数列{an}中，a1=1，......
2023-10-15
-
高考数学题－平面向量及坐标运算详细阅读
续表考点1：向量的线性运算1.（2017全国I，13）已知向量a，b的夹角为60°，|a|=2，|b|=1，则|a+2b|=___________.考点2：平面向量的数量积2.（2014全国I，15）已知A，B，C为圆O上的三点，若=，则与的夹角为___________.1.已知点A（1，-1），B（3，0），C（2，1）.若平面区域D由所有满足（1≤λ≤2，0≤μ≤1）的点P组成，则D的面积为_......
2023-10-15
- 详细阅读
-
三角形内角之和定理：陈省身与数学之路详细阅读
陈省身认为最重要的定理是“三角形内角和定理”与“勾股定理”。我们熟知的“三角形内角和定理”仅在平面上成立,而一般曲面上的三角形其内角和就不是常数了。高斯于1827 年证明了曲面上的三角形内角和公式,后法国数学家博内推广了该公式。1944 年陈省身完成了高斯-博内公式的简单内蕴证明,攻克了“几何学中极其重要和困难的问题”,该论文被誉为数学史上划时代的杰作。......
2023-11-23
-
罗尔定理的证明和费马定理的基本性质详细阅读
从几何上可以看到：在对于两端高度相等的连续光滑曲线上，必存在一条水平的切线（如图3－1所示），这便是罗尔定理.为了罗尔定理证明的需要，下面先给出极值的定义和极值点的一条基本性质——费马定理.图3－1定义1设f（x）在点x0的某邻域内有定义，若x∈（x0，δ），恒有f（x）＜f（x0）（或f（x）＞f（x0）），则称f（x0）为f（x）的一个极大值（或极小值），函数的极大值与极小值统称为函数的极值......
2023-11-19
相关推荐