续表考点1：向量的线性运算1.（2017全国I，13）已知向量a，b的夹角为60°，|a|=2，|b|=1，则|a+2b|=___________.考点2：平面向量的数量积2.（2014全国I，15）已知A，B，C为圆O上的三点，若=，则与的夹角为___________.1.已知点A（1，-1），B（3，0），C（2，1）.若平面区域D由所有满足（1≤λ≤2，0≤μ≤1）的点P组成，则D的面积为_......
2023-10-15
高考数学题空缺问题总和公式数列规律
【摘要】：+b2n-1+b2n=__________.15.已知数列{an}的前n项和为Sn，若a1=1，a2n=n-an，a2n+1=an+1，则S100=____.16.已知数列{an}中，a1=-1，an+1=2an+3n-1，则其前n项和Sn=__________.17.设数列{an}满足a1=2，a2=6，且an+2-2an+1+an=2，用[x]表示不超过x的最大整数，如[0.6]=0，[1.2]=1，则[+…+]的值用m表示为__________.18.已知数列{an}中，a1=a，an+1=3an+8n+6，若{an}为递增数列，则实数a的取值范围为___________.19.已知数列{an}中，a1=1，
专题1：导数在函数中的应用
1.（2017全国I，16）如图，圆形纸片的圆心为O，半径为5cm，该纸片上的等边三角形ABC的中心为O.D，E，F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得点D，E，F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积（单位：cm3）的最大值为___________.
专题2：圆锥曲线
2.（2017全国II，16）已知F是抛物线C：y2=8x的焦点，M是C上一点，FM的延长线交y轴于点N.若M为FN的中点，则|FN|=__________.
专题3：空间直线与平面的平行与垂直
3.（2017全国III，16）a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：
①当直线AB与a成60°角时，AB与b成30°角；
②当直线AB与a成60°角时，AB与b成60°角；
③直线AB与a所成角的最小值为45°；
④直线AB与a所成角的最小值为60°.
其中正确的是__________.（填写所有正确结论的编号）
专题4：不等式的应用与线性规划
4.（2016全国I，16）某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时.生产一件产品A的利润为2100元，生产一件产品B的利润为900元.该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为___________元.
专题5：直线与圆
5.（2016全国III，16）已知直线l：mx+y+3m-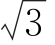
=0与圆x2+y2=12交于A，B两点，过A，B分别作l的垂线与x轴交于C，D两点，若|AB|=2
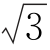，则|CD|=__________.
专题6：解三角形
6.（2015全国I，16）在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是___________.
专题7：数列
7.（2015全国II，16）设Sn是数列{an}的前n项和，且a1=-1，an+1=SnSn+1，则Sn=__________.
1.（2017河北保定二模）已知定义在（0，+∞）上的函数f（x）的导函数f′（x）是连续不断的，若方程f′（x）=0无解，且∀x∈（0，+∞），f（f（x）-log2015x）=2017，设a=f（20.5），b=f（log43），c=f（logπ3），则a，b，c的大小关系为__________.
2.若曲线C1：y=ax2（a＞0）与曲线C2：y=ex存在公切线，则a的取值范围为___________.
3.（2017河北邯郸二模）已知抛物线C：y2=2px（p＞0）的焦点为F，以抛物线C上的点M（x0，2 2）（x0＞
）为圆心的圆与线段MF相交于点A，且被直线x=
截得的弦长为
，若
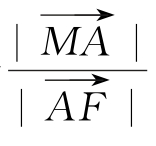=2，则
=__________.
4.（2017湖南郴州四模）在△ABC中a，b，c分别是角A，B，C的对边，△ABC的面积为S，（a2+b2）tan C=8S，且sin A cos B=2cos A sin B，则cos A=__________.
5.（2017江西上饶二模）如图，在长方体ABCD-A1B1C1D1中，AB=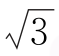
AD=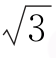
AA1=3，点P为线段A1C上的动点（包含线段端点），则下列结论正确的___________.(www.chuimin.cn)
①当
=3
时，D1P∕∕平面BDC1；
②当
=5
时，A1C⊥平面D1AP；
③∠APD1的最大值为90°；
④AP+PD1的最小值为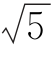
.
6.在△ABC中，∠A=
，O为平面内一点，且
，M为劣弧
上一动点，且
.则p+q的取值范围为__________.
7.（2017河南安阳三模）已知不等式组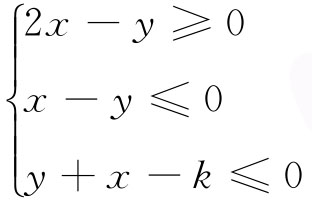
表示的平面区域的面积为
，则
的取值范围为___________.
8.（2017山西太原二模）已知点O是△ABC的内心，∠BAC=30°，BC=1，则△BOC面积的最大值为___________.
9.（2017河北保定二模）在△ABC中，A=
，BC=3，D是BC的一个三等分点，则AD的最大值是___________.
10.在等腰三角形ABC中，AB=AC，若AC边上的中线BD的长为6，则△ABC的面积的最大值是__________.
11.如图，在△ABC中，∠B=
，AC=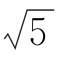
，D是AB边上一点，CD=2，△ACD的面积为2，∠ACD为锐角，则BC=__________.
12.（2017广东汕头二模）
如图，在△ABC中，B=
，点D在边AB上，BD=2，且DA=DC，AC=2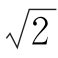
，则∠DCA=___________.
13.如图所示的“数阵”的特点是：每行每列都成等差数列，则数字37在图中出现的次数为__________.
14.数列{an}的前n项和为Sn，且a1=
，an+1-Sn=
，用[x]表示不超过x的最大整数，如[-0.1]=-1，[1.6]=1，设bn=[an]，则数列{bn}的前2n项和b1+b2+b3+b4+…+b2n-1+b2n=__________.
15.已知数列{an}的前n项和为Sn，若a1=1，a2n=n-an，a2n+1=an+1，则S100=____.
16.已知数列{an}中，a1=-1，an+1=2an+3n-1（n∈N*），则其前n项和Sn=__________.
17.（2017陕西咸阳三模）设数列{an}满足a1=2，a2=6，且an+2-2an+1+an=2，用[x]表示不超过x的最大整数，如[0.6]=0，[1.2]=1，则[
+…+
]的值用m表示为__________.
18.（2017河北石家庄一模）已知数列{an}中，a1=a，an+1=3an+8n+6，若{an}为递增数列，则实数a的取值范围为___________.
19.（2017河北保定一模）已知数列{an}中，a1=1，an-an-1=n（n≥2，n∈N*），设bn=
+…+
，若对任意的正整数n，当m∈[1，2]时，不等式m2-mt+
＞bn恒成立，则实数t的取值范围是___________.
20.已知函数f（x）=x2cos
，数列{an}中，an=f（n）+f（n+1）（n∈N*），则数列{an}的前100项之和S100=__________.
21.（2017江西九江三模）已知数列{an}的前n项和Sn，且满足a1=1，an·an+1=2Sn，设bn=
，若存在正整数p，q（p＜q），使得b1，bp，bq成等差数列，则p+q=__________.
22.（2017广东珠海二模）数列{an}满足a1=
，an+1-1=an（an-1），n∈N*且Sn=
+
+…+
，则Sn的整数部分的所有可能值构成的集合是___________.
有关高考有套路 数学 全国卷的文章
- 详细阅读
- 详细阅读
-
高考数学卷考察数列的激活码解答详细阅读
专题1：数列1.几位大学生响应国家的创业号召，开发了一款应用软件.为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…......
2023-10-15
-
高考自主权：高等教育规律与社会实践详细阅读
2003年,教育部谨慎推出高校自主招生改革试点。但笔者认为,自主招生的改革力度还不够大,今后应强化遵循高等教育发展规律意识,在以下方面大力践行高校自主招生权。二是强化高校招生多样化意识,为“奇才怪才”等特殊人才开辟绿色通道。多样化是欧美高等教育发达国家招生与办学深为倚重的重要理念,也被实践证明是符合高等教育办学规律的科学理念。......
2023-11-26
-
高考:教育与社会的平衡问题详细阅读
另一方面,“分数至上”在实践中成为我国高等学校招生录取的最高准则。平等主义盛行,录取环节开创性的尝试被视为腐败滋生的根源,进而导致高等学校招生环节中考试的地位凸显、招生的地位式微,最终的结果是以“分数至上”为实践逻辑,全面发展目标被悬置。......
2023-11-26
-
高考自主改革的影响与问题详细阅读
基于上述变化,自主招生改革的教育与社会影响逐渐显现与扩大。由于录取制度刚性,标准单一,高校基本上没有招生自主权,中学教学也因此陷入“片追”与应试教育的泥潭不能自拔。扩大高校招生自主权,推进素质教育,探索一种以统一考试为主、多元考试评价、多样选拔录取相结合的高校招生制度,成为教育改革的迫切需要。但毋庸讳言,改革也出现不少问题,在公平、诚信、自主考试的科学性、成本与效益、应试倾向等方面都受到不少质疑。......
2023-11-26
-
高考数学题解析：三角恒等变换、导函数与函数的详细阅读
其中正确的是__________..10.已知函数f=sin x+cos x，f′是f的导函数.若f=2f′，则=__________.......
2023-10-15
-
高考手记：解决偏科问题，确保录取详细阅读
我市不少考生，综合分达到了省划定的第一批或第二批录取最低控制线，而选科的分数却达不到第一、二批的资格线，有的甚至连第四批线都还差几分，所谓“跛脚”，这里，就暴露出了我们在教学中偏科问题的严重。考场如战场，稍有放松一科，成绩就势必拉下，“跛脚”分的现象就更加令人头痛，到时要登上龙门，更是难上加难了。......
2023-12-05
相关推荐