续表考点：三角函数（2017全国I，9）已知曲线C1：y=cos x，C2：y=sin（2x+），则下面结论正确的是（）.A.把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得曲线C2B.把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2C.把C1上各点的横坐标缩短到原来的，纵坐标不变，再把得到的曲线向右平移个单......
2023-10-15
高考数学题解析：三角恒等变换、导函数与函数的关系
【摘要】：其中正确的是__________..10.已知函数f=sin x+cos x，f′是f的导函数.若f=2f′，则=__________.
专题1：和与差的三角函数公式
1.（2013全国II，15）设θ为第二象限角，若tan（θ+
）=
，则sinθ+cosθ=_______.
专题2：简单的三角恒等变换
2.（2013全国I，15）设当x=θ时，函数f（x）=sin x-2cos x取得最大值，则cosθ=___________.
1.（2015辽宁葫芦岛一模）已知函数f（x）=cos x·sin（x+
）-
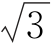cos2x+
，x∈R，则f（x）在闭区间[-
]上的最大值和最小值分别为___________.
2.已知tan（3π-α）=-
，tan（β-α）=-
，则tanβ=__________.
3.在锐角三角形ABC中，sinA=
，tan（AB）=-
，则tanC的值为___________.
4.已知tanα=
，且sin（2α+β）=2sinβ，则tan（α+β）=__________.(www.chuimin.cn)
5.设函数f（x）=1+sin2x，g（x）=2cos2x+m，若存在x0∈[0，
]，f（x0）≥g（x0），则实数m的取值范围是___________.
6.已知α，β∈（
，π），cos（α+β）=
，cos（β-
）=-
，则sin（α+
）=__________.
7.（2015广东广州二模）已知f（x）=sin（x+
），若cosα=
（0＜α＜
），则f（α+
）=__________.
8.（2015山东淄博二模）若x，y都是锐角，且sin x=
，tany=
，则x+y=________.
9.关于函数f（x）=sin2x+sin x+cos x，以下说法：①周期为2π；②最小值为-
；③在区间（0，
）上单调递增；④关于x=
对称。其中正确的是__________.（填上所有正确说法的序号）.
10.已知函数f（x）=sin x+cos x，f′（x）是f（x）的导函数.若f（x）=2f′（x），则
=__________.
有关高考有套路 数学 全国卷的文章
- 详细阅读
-
三角函数与双曲函数应用详细阅读
由复变函数的指数形式和三角形式可知,当x=0时,eiy =cos y+i sin y,e-iy =cos y-i sin y.将以上两式相加与相减,分别得到现在把实变量y推广到复变量z的情况,我们有如下定义：定义4 对任意的复数z,定义正弦函数与余弦函数分别为根此定义,我们不难验证复变数的正弦函数与余弦函数具有下列性质:(1) 由于ez是以2πi为周期的周期函数,所以sin z与cos z都是以2......
2023-10-30
-
复变函数与调和函数的关系详细阅读
前面我们证明了在区域D内的解析函数,其导数仍为D内的解析函数,下面我们用这个结论来研究解析函数与调和函数的关系.定义1 若φ(x,y)在平面区域D内有二阶连续偏导数,并且满足拉普拉斯(Laplace)方程则称φ=φ(x,y)在D内为调和函数.引入记号称为Laplace算子,则式(3.5.1)可简记为△φ=0.定理1 若函数f(z)=u(x,y)+iv(x,y)在区域D内解析,则u=u(x,y)和v......
2023-10-30
-
解析函数概念|复变函数及应用详细阅读
解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下：定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2023-10-30
-
入门至精通，EQ函数与EQUAL函数解析详细阅读
前面我们介绍了等值比较函数“=”，它只能用于数、符号原子和字符串，即原子的等值比较函数，它不能用于表。eq函数用于检查两个表达式＜expr1＞和＜expr2＞是否约束于同一对象，即它们不仅值相等，而且占用同一内存单元。因此，任选变元＜fuzz＞可以让用户指定表达式＜expr1＞和＜expr2＞间的最大差值，在此范围内，仍然认为＜expr1＞和＜expr2＞是相等的。所有同源值一定相等不同源时，INTREALSTR类型一定相等不同源时，ENAME类型，“=”不等，“eqequal”相等。......
2023-11-02
-
拉氏变换性质|复变函数及应用详细阅读
这一节将介绍拉氏变换的几个基本性质,它们在拉氏变换的实际应用中都是很有用的.为了叙述方便,假定在这些性质中,凡是要取拉氏变换的函数都满足拉氏变换存在定理中的条件,并且把这些函数的增长指数统一地设为c.在证明这些性质时,不再重复这些条件.1.线性性质设α,β为常数,且则有或2.相似性质设a ＞0,若L[f(t)]=F (p),则类似有以上两条性质的证明与傅氏变换相应的性质的证明是一样的.3.微分性质......
2023-10-30
-
矢端函数曲线的起伏与光矢量变换色谱理论解析详细阅读
经验告诉我们，热辐射光源，如太阳光、白炽灯等它们复频谱的矢端函数曲线虽有起伏，但比较平缓。甲光源与另一个等能光源两个矢端函数曲线包围的面积相等，即A=A0，示意图如图11-1所示。在这里，以等能光源矢径r0为基准，判断甲光源矢端函数曲线起伏变化的状态。全频域光源矢端函数曲线起伏变化总评价值为：Q值在100到0之间，100最好，0最差。......
2023-11-18
-
高考数学有套路全国卷中的函数及基本初等函数详细阅读
续表考点1：函数1.（2017全国I，5）函数f（x）在（-∞，+∞）上单调递减，且为奇函数.若f（1）=-1，则满足-1≤f（x-2）≤1的x的取值范围是（）.A.[-2，2]B.[-1，1]C.[0，4]D.[1，3]考点2：对数函数2.（2017全国I，11）设x，y，z为正数，且2x=3y=5z，则（）.A.2x＜3y＜5zB.5z＜2x＜3yC.3y＜5z＜2xD......
2023-10-15
相关推荐