}B.{0,2,4,6,8,…}C.{1,3,5,7,…......
2023-10-15
续表
考点1:函数
1.(2017全国I,5)函数f(x)在(-∞,+∞)上单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( ).
A.[-2,2] B.[-1,1]
C.[0,4] D.[1,3]
考点2:对数函数
2.(2017全国I,11)设x,y,z为正数,且2x=3y=5z,则( ).
A.2x<3y<5z B.5z<2x<3y
C.3y<5z<2x D.3y<2x<5z
考点3:幂函数
3.(2016全国III,6)已知a= ,b=
,b=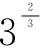 ,c=
,c=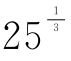 ,则( ).
,则( ).
A.b<a<c B.a<b<c
C.b<c<a D.c<a<b
1.设函数f(x)=min{x2-1,x+1,-x+1},其中min{x,y,z}表示x,y,z中的最小者.若f(a+2)>f(a),则实数a的取值范围为( ).
A.(-1,0)
B.[-2,0]
C.(-∞,-2)∪(-1,0)
D.[-2,+∞)
2.偶函数f(x)=loga|x+b|在(-∞,0)上单调递减,则f(a+1)与f(2-b)的大小关系是( ).
A.f(a+1)>f(2-b)
B.f(a+1)=f(2-b)
C.f(a+1)<f(2-b)
D.不能确定
3.已知偶函数f(x)在区间[0,+∞)上单调递增,则满足f(2x-1)<f()的x的取值范围是( ).
A.(![]() ) B.[
) B.[![]() )
)
C.(![]() ) D.[
) D.[![]() )
)
4.下列函数中,与函数y=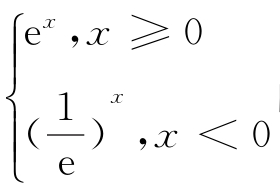 的奇偶性相同,且在(-∞,0)上单调性也相同的是( ).
的奇偶性相同,且在(-∞,0)上单调性也相同的是( ).
A.y=-![]() B.y=x2+2
B.y=x2+2
C.y=x3-3 D.y=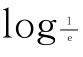 |x|
|x|
5.(2015浙江丽水一模)定义在实数集R上的奇函数f(x),对任意实数x都有f(![]() +x)=f(
+x)=f(![]() -x),且满足f(1)>-2,f(2)=m-
-x),且满足f(1)>-2,f(2)=m-![]() ,则实数m的取值范围是( ).
,则实数m的取值范围是( ).
A.-1<m<3(www.chuimin.cn)
B.0<m<3
C.0<m<3或m<-1
D.m>3或m<-1
6.已知x=log23-log2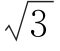 ,y=log0.5π,z=0.9-1.1,则( ).
,y=log0.5π,z=0.9-1.1,则( ).
A.x<y<z B.z<y<x
C.y<z<x D.y<x<z![]()
7.(2015陕西宝鸡一模)设a=log37,b=23.3,c=0.83.3,则( ).
A.b<a<c B.c<a<b
C.c<b<a D.a<c<b
8.已知实数x,y满足ax<ay(0<a<1),则下列关系式恒成立的是( ).
A![]()
B.ln(x2+1)>ln(y2+1)
C.sin x>siny
D.x3>y3
9.设f(x)=|lg(x-1)|,若0<a<b,且f(a)=f(b),则ab的取值范围是( ).
A.[1,2] B.(1,2)
C.(4,+∞) D.(2,+∞)
10.(2017青海西宁二模)现有四个函数:①y=x·sin x;②y=x·cos x;③y=x·|cos x|;④y=x·2x的图像(部分)如图:
则按照从左到右将图像对应的函数序号排列正确的一组是( ).
A.①④③② B.③④②①
C.④①②③ D.①④②③
11.(2015山东潍坊一模)已知函数y=f(x)的定义域为{x|x≠0},满足f(x)+f(-x)=0,当x>0时,f(x)=lgx-x+1,则函数y=f(x)的大致图像是( ).
A.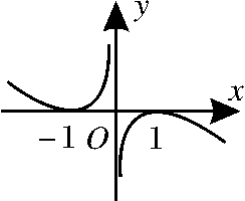 B.
B.
C.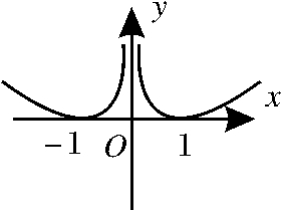 D.
D.
12.(2017河北石家庄一模)函数f(x)=ex-3x-1(e为自然对数的底数)的图像大致是( ).
A. B.
B.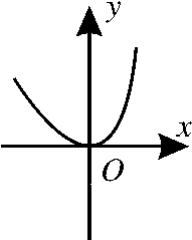
C. D.
D.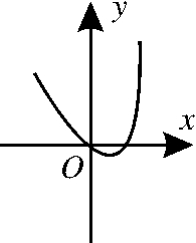
13.(2015安徽马鞍山二模)如图所示的图形是由一个半径为2的圆和两个半径为1的半圆组成,它们的圆心分别为O,O1,O2.动点P从点A出发沿着圆弧按A→O→B→C→A→D→B的路线运动(其中A,O1,O,O2,B五点共线),记点P运动的路程为x,设y=|O1P|2,y与x的函数关系为y=f(x),则y=f(x)的大致图像是( ).
A. B.
B.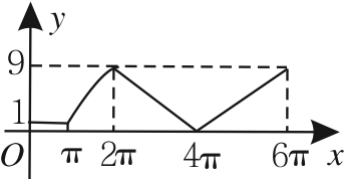
C.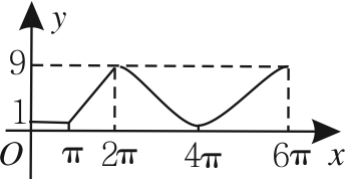 D.
D.
有关高考有套路 数学 全国卷的文章

A.{2}B.{4,6}C.{1,3,5}D.{2,4,6}20.设全集U=R,集合A={x|x2-2x-3<0},B={x|x-1≥0},则图中阴影部分所表示的集合为().A.{x|x≤-1或x≥3}B.{x|x<1或x≥3}C.{x|x≤1}D.{x|x≤-1}21.已知A,B均为集合U={1,3,5,7,9}的子集,且A∩B={3},UB∩A={9},则A等于().A.{1,3}B.{3,7,9}C.{3,5,9}D.{3,9}......
2023-10-15

续表考点1:坐标系1.(2017全国II,22)在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM||OP|=16,求点P的轨迹C2的直角坐标方程;(2)设点A的极坐标为(2,),点B在曲线C2上,求△OAB面积的最大值.考点2:参数方程2.(2017全国I,22)在直角坐标系xOy......
2023-10-15

一、基本初等函数我们常用的基本初等函数有6种,分别是常数函数、指数函数、对数函数、幂函数、三角函数及反三角函数.(一)常数函数y=c(c为常数).(二)幂函数1.函数y=xα称为幂函数,其中x是自变量,α是常数.2.幂函数的性质及图像的变化规律①所有的幂函数在(0,+∞)都有定义,并且图像都过点(1,1).图1.9②α>0时,幂函数的图像通过原点和点(1,1),并且在区间[0,+∞)上是增函数.③......
2023-11-20

续表考点:导数在研究函数中的应用(2017全国I,21)已知函数f(x)=ae2x+(a-2)ex-x.(1)讨论f(x)的单调性;(2)若f(x)有两个零点,求a的取值范围.1.(2017山东莱芜二模)已知函数f(x)=ex[x2+(a+1)x+2a-1].(1)当a=-1时,求函数f(x)的单调区间;(2)若关于x的不等式f(x)≤ea在[a,+∞)上有解,求实数a的取值范围;(3)若曲线y=......
2023-10-15

1)反函数设函数y=f(x)的定义域为D,值域为f(D),在函数y=f(x)中,x为自变量,y为因变量,x可以独立取值,而y却按确定的法则随x而定,即函数y=f(x)反映的是y怎样随x而定的法则;反过来,对于y∈f(D),若D内总有确定的x与之对应,使得f(x)=y成立,这样得到一个以y为自变量,x为因变量的函数,称该函数为y=f(x)的反函数,记作x=f-1(y),其定义域为f(D),值域为D.......
2023-11-19

考点1:命题及其关系1.(2017全国I,3)设有下面四个命题:p1:若复数z满足∈R,则z∈R;p2:若复数z满足z2∈R,则z∈R;p3:若复数z1,z2满足z1z2∈R,则z1=;p4:若复数z∈R,则∈R.其中真命题为().A.p1,p3B.p1,p4C.p2,p3D.p2,p4考点2:全称量词与存在量词2.(2014全国I,9)不等式组的解集记为D,有下列四个命题:p1:(x......
2023-10-15

其中正确的是__________..10.已知函数f=sin x+cos x,f′是f的导函数.若f=2f′,则=__________.......
2023-10-15
相关推荐