【摘要】:+的结果,下面程序框图中的横线上可以填().A.n<2016B.n≤2016C.n>2016D.n≥201611.某市高三数学抽样考试中,对90分以上的成绩进行统计,其频率分布图如图②所示,已知130~140分数段的人数为90,90~100分数段的人数为a,则图①所示程序框图的运算结果为(注:n!
考点:算法的含义、程序框图
(2017全国I,8)如图,程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在◇和□两个空白框中,可以分别填入( ).
A.A>1000和n=n+1
B.A>1000和n=n+2
C.A≤1000和n=n+1
D.A≤1000和n=n+2
1.某流程图如图所示,现输入如下四个函数,则可以输出的函数是( ).
A.f(x)=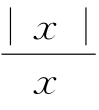
Bf.(x)=lg(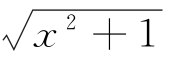 -x)
-x)
C.f(x)=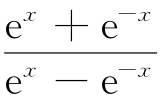
D.f(x)=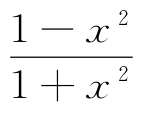
2.某调查机构对某地区小学学生课业负担情况进行了调查,设平均每人每天做作业的时间为x min,有1000名小学生参加了此项调查,调查所得数据用程序框图处理,若输出的结果是320,则平均每天做作业的时间在0~60 min(包括60 min)内的学生的频率是( ).
A.680 B.320 C.0.68 D.0.32
3.(2014山东枣庄一模)执行两次如图所示的程序框图,若第一次输入的a的值为-1.2,第二次输入的a的值为1.2,则第一次、第二次输出的a的值分别为( ).
A.0.2,0.2 B.0.2,0.8
C.0.8,0.2 D.0.8,0.8
4.若执行如图所示的程序框图,当输入的x的值为4时,输出的y的值为2,则空白判断框中的条件可能为( ).
A.x>3 B.x>4 C.x≤4 D.x≤5
5.如图所示的程序运行结果为( ).
A.3 B.4 C.5 D.6
6.(2014湖南郴州三模)阅读下面的程序,若输入的x的值为987654,则输出的a的值为( ).
A.5 B.6 C.7 D.8
7.在如图所示的程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),能输出“恭喜中奖!”的概率为( ).(www.chuimin.cn)
A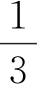 B.
B. C.
C.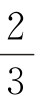 D.
D.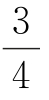
8.(2015山西太原一模)执行如图所示的程序框图,则输出a=( ).
A.20 B.14 C.10 D.7
9.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入的x的值为2,则输出的v的值为( ).
A.210-1 B.210
C.310-1 D.310
10.(2016安徽铜陵一模)要计算1+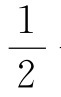 +
+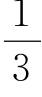 +…+
+…+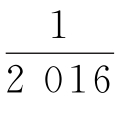 的结果,下面程序框图中的横线上可以填( ).
的结果,下面程序框图中的横线上可以填( ).
A.n<2016 B.n≤2016
C.n>2016 D.n≥2016
11.(2015四川内江五模)某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图②所示,已知130~140分数段的人数为90,90~100分数段的人数为a,则图①所示程序框图的运算结果为(注:n!=1×2×3×···×n,如5!=1×2×3×4×5)( ).
A.800! B.810! C.811! D.812!
12.某程序框图如图所示,该程序运行后输出的S的值是( ).
A.1007 B.2015 C.2016 D.3024
13.(2015湖南郴州二模)执行如图所示的程序框图,则输出的结果是( ).
A.-1007 B.1007
C.-2014 D.2014
14.已知实数x∈{1,2,3,4,5,6,7,8,9},执行如图所示的程序框图,则输出的x不小于121的概率为( ).
A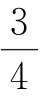 B.
B.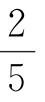 C.
C. D.
D.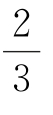
15.(2016山东济南一模)公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( ).
(参考数据: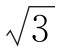 ≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
A.12 B.24 C.36 D.48

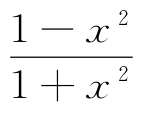
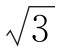 ≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)





相关推荐