在现实世界中,存在着各种各样的物体,它们都占据着一定的空间.如果只考虑这些物体的大小和形状,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.观察与思考仔细观察下面的图片,你能说出它们都是什么建筑吗?棱锥的结构特征观察与思考观察下面图片,说说图片中的几何体具有什么样的共同特征呢?......
2023-11-22
考点:空间几何体
(2017全国I,7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( ).
A.10 B.12
C.14 D.16
1.如图,已知球O是棱长为1的正方体ABCDA1B1C1D1的内切球,则平面ACD1截球O的截面面积为( ).
A![]() B.
B.![]()
C.![]() D.
D.![]()
2.(2015北京房山一模)一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图示,则该几何体的体积为( ).
A.7 B.![]() C.
C.![]() D.
D.![]()
3.如图,点P在正方体ABCD-A1B1C1D1的表面上运动,且P到直线BC与直线C1D1的距离相等,如果将正方体在平面内展开,那么动点P的轨迹在展开图中的形状是( ).
A.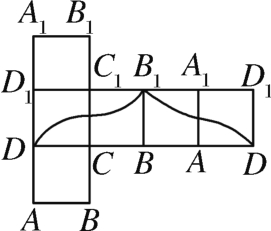 B.
B.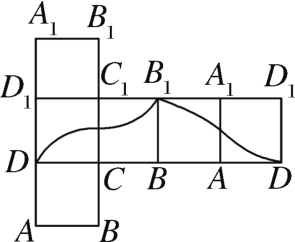
C.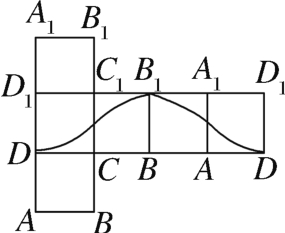 D.
D.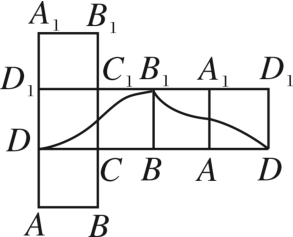
4.某几何体的三视图如图所示,则该几何体的体积为( ).
A.12 B.24 C.30 D.48
5.某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( ).
A.4+![]() B.6
B.6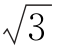 C.4+
C.4+![]() D.6
D.6
6.已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的四个侧面中的最大面积是( ).
A.6 B.8 C.2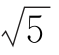 D.3
D.3
7.某几何体的正视图与侧视图如图所示,若该几何体的体积为![]() ,则该几何体的俯视图可以是( ).
,则该几何体的俯视图可以是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则几何体的体积为( ).
A![]() B.
B.![]() C.1 D.
C.1 D.![]() (www.chuimin.cn)
(www.chuimin.cn)
9.某几何体的三视图如图所示,其中正视图是半径为1的半圆,则该几何体的表面积是( ).
A![]() +2 B.
+2 B.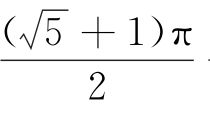 +2
+2
C.![]() +3 D.
+3 D.![]() +2
+2
10.已知某几何体的三视图如图所示,则该几何体的体积是( ).
A.28+6 B.40
B.40
C.![]() D.30+6
D.30+6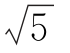
11.(2015北京昌平二模)一个几何体的三视图如图所示,则这个几何体的体积为( ).
A![]() +
+![]() B.
B.![]() +
+![]()
C.![]() +
+![]() D.4
D.4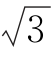 +
+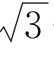 π
π
12.如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( ).
A.16 B.8 C.32 D.16
C.32 D.16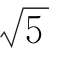
13.(2015黑龙江齐齐哈尔二模)已知一个底面为正六边形,侧棱长都相等的六棱锥的正视图与俯视图如图所示,若该几何体的底面边长为2,侧棱长为 ,则该几何体的侧视图可能是( ).
,则该几何体的侧视图可能是( ).
A.![]() B.
B.![]()
C.![]() D.
D.
14.(2014北京西城二模)某四棱锥的三视图如图所示,记A为此棱锥所有棱的长度的集合,则( ).
A.2∈A,且4∈A
B.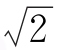 ∈A,且4∈A
∈A,且4∈A
C.2∈A,且2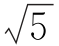 ∈A
∈A
D. ∈A,且
∈A,且 ∈A
∈A
15.(2015浙江温州二模)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( ).
A.(18π-20)cm3 B.(24π-20)cm3
C.(18π-28)cm3 D.(24π-28)cm3
有关高考有套路 数学 全国卷的文章

在现实世界中,存在着各种各样的物体,它们都占据着一定的空间.如果只考虑这些物体的大小和形状,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.观察与思考仔细观察下面的图片,你能说出它们都是什么建筑吗?棱锥的结构特征观察与思考观察下面图片,说说图片中的几何体具有什么样的共同特征呢?......
2023-11-22

用来表示空间几何体的平面图形,叫做空间几何体的直观图.空间几何体的直观图要有立体感,往往需要改变其真实的形状.例如,正方体的各个面都是正方形,但在直观图中,有些面画成了平行四边形.在立体几何中,空间几何体的直观图通常是在平行投影下画出的空间图形.依据平行投影的性质画直观图的方法,国家已经规定了统一的标准.一种较为简单的画图标准是斜二测画法.(1)平面图形直观图的画法例1用斜二测画法画水平放置的正......
2023-11-22

考点1:复数的概念1.(2016全国I,2)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=().A.1B.C.D.2考点2:复数的四则运算2.(2017全国II,1)=().A.1+2iB.1-2iC.2+iD.2-i1.(2016陕西渭南一模)复数z=1-i,则z-对应的点所在的象限为().A.第一象限B.第二象限C.第三象限D.第四象限2.......
2023-10-15

续表考点1:随机抽样1.(2013全国I,3)为了解某地区中小学生的视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大.在下面的抽样方法中,最合理的抽样方法是().A.简单的随机抽样B.按性别分层抽样C.按学段分层抽样D.系统抽样考点2:用样本估计总体2.(2017全国III,3)某城市为了解游客......
2023-10-15

A.{2}B.{4,6}C.{1,3,5}D.{2,4,6}20.设全集U=R,集合A={x|x2-2x-3<0},B={x|x-1≥0},则图中阴影部分所表示的集合为().A.{x|x≤-1或x≥3}B.{x|x<1或x≥3}C.{x|x≤1}D.{x|x≤-1}21.已知A,B均为集合U={1,3,5,7,9}的子集,且A∩B={3},UB∩A={9},则A等于().A.{1,3}B.{3,7,9}C.{3,5,9}D.{3,9}......
2023-10-15

教学目标1.通过实践活动探索测量一些无法直接计算的物体体积的方法,体会测量物体体积方法的多样性,提高综合应用数学知识和方法解决实际问题的能力。解决这个问题需要测量出皇冠的体积,可是皇冠是一个不规则的物体,阿基米德一直解决不了这个难题。A.用量筒测量,上升的水的体积就是铁螺丝的体积。】2.探究活动二:根据物体的密度和质量求体积。......
2023-08-11

考点:二项式定理(2x+)5的展开式中,x3的系数是___________.1.在(2+x)6的展开式中,x5的系数是___________.2.若(x+) 10的展开式中x6的系数为30,则a=________.3.在7的展开式中,x2的系数为___________.4.设a=d x,则二项式()6的展开式中常数项是___________.5.已知(x-1)6展开式中含x2项的系数为0,则正实数a=________.6.设(1-x)5=a0+a1x+a2x2+…......
2023-10-15
相关推荐