组合学源自对游戏的研究,但也应用于其他许多领域,比如密码学。这种现象被我们称作组合爆炸。这些组合学技巧通常在与自身相关的领域中有着非常实际的作用,而在一些看上去联系不大的领域里,比如拓扑,它们也有一定的作用。参考阅读//No. 14 自然数,第32页No. 92 阶乘,第188页No. 94 图形,第192页3.一分钟记忆组合学研究的是计数,特别是计算组合或者排列结果的数量。即便是对数量很少的事物进行排列组合,往往也会有很多种可能。......
2023-11-22
考点:排列与组合
(2017全国II,6)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( ).
A.12种 B.18种 C.24种 D.36种
1.(2015湖南怀化三模)北京某小学组织6个年级的学生外出参观包括甲博物馆在内的6个博物馆,每个年级任选一个博物馆参观,则有且只有两个年级选择甲博物馆的方案有( ).
A.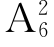 ×
× 种 B.
种 B. ×54种
×54种
C.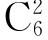 ×
×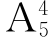 种 D.
种 D.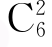 ×54种
×54种
2.甲、乙、丙、丁、戊五名应届师范毕业生分配到A,B,C三所学校任教,其中A学校和B学校均要2人,C学校要1人,且甲、乙两人不能到同一所学校任教,则不同的分配方案的种数为( ).
A.30 B.48 C.24 D.36
3.在某市举行“市民运动会”期间,组委会将甲、乙、丙、丁四位志愿者全部分配到A,B,C三个场馆执勤.若每个场馆至少分配一人,则不同分配方案的种数是( ).
A.96 B.72 C.36 D.24
4.有一个7人学习合作小组,从中选取4人发言,要求其中组长和副组长至少有一人参加,若组长和副组长同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序有( ).(www.chuimin.cn)
A.720种 B.600种 C.360种 D.300种
5.现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求取出的这些卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为( ).
A.232 B.252 C.472 D.484
6.从0,1,3,4,5,6六个数字中,选出一个偶数和两个奇数,组成一个没有重复数字的三位奇数,这样的三位数共有( )个.
A.24 B.30 C.36 D.48
7.(2017陕西渭南二模)在某商业促销的最后一场活动中,甲、乙、丙、丁、戊、己6名成员随机抽取4个礼品,每人最多抽一个礼品,且礼品中有两个完全相同的笔记本电脑,两个完全相同的山地车,则甲、乙两人都抽到礼品的情况有( )种.
A.36 B.24 C.18 D.9
8.两个三口之家,共4个大人,2个小孩,约定星期日乘“奥迪”“捷达”两辆轿车结伴郊游,每辆车最多只能乘坐4人,其中两个小孩不能独坐一辆车,则不同的乘车方法种数是( ).
A.40 B.48 C.60 D.68
有关高考有套路 数学 全国卷的文章

组合学源自对游戏的研究,但也应用于其他许多领域,比如密码学。这种现象被我们称作组合爆炸。这些组合学技巧通常在与自身相关的领域中有着非常实际的作用,而在一些看上去联系不大的领域里,比如拓扑,它们也有一定的作用。参考阅读//No. 14 自然数,第32页No. 92 阶乘,第188页No. 94 图形,第192页3.一分钟记忆组合学研究的是计数,特别是计算组合或者排列结果的数量。即便是对数量很少的事物进行排列组合,往往也会有很多种可能。......
2023-11-22

cr (9.1)进行一次a,b之间的对换,得到排列a1a2…cr. (9.2)我们证明排列(9.2)与排列(9.1)的奇偶性不同.首先在排列(9.1)中将数码a依次与其右边的数码进行相邻对换,进行s次相邻对换后得到排列a1a2…......
2023-11-22

组合式凹模是由两个或两个以上的零件组合而成的。因此,这种凹模主要用于形状复杂的塑件的成型。组合式凹模的组合形式很多,常见的有以下几种。......
2023-06-30

由于笔记本式计算机的普及和USB接口的应用,与单片机通信时大多采用USB接口进行。容值比较大的电容,主要是起到缓冲和稳定电路的作用。在图3-6中的另一种电容C10,它容值较小,是0.1 F,也就是100 nF,是用来滤除高频信号干扰的,如ESD,EFT等。同学们可以仔细观察自己所用的开发板和电路原理图,在电路中需要较大电流供给的器件附近,都会加一个大电容,如1602液晶、靠近单片机的VCC、1602液晶背光的VCC等,起到稳定电压的作用。......
2023-11-17

在工作方式0下进行计数时,计数值的范围是1~8192。使用定时功能时定时时间的计算公式为或其时间单位与晶振周期或机器周期的时间单位相同,为μs。方式0为13位计数结构。定时器/计数器0不用,所以保持其原来的控制位不变。程序设计定时器方式0例程说明......
2023-11-17

利用这一特性,可制造出各种半导体器件。图1-3 半导体的导电方式纯净半导体中,自由电子和空穴总是成对出现,称为电子-空穴对。在一定温度下,纯净半导体产生的电子-空穴对很少,所以导电能力很差。当环境温度升高时,其电子-空穴对的数目显著增加,导电能力明显提高,这就是半导体的导电性随温度而变化的原因。因为这种半导体的主要是电子导电,故称之为电子半导体或N型半导体。......
2023-06-22

逆向创新原理是从反面、从构成要素中对立的另一面分析,将通常思考问题的思路反转过来,有意识地按相反的视角去观察事物,寻找解决问题完全颠倒的新途径、新方法。逆向创新法也称反向探求法。当今世界上大量的新技术、新成果都是人们利用逆向创新原理不断探索创造出来的,是用传统思想方法所无法想象的。我国宋代司马光砸缸救小孩的故事,就是逆向思维方法,他不是将小孩拉出来而是用砸破水缸让水流走的办法,将小孩救出。......
2023-06-26
相关推荐