首页理论教育直线与圆，圆心到直线的距离，圆与直线围成的面积

直线与圆，圆心到直线的距离，圆与直线围成的面积

2025-09-30 理论教育版权反馈

【摘要】：续表考点：圆的方程（2016卷II，4）圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1，则a=（）.A.-B.-C.D.21.已知圆C：（x-1）2+（y-2）2=2与y轴在第二象限所围区域的面积为S，直线y=2x+b分圆C的内部为两部分，其中一部分的面积也为S，则b=（）.A.-B.±C.-D.±2.（2016河南洛阳四模）距某码头400km

续表

考点：圆的方程

（2016卷II，4）圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1，则a=（　　）.

A.-　　B.-　　C.　　D.2

1.已知圆C：（x-1）2+（y-2）2=2与y轴在第二象限所围区域的面积为S，直线y=2x+b分圆C的内部为两部分，其中一部分的面积也为S，则b=（　　）.

A.-　　B.±

C.-　　D.±

2.（2016河南洛阳四模）距某码头400km的正东方向有一个台风中心，正以20km/h的速度向西北方向移动，据经验，台风中心距码头300km时，将对码头产生影响，则这个台风对码头产生影响的时间为（　　）.

A.8h　　B.9h

C.10h　　D.12h

3.过点（3，1）作圆（x-1）2+y2=1的两条切线，切点分别为A，B，则直线AB的方程为（　　）.

A.2x+y-3=0　　B.2x-y-3=0

C.4x-y-3=0　　D.4x+y-3=0(https://www.chuimin.cn)

4.（2015浙江绍兴嵊州二模）已知圆（x+1）2+y2=4的圆心为C，点P是直线l：mx-y-5m+4=0上的点，若该圆上存在点Q使得∠CPQ=30°，则实数m的取值范围为（　　）.

A.[-1，1]　　B.[-2，2]

C.[]　　D.[0，]

5.（2017广东深圳一模）直线l：kx+y+4=0（k∈R）是圆C：x2+y2+4x-4y+6=0的一条对称轴，过点A（0，k）作斜率为1的直线m，则直线m被圆C所截得的弦长为（　　）.

A　　B.　　C.　　D.2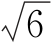

6.已知直线l：y=x+1平分圆C：（x-1）2+（y-b）2=4，则直线x=3同圆C的位置关系是（　　）.

A.相交　　B.相切

C.相离　　D.不能确定

7.若圆（x-3）2+（y+5）2=r2上有且只有三个点到直线4x-3y=2的距离等于1，则半径r等于（　　）.

A.3　　B.4　　C.5　　D.6

8.（2016内蒙古包头一模）已知圆心为C的圆经过点A（1，1）和B（2，-2），且圆心C在直线l：x-y+1=0上，则点C与坐标原点的距离为（　　）.

A.　　B.5　　C.13　　D.25