续表考点1：概率（2017全国I，19）为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm）.根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N（μ，σ2）.（1）假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在（μ-3σ，μ+3σ）之外的零件数，求P（X≥1）及X的数学期望；（2）一天内抽检零件中，如果出......
2023-10-15
高考数学：概率与统计初步
【摘要】：续表考点1：随机抽样1.（2013全国I，3）为了解某地区中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大.在下面的抽样方法中，最合理的抽样方法是（）.A.简单的随机抽样B.按性别分层抽样C.按学段分层抽样D.系统抽样考点2：用样本估计总体2.（2017全国III，3）某城市为了解游客
续表
考点1：随机抽样
1.（2013全国I，3）为了解某地区中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大.在下面的抽样方法中，最合理的抽样方法是（ ）.
A.简单的随机抽样
B.按性别分层抽样
C.按学段分层抽样
D.系统抽样
考点2：用样本估计总体
2.（2017全国III，3）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图.
根据该折线图，下列结论错误的是（ ）.
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7，8月
D.各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳
考点3：古典概型
3.（2014全国I，5）4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率为（ ）.
A
B.
C.
D.
考点4：随机数与几何概型
4.（2017全国I，2）如图，正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是（ ）.
A
B.
C.
D.
1.连续抛掷两次骰子得到的点数分别为m和n，记向量a=（m，n），向量b=（1，-2），则a⊥b的概率是（ ）.
A
B.
C.
D.
2.将1，2，3，4四个数字随机填入下面的2×2方格中，每个方格中恰填一数字，数字可重复使用.试问事件“a方格的数字大于b方格的数字，且c方格的数字大于d方格的数字”的概率为（ ）.
A
B.
C.
D.
3.（2017辽宁锦州一模）三国时期吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明，下面是赵爽的弦图及注文。弦图是一个以勾股形之弦为边的正方形，其面积称为弦实，图中包含四个全等的勾股形及一个小正方形，分别涂成红（朱）色及黄色，其面积称为朱实，黄实，利用2×勾×股+（股-勾）2=4×朱实+黄实=弦实，化简，得勾2+股2=弦2，设勾股中勾股比为1∶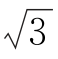
，若向弦图内随机抛掷1000颗图钉（大小忽略不计），则落在黄色图形内的图钉数大约为（ ）.
A.866 B.500 C.300 D.134
4.（2013北京东城一模）某游戏规则如下：随机地往半径为1的圆内投掷飞镖，若飞镖到圆心的距离大于
，则成绩为及格；若飞镖到圆心的距离小于
，则成绩为优秀；若飞镖到圆心的距离大于
且小于
，则成绩为良好，那么在所有投掷到圆内的飞镖中得到成绩为良好的概率为（ ）.
A
B.
C.
D.
5.如图，将半径为2的圆分成相等的四弧，再将四弧围成星形放在半径为2的圆内，现在往该圆内任投一点，此点落在星形内的概率为（ ）.
A
B.
(www.chuimin.cn)
C.
D.
-1
6.（2016广东深圳二模）2位男生和3位女生共5位同学站成一排，则3位女生中有且只有两位女生相邻的概率是（ ）.
A
B.
C.
D.
7.（2016广东深圳一模）4名同学参加3项不同的课外活动，若每名同学可自由选择参加其中的一项，则每项活动至少有一名同学参加的概率为（ ）.
A
B.
C.
D.
8.袋中装有完全相同的5个小球，其中有红色小球3个，黄色小球2个，如果不放回地依次摸出2个小球，则在第一次摸出红球的条件下，第二次摸出红球的概率是（ ）.
A
B.
C.
D.
9.两枚均匀的骰子一起投掷，记事件A={至少有一枚骰子6点向上}，B={两枚骰子都是6点向上}，则P（B|A）=（ ）.
A
B.
C.
D.
10.（2016江西萍乡二模）老师提出一个关于引力波的问题需要甲、乙两位同学回答，已知甲、乙两位同学能回答该问题的概率为0.4和0.5.在这个问题已被解答的条件下，甲、乙两位同学都能正确回答该问题的概率为（ ）.
A
B.
C.
D.
11.2016年鞍山地区空气质量的记录表明，一天的空气质量为优良的概率为0.8，连续两天为优良的概率为0.6.若今天的空气质量为优良，则明天空气质量为优良的概率是（ ）.
A.0.48 B.0.6 C.0.75 D.0.8
12.为了了解我校今年新入学的高一（1）班学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知高一（1）班学生人数为48人.图中从左到右的前3个小组的频率之比为1∶2∶3，则第2小组的频数为（ ）.
A.16 B.14 C.12 D.11
13.为了有效管理学生迟到问题，某校专对各班迟到现象制定了相应的等级标准，其中D级标准为“连续10天，每天迟到不超过7人”.根据过去10天1、2、3、4班的迟到数据，一定符合D级标准的是（ ）.
A.1班：总体平均值为3，中位数为4
B.2班：总体平均值为1，总体方差大于0
C.3班：中位数为2，众数为3
D.4班：总体平均值为2，总体方差为3
14.（2016内蒙古包头二模）对某两名高三学生在连续9次数学测试中的成绩（单位：分）进行统计得到如下折线图.下面关于这两位同学的数学成绩的分析中，正确的共有（ ）个.
甲同学
已同学
①甲同学的成绩折线图具有较好的对称性，与正态曲线相近，故而平均成绩为130分；
②根据甲同学成绩折线图提供的数据进行统计，估计该同学平均成绩在区间[110，120]内；
③乙同学的数学成绩与考试次号具有比较明显的线性相关性，且为正相关；
④乙同学在这连续九次测验中的最高分与最低分的差超过40分.
A.1 B.2 C.3 D.4
15.有一个容量为200的样本，其频率分布直方图如图所示，据图估计，样本数据在[8，10）内的频数为（ ）.
A.38 B.57 C.76 D.95
有关高考有套路 数学 全国卷的文章
- 详细阅读
- 详细阅读
-
数学课堂教学新思维：统计与概率教学设计案例2详细阅读
（二）教学目标复习巩固小学阶段所学的统计与概率的知识，让学生在具体情境中经历数据的整理、描述和分析的过程，感受统计在现实生活中的作用，发展统计观念。......
2023-08-03
-
统计与概率实用指南介绍详细阅读
教学难点则是使学生绘制单式折线统计图。教师投影出示：中国代表团历届奥运会金牌获奖情况统计表5-1与统计图5-3。并让学生按照教师的方法在课本上绘制折线统计图，完成后教师课件演示绘制的完整过程，同时选取部分同学绘制的折线统计图在实物展台上展示。因此，最开始，教师直接出示条形统计图，并在条形统计图的基础上，让学生认识比较折线统计图。......
2023-08-03
-
高考数学复数概念与运算详细阅读
考点1：复数的概念1.（2016全国I，2）设（1+i）x=1+yi，其中x，y是实数，则|x+yi|=（）.A.1B.C.D.2考点2：复数的四则运算2.（2017全国II，1）=（）.A.1+2iB.1-2iC.2+iD.2-i1.（2016陕西渭南一模）复数z=1-i，则z-对应的点所在的象限为（）.A.第一象限B.第二象限C.第三象限D.第四象限2.......
2023-10-15
-
数学与生活：成功学概率详细阅读
解法一 设Ai=｛第i次射击命中目标｝，B=｛至少有一次命中目标｝=A1∪A2∪A3解法二 用二项分布求解例3 某大学的社会学老教授给学生出了这样一道题目：如果一件事情成功的概率是1%，那么反复尝试100次，至少成功一次的概率大约是多少？......
2023-11-20
-
多元统计分析：误判概率与误判损失分析详细阅读
设有两个总体X1 和X2，根据某一个判别规则，把实际上为X1 的个体判为X2 或者把实际上为X2 的个体判为X1 的概率称为误判（或错判）概率．一个好的判别规则应该使误判概率最小．除此之外还有一个误判损失问题，如果把X1 的个体判到X2 的损失比X2 的个体判到X1 严重得多，则人们在作前一种判断时就要特别谨慎．比如，在药品检验中把有毒的样品判为无毒比把无毒判为有毒严重得多，因此一个好的判别规则还......
2023-11-18
-
中国概率论的发展：数学与数学家的故事详细阅读
据现有资料分析,中国概率论可划分为5 个发展阶段。许宝騄是20 世纪最富有创造性的统计学家之一,是中国最早从事概率论与数理统计研究并达到世界先进水平的优秀数学家。其研究成果已经成为概率论与数理统计理论的重要组成部分,至今“许方法”仍被认为是解决检验问题的最实用方法。此为中国概率论学科发展的重要里程碑。......
2023-11-23
相关推荐