高考数学有套路-专题集合概念与运算

2025-09-30 理论教育版权反馈

【摘要】：A.{2}B.{4，6}C.{1，3，5}D.{2，4，6}20.设全集U=R，集合A={x|x2-2x-3＜0}，B={x|x-1≥0}，则图中阴影部分所表示的集合为（）.A.{x|x≤-1或x≥3}B.{x|x＜1或x≥3}C.{x|x≤1}D.{x|x≤-1}21.已知A，B均为集合U={1，3，5，7，9}的子集，且A∩B={3}，UB∩A={9}，则A等于（）.A.{1，3}B.{3，7，9}C.{3，5，9}D.{3，9}

续表

考点1：集合的含义与表示

1.（2017全国III，1）设集合A={（x，y）|x2+y2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（　　）.

A.3　　B.2　　C.1　　D.0

考点2：集合间的基本关系

2.（2013全国I，1）已知集合A={x|x2-2x＞0}，B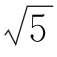={x|-＜x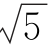＜}，则（　　）.

A.A∩B=∅　　B.A∪B=R

C.B⊆A　　D.A⊆B

考点3：集合的基本运算

3.（2017全国I，1）已知集合A={x|x＜1}，B={x|3x＜1}，则（　　）

A.A∩B={x|x＜0}

B.A∪B=R

C.A∪B={x|x＞1}

D.A∩B=∅

1.若集合A={x|x2-7x＜0，x∈N}，则B={y|N，y∈A}中元素的个数为（　　）.

A.3　　B.4　　C.1　　D.2

2.若集合M={a，b，c}中的元素是△ABC的三边长，则△ABC一定不是（　　）.

A.锐角三角形　　B.直角三角形

C.钝角三角形　　D.等腰三角形

3.已知全集A={x∈N|x2+2x-3≤0}，B={y|y∈A}，则集合B中元素的个数为（　　）.

A.2　　B.3　　C.4　　D.5

4.若集合A={-1，1}，B={0，2}，则集合{z|z=x+y，x∈A，y∈B}中的元素的个数为（　　）.

A.5　　B.4　　C.3　　D.2

5.设P和Q是两个集合，定义集合P-Q={x|x∈P，且x∉Q}，如果P={x|1-＜0}，Q={x||x-2|＜1}，那么P-Q等于（　　）.

A.{x|0＜x＜1}

B.{x|0＜x≤1}

C.{x|1≤x＜2}

D.{x|2≤x＜3}

6.已知集合A={x|log3x≥0}，B={x|x≤1}，则（　　）.

A.A∩B=∅　　B.A∪B=R

C.B⊆A　　D.A⊆B

7.已知集合A={-1，1}，B={x|mx=1}，且A∪B=A，则m的值为（　　）.

A.1　　B.-1

C.1或-1　　D.1或-1或0

8.设集合A={x∈R|＜1}，B={x∈R|2x＜1}，则（　　）.

A.A⊇B　　B.A=B

C.A⊆B　　D.A∩B=∅

9.（2015四川南充三模）设集合M满足{1，2}⊆M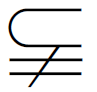{1，2，3，4}，则满足条件的集合M的个数为（　　）.

A.1　　B.2　　C.3　　D.4

10.设集合M={-1，1}，N={x|＜2}，则下列结论正确的是（　　）.

A.N⊆M　　B.M⊆N

C.M∩N=∅　　D.M∪N=R

11.设全集I=R，集合A={y|y=x2-2}，B={x|y=log2（3-x）}，则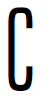IA∩B等于（　　）.(https://www.chuimin.cn)

A.{x|-2≤x＜3}

B.{x|x≤-2}

C.{x|x＜3}

D.{x|x＜-2}

12.若全集U=R，集合A={x|x2-x-2≥0}，B={x|log3（2-x）≤1}则A∩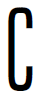UB=（　　）.

A.{x|x＜2}

B.{x|x＜-1或x≥2}

C.{x|x≥2}

D.{x|x≤-1或x＞2}

13.（2016山东日照一模）集合M={x|lg（1-x）＜0}，集合N={x|-1≤x≤1}，则M∩N=（　　）.

A.（0，1）　　B.[0，1）　

C.[-1，1]　　D.[-1，1）

14.若集合M={x|y=，N={x|x＜1}，则M∩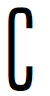RN=（　　）.

A.（0，2]　　B.（0，2）

C.[1，2）　　D.（0，+∞）

15.设集合A={x||x-1|≤2}，B={x|log2x＜2}，则A∪B=（　　）.

A.[-1，3]　　B.[-1，4）

C.（0，3]　　D.（-∞，4）

16.（2015山东日照二模）已知集合M={x|x2-4x＜0}，N={x||x|≤2}，则M∪N=（　　）.

A.（-2，4）　　B.[-2，4）

C.（0，2）　　D.（0，2]

17.设集合A={x|x2≤x}，B={x|≥1}，则A∩B=（　　）.

A.（-∞，1]　　B.[0，1]

C.（0，1]　　D.（-∞，0）∪（0，1]

18.已知集合A={x|x（x-2）≤0}，B={-2，-1，0，1，2}，则A∩B=（　　）.

A.{-2，-1}

B.{1，2}

C.{-1，0，1，2}

D.{0，1，2}

19.（2017河南焦作二模）设全集U=N，集合A={1，2，3，5}，B={2，4，6}，则图中的阴影部分表示的集合为（　　）.?

A.{2}　　B.{4，6}

C.{1，3，5}　　D.{2，4，6}

20.设全集U=R，集合A={x|x2-2x-3＜0}，B={x|x-1≥0}，则图中阴影部分所表示的集合为（　　）.

A.{x|x≤-1或x≥3}

B.{x|x＜1或x≥3}

C.{x|x≤1}

D.{x|x≤-1}

21.（2014内蒙古呼和浩特一模）已知A，B均为集合U={1，3，5，7，9}的子集，且A∩B={3}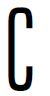，UB∩A={9}，则A等于（　　）.

A.{1，3}

B.{3，7，9}

C.{3，5，9}

D.{3，9}

高考数学有套路-专题集合概念与运算

相关推荐