图2－40叠合梁连接节点示意图1—预制梁；2—钢筋连接接头；3—后浇段正交的两个方向的梁，在交汇点进行连接，即为梁的横向连接，较为常见的是主梁和次梁之间的连接。主次梁的连接也一般采用后浇段，即主梁上预留后浇带，混凝土断开而钢筋连续，以便穿过和锚固次梁钢筋。在进行梁的横向连接时，依次将主梁、次梁安装就位，次梁的下部纵向钢筋应伸入主梁后浇段内。......
2023-10-12
工业化村镇建筑中的压弯构件与破坏机理
【摘要】：故小偏心压弯构件的最终破坏多属于压屈破坏。破坏机理重组竹压弯构件的破坏呈非线性渐进破坏特性。图6－20压弯构件的塑性变形及截面应变分布示意图因此，梁—柱的最大挠曲变形可看成由两部分组成：由极限荷载Pu产生的理想弹性位移δe；外荷载保持不变，由塑性铰转动产生的塑性变形δp。
由于竹、木复合材料在细观构造和宏观性能等方面的相似性，目前的重组竹结构设计计算均参考木结构设计规范的计算方法。然而，国内外现行木结构规范均采用线弹性理论分析梁—柱构件的荷载响应，以最大应力理论为破坏准则，未考虑材料的非线性特性。如我国现行国家标准《木结构设计规范》（GB 50005—2003）、欧洲规范Eurocode和美国木结构设计手册NDS—2015给出的压弯构件强度验算公式分别为将压弯构件的响应简化为轴向力与弯矩各自响应的线性叠加，忽略了压弯耦合效应和非线性效应，因而，只适用于比例极限承载力校核；加拿大木结构设计手册考虑了压弯耦合效应，但该公式仍未考虑木材受压非线性本构关系，并沿用最大应力理论作为破坏准则，没有反映压弯构件的破坏机理，因而，构件承载力的计算过于保守。
1.破坏形态与破坏机理
（1）破坏形态
根据试件偏心距不同，压弯构件的破坏主要分为两类，即小偏心受压破坏和大偏心受压破坏。
小偏心受压破坏特征表现为：构件跨中受压区外边缘竹纤维束发生压屈变形，竹束向外鼓起，其压应变达到材料极限压应变；而受拉区的竹纤维束尚处于工作状态，没有达到极限强度，未能发挥竹纤维良好的力学性能。故小偏心压弯构件的最终破坏多属于压屈破坏。由于在初始偏心距较小的情况下才发生小偏心受压破坏，故本节在后面的压弯构件强度与变形计算中，对于小偏心构件不作讨论。
大偏心受压破坏特征表现为：多数构件跨中受拉区外边缘竹纤维束发生拉断破坏，这与梁的弯曲破坏现象类似。首先因构件受压，使内部微裂纹开始发展，受压区竹束先发生屈曲；然后随荷载增加，受拉区纤维束之间发生界面破坏，产生宽度较大的纵向裂纹，将竹构件逐步分割成若干竹束；最终构件受拉区纤维束拉断，梁—柱丧失承载能力。故大偏心受压破坏多属于构件的弯曲破坏。
（2）破坏机理
重组竹压弯构件的破坏呈非线性渐进破坏特性。首先构件上部纤维受压屈曲；其次是受拉区纤维束之间发生界面分离，形成平行于纤维方向的纵向裂纹，这些裂纹随外荷载的增加不断扩展，宽度逐渐增大；最后下部纤维束拉断，构件丧失承载能力。
2.承载力计算
如图6－19（a）所示，一根长为l的竹柱两端受偏心压力P 的作用，初始偏心矩为e0，构件在偏心作用下将会产生侧向挠曲变形ω（x），故柱截面弯矩除了端部初始弯矩M0＝Pe0外，受侧向挠曲变形影响，会产生附加弯矩Ma＝Pw（x）。因ω（x）在不断变化，则构件的附加弯矩Ma也在变化，这就是所谓的梁—柱构件轴力与弯矩的相关性，即压弯构件自身挠曲引起的二阶效应（p－δ效应）。因此，在偏心受压构件的整个受力过程中，同样需考虑材料拉压的不同性质，以及材料的本构关系。实际上，压弯构件的承载力计算（即梁—柱）可看作是在受弯构件基础之上考虑轴向力的作用，其分析方法与受弯构件相同。
若构件最终产生的侧向变形为δ，则跨中截面的弯矩为M＝P（e0＋δ）。根据力的平衡与弯矩平衡方程，得
式中，e＝e0＋δ。构件的截面应力分布与受弯构件相同，则将式（6－8）代入式（6－25），得
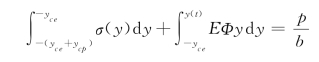
此处，受压轴力P 为负值。令σn＝p／bh，则
利用式（6－14）对α的定义，则式（6－27）可写成
结合式（6－11）、式（6－12）和式（6－25），则可求出yt、yce、ycp的值，即
根据式（6－26），极限状态下的梁—柱截面弯矩可表示为
式中，Φu为压弯构件极限状态下的弯曲曲率，且第三项为截面塑性受压区产生的弯矩。结合式（6－26），可求得塑性受压区的弯矩为
式中：Φu可依据极限状态下受拉区的应力—应变仍服从胡克定律，求得
(www.chuimin.cn)
结合弹性阶段截面正应力产生的弯矩，则压弯构件的极限弯矩为
故压弯构件极限承载力为
式中：eu＝e0＋δu，δu——极限状态下压弯构件的侧向挠度。
3.变形分析
假设当梁—柱偏心力超过临界值时，只有达到临界状态的截面及其附近位置进入塑性阶段，构件的其他部位实际上还处于弹性阶段。故可以将压弯杆件的临界断面看作是一个塑性铰，即极限状态下，梁—柱是带有塑性铰的弹性杆件，以此求最大挠曲变形。
图6－20给出了构件临界断面的侧向变形及其截面应变分布图，A→B显示构件从弹性状态到极限状态的真实路径，若按照此路径求解构件塑性变形的发展，会非常困难，因此将此路径简化为C→D，便于模型计算。首先从加载初期到达假定的理想临界状态，如图6－20（d）所示，假设杆件已到达极限承载力，且杆件受压呈线弹性；然后保持荷载不变，由塑性铰转动，使杆件由理想状态转变到真实的极限状态，如图6－20（e）。
图6－20 压弯构件的塑性变形及截面应变分布示意图
因此，梁—柱的最大挠曲变形可看成由两部分组成：（1）由极限荷载Pu产生的理想弹性位移δe；（2）外荷载保持不变，由塑性铰转动产生的塑性变形δp。则杆件的极限位移可表示为
根据梁—柱理论微分方程求解，由极限荷载Pu产生的理想弹性位移δe为
式中：
。将x＝l／2代入式（6－35），得
由平截面假定，ε＝Φy，以及几何关系，可得理想弹性状态和极限状态下构件曲率分别为
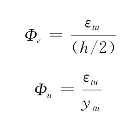
故由塑性铰产生的曲率增量为
假设取构件的微段ds，对应假定第二部分所产生的塑性铰转动量为
则塑性铰产生的总转动量为
式中：lp——塑性铰长度。构件端部产生的塑性转角位为θp／2，根据小变形理论以及忽略高阶微分影响，由理想的塑性铰转动产生的塑性位移为
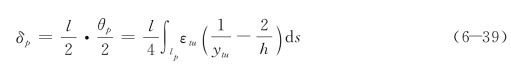
式中：ytu是由σn＝pu／A 代入式（6－29a）求得。因为塑性铰长度比较小，可假定沿塑性铰长度曲率均相同，则式（6－39）可写为
有关工业化村镇建筑的文章
- 详细阅读
-
工业化村镇建筑中的木结构材料特性详细阅读
结构中的承重构件多采用针叶材。木材干湿的程度通常用干缩率表示。体积干缩率影响木材的密度。木材的纵向干缩率很小，一般为0.1%左右，弦向干缩率为6%～12%，径向干缩率为3%～6%，径向与弦向干缩率之比一般为1∶2，径向与弦向干缩率的差异是造成木材开裂和变形的重要原因之一。气干密度则为生产计算木材气干时质量的依据。......
2023-10-12
-
工业化村镇建筑：抗震规定详细阅读
灾害调查和事故分析表明，结构布置方案对建筑物的安全有着决定性的影响。秸秆板轻钢发泡混凝土剪力墙结构承受的荷载应符合现行国家标准《建筑结构荷载规范》及相关标准的规定；地震作用应符合现行国家标准《建筑抗震设计规范》的有关规定。在抗震设防区里，当房屋采用秸秆板轻钢发泡混凝土剪力墙设计时，房屋应满足设防烈度地震作用下的抗震承载力要求。......
2023-10-12
-
冷弯薄壁型钢在工业化村镇建筑中的特点详细阅读
随着钢结构的结构形式日趋广泛，高效、经济的冷弯薄壁型钢在建筑业尤其是轻钢房屋的建设中应用尤其突出。建筑结构中的冷弯薄壁型钢有如下优点：通过冷成型加工可经济地得到需要的截面形状，进而获得令人满意的强度质量比，以节约用钢量。与木材和混凝土等其他材料相比，冷弯薄壁型钢结构构件具有以下特性：质量轻、强度高、刚度大。......
2023-10-12
-
轻型竹结构在工业化村镇建筑中的应用详细阅读
图6－23轻型竹结构墙体如图6－23所示，轻型竹结构墙体是由构件断面较小的规格胶合竹材均匀密布形成由墙骨柱、顶梁板、底梁板和过梁组成的棱骨架，然后钉上竹胶合板组成的一种结构形式，类似北美木结构中的二乘四构造。图6－24二层楼盖施工现场图6－25竖起墙体轻型竹结构的主要结构构件一般在工厂预制再搬运至现场拼装。......
2023-10-12
-
工业化村镇建筑的叠合板构造详细阅读
在此，以常规叠合板为例介绍其构造要求，对于其他形式的叠合板，可参照进行设计。当采用悬挑叠合板，悬挑叠合板的上部纵向受力钢筋锚固在相邻叠合板的后浇混凝土范围内时，应在悬挑叠合板及其钢筋的锚固范围内配置截面抗剪构造钢筋。叠合板之间的接缝，可以采用两种构造措施：分离式接缝和整体式接缝。试验研究表明，这种构造形式的叠合板整体性较好。......
2023-10-12
-
工业化村镇建筑：定义与简介详细阅读
在《村镇建筑抗震鉴定与加固技术规程》征求意见稿中规定，既有村镇建筑主要是指乡镇与农村中层数为一、二层的未进行抗震设防的一般建筑。在《村镇住宅设计规范》征求意见稿中规定，村镇住宅是供村庄、集镇中的居民家庭居住使用的建筑，未规定层数。根据调研发现，目前我国的村镇建筑的主体结构依旧以砖混和木结构为主，同时在建筑风格上具有鲜明的地域化和地区化特色。......
2023-10-12
-
工业化村镇建筑中的屋盖工程与分析方法详细阅读
目前，对于工业化木结构房屋的系统研究仍处于起步阶段，木屋盖的基本性能需要结合试验研究和实际工程来具体分析。屋盖结构分析方法一般可以采用两种主要的分析方法，一种是基于单榀屋盖的二维分析方法，另一种是系统分析方法。若覆面板的厚度小于10mm，可由50 mm 长的麻花钉或普通圆钢钉、40 mm 长的U 形钉或45mm长的螺钉将覆面板和屋架钉接。......
2023-10-12
相关推荐