图4－29是现场吊装和安装楼盖施工过程图。图4－26工厂内楼盖预制施工工艺流程图图4－27楼盖轻钢龙骨拼装和单面覆板图4－28浇筑发泡混凝土和覆盖秸秆板图4－29楼盖的吊装和固定连接值得注意的是，在工厂里对楼盖的制作过程中，秸秆板的预处理是一个重要的施工过程。当发泡混凝土达到初凝后，撤除薄膜并覆盖另一侧秸秆板，完成房屋楼盖结构部分的制作。......
2025-09-30
顺纹应力—应变关系及其工业化村镇建筑设计
【摘要】：研究发现，重组竹顺纹受拉、顺纹受剪和垂直纹理方向受剪应力—应变关系呈直线型，应力—应变方程满足线弹性胡克定律。顺纹分段型应力—应变关系重组竹顺纹受压和垂直纹理平面纯剪应力—应变曲线在加载初期呈线性关系，当荷载超过比例极限后，曲线逐渐偏离原来的线性关系。试验数据统计分析表明，顺纹受压应力—应变曲线的非线性段可以采用二次曲线模拟。
工程竹的应力—应变关系是研究和分析竹构件力学性能的主要材性依据。工程竹的应力—应变关系主要包括横纹和顺纹的拉压、受剪应力—应变关系。因梁柱构件承载力与变形计算一般仅涉及使用工程竹的顺纹力学性能，故本书以重组竹为例，介绍工程竹的应力—应变关系。
1.重组竹材料参数
图6－15 重组竹材料方向定义
重组竹纤维沿材料纵向相互平行，沿横向随机分布，故可以将其理想化为横观各向同性正交异性复合材料。根据图6－15所示的笛卡尔坐标系定义重组竹材料3个坐标轴方向，1轴代表重组竹的顺纹方向，2、3轴代表重组竹的两个横纹主方向。
重组竹的材料参数可采用双下标表示，第一个下标表示该参数所在平面的外法线方向，第二个下标表示该参数的方向。根据横向同性假定，重组竹材料参数包括6个强度参数、3个弹性模量、3个剪切模量和2个泊松比。6个强度参数分别是顺纹和横纹方向的拉、压强度以及法线方向为1轴和3轴的平面内剪切强度。
重组竹的线弹性本构方程可表示为
式中：ε——应变列向量，
；
σ——应力列向量，
；
C——柔度矩阵，各弹性参数均可通过试验测得；
E11、E22、E33——重组竹顺纹与横纹弹性模量；
G23、G13、G12——各主平面的剪切模量；
ν31、ν32、ν33——各主平面的泊松比。
2.重组竹应力—应变关系
重组竹作为纤维增强多相复合材料，其复杂的顺纹与横纹拉、压和剪切本构关系，使竹构件的非线性响应、破坏机理与一般均质材料或理想弹塑性材料有本质区别。即使材料在宏观上处于单轴受力状态，其内部也会因纤维与基体力学性能的极大差异、纤维与受力方向的偏差以及材料初始裂纹的存在而产生复杂应力状态，从而产生纤维屈曲、断裂、与基体剥离、基体压溃和原始裂纹扩展等复杂响应。
研究发现，重组竹顺纹受拉、顺纹受剪和垂直纹理方向受剪应力—应变关系呈直线型，应力—应变方程满足线弹性胡克定律。顺纹受压应力—应变曲线呈分段型，在加载初期呈线性关系，当荷载超过比例极限后，曲线逐渐偏离原来的线性关系，进而表现出材料的非线性应力—应变关系。
（1）顺纹直线型应力—应变关系
顺纹直线型应力—应变关系有顺纹受拉（方向1受拉）、顺纹受剪（1～2或1～3平面内沿方向1受剪）。这类应力—应变方程满足线弹性胡克定律，可分别表示为：
①顺纹受拉
(https://www.chuimin.cn)
②顺纹受剪
式中：Gij——剪切模量；
E11——杨氏模量。
（2）顺纹分段型应力—应变关系
重组竹顺纹受压和垂直纹理平面纯剪应力—应变曲线在加载初期呈线性关系，当荷载超过比例极限后，曲线逐渐偏离原来的线性关系。这类曲线需采用分段型曲线表达。
重组竹顺纹受压应力—应变曲线有明显的比例极限、峰值应力及应变极限；曲线也相应分为3段，即线弹性段、非线性强化段和非线性软化段。试验数据统计分析表明，顺纹受压应力—应变曲线的非线性段可以采用二次曲线模拟。因此，将重组竹的纵向单轴应力—应变关系表示为如下分段函数：
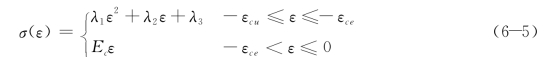
式中：λi（i＝1，2，3）——待定系数。考虑应力—应变曲线连续性条件，得：
式（6－6c）表示应力达到最大值后，应力—应变关系曲线由非线性强化阶段转入软化阶段的趋势。求解式（6－6）得待定参数：
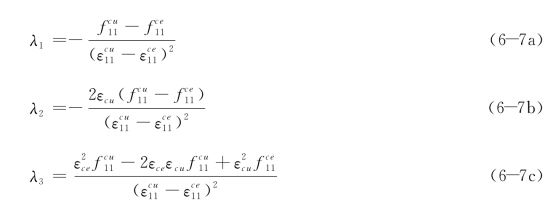
式中：
——1方向的受压比例极限应力与应变；
——1方向的受压极限应力与应变。
重组竹顺纹单轴、顺纹受剪作用下的应力—应变方程可汇总于表6－2。
表6－2 重组竹顺纹应力—应变关系
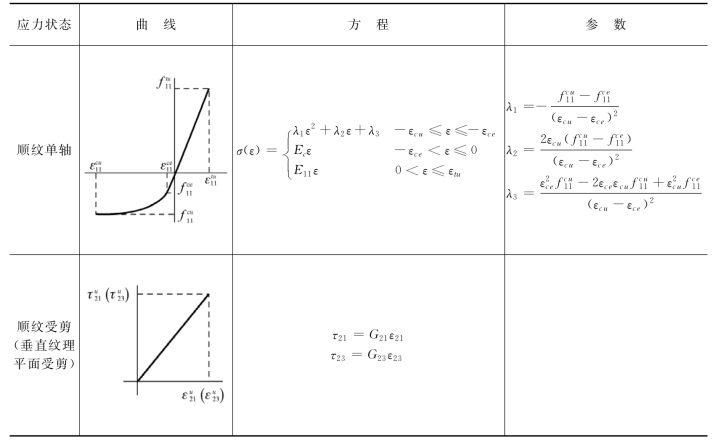
表中：Eii——i方向的杨氏模量，i＝1，2，3；
Gii——i方向的剪切模量，i＝1，2，3；
——i方向的受拉极限应力和极限应变；
——i方向的受压比例极限应力与应变；
——i方向的受压极限应力和应变；
λi（i＝1，2，3）——非线性阶段应力—应变关系二次曲线参数。
相关文章
- 详细阅读
-
上连杆应力应变分析优化详细阅读
上连杆在框架断路器操作机构的连杆结构中具有典型性，因此选择框架断路器上连杆为研究对象，使用ADAMS软件和ANSYS有限元软件计算机构运动过程中上连杆的应力应变，并比较ADAMS软件模态综合法和ANSYS有限单元法的计算结果。图3-8显示了ANSYS有限元软件有限单元方法计算出的t=0.0274s时刻，上连杆应力应变分布云图和3567号节点的应力应变时间历程曲线，可见上连杆的应力集中主要发生在内侧弯曲处，并与ADAMS软件刚柔耦合方法的计算结果吻合较好。......
2025-09-29
-
工业化村镇建筑楼盖系统构造详细阅读
拼接长度不应小于150 mm，腹板之间的连接至少每边用4个ST4.2的自攻螺钉，每侧翼缘至少用4个ST4.2的自攻螺钉。具体设计时，在安全可靠的前提下，楼盖系统构造也可以采用其他的连接形式和构造方法，并按相关的现行国家标准设计。......
2025-09-30
-
工业化村镇建筑介绍及特点详细阅读
由于建筑工业化生产方式可以较大幅度地提升劳动生产率，但是我国建筑业一直都是劳动密集型产业，且一直享受着廉价劳动力的优势，又能带来巨大就业，因此，建筑工业化的推动力不强。浙江、江苏、山东等诸多省份也分别出台了建筑工业化相关文件，大力推行建筑工业化。目前国外发达国家早已步入了工业化建筑的时代。由此可见建筑工业化与村镇建筑的结合是必然趋势。......
2025-09-30
-
工业化村镇建筑：叠合梁构造详细阅读
图2－36叠合框架梁截面示意图1—后浇混凝土叠合层；2—预制梁；3—预制板叠合梁施工时，先将叠合梁的预制部分吊装就位，然后安装叠合板预制板，将预制板侧的钢筋伸入梁顶预留空间。图2－38采用整体封闭箍筋的叠合梁试验表明，键槽的抗剪承载能力要大于粗糙面，且易于控制加工质量和检验。图2－39梁端键槽构造示意图1—键槽；2—梁端面......
2025-09-30
-
总体构造要求-工业化村镇建筑详细阅读
我国早期的工程实践中，装配式结构在地震作用下产生了较多的损伤，严重丧失整体性，或者造成整体结构的倒塌，或者局部构件的连接不足，导致掉落造成生命财产的惨痛损失。正是由于这些教训，长期以来人们产生了“装配式结构整体性不高”的印象，限制了装配整体式建造模式的应用和发展。因此，构造措施必须充分考虑工地现场的安装可行性，对可能发生的意外情况做好预案。......
2025-09-30
-
应力/应变测试简介详细阅读
预计出最大应变力的变形位置及变形形式，根据测试要求选定测试点。2）如果最大应力点的位置难以确定，或者为了了解截面应力分布规律和曲线轮廓段主应力过渡情况，可在截面上或者过渡段上比较均匀地布置5～7个测点。在已知主应力方向的情况下，应尽量保证贴片方向的一致性。......
2025-09-29
-
工业化村镇建筑：定义与简介详细阅读
在《村镇建筑抗震鉴定与加固技术规程》征求意见稿中规定，既有村镇建筑主要是指乡镇与农村中层数为一、二层的未进行抗震设防的一般建筑。在《村镇住宅设计规范》征求意见稿中规定，村镇住宅是供村庄、集镇中的居民家庭居住使用的建筑，未规定层数。根据调研发现，目前我国的村镇建筑的主体结构依旧以砖混和木结构为主，同时在建筑风格上具有鲜明的地域化和地区化特色。......
2025-09-30
相关推荐