斜坡软弱地基路堤稳定性极限平衡法分析的研究成果

斜坡软弱地基包括山区丘间槽谷坡洪积软弱土地基、非沉积型斜坡软弱地基、湖泊相软土边缘地基和斜坡松散堆积体地基等，类型多样，成因复杂[2]。另外，为避免长距运输优质填料，路堤填料多就地取材，如移挖作填或利用隧道弃渣，来源广泛；丰富的地下水是形成斜坡软弱地基的重要条件[47]，而地下水位受降雨、山洪暴发等影响波动较大；从工程处治措施看，微型桩已成功应用于斜坡软弱地基路堤工程实践，但可能受粗放式地勘、设计、施工等的影响，导致桩距、桩体抗剪强度等核心参数与理想状况有所出入；路堤顶部受拉后形成张拉裂缝容易充填水分，而水分充填量也存在着波动性；西南地区还频发地震，各地地震烈度不一：这些都充分说明，简单地采用确定性分析获得某一个安全系数，进而直接评价斜坡软弱地基路堤稳定性的方法并不科学合理。作为传统确定性稳定安全系数分析的有益补充，考虑以上各种变量随机性的可靠性分析应在斜坡软弱地基路堤稳定性极限平衡法研究中给予足够重视。

为此，本节基于可靠度，采用加拿大Rocscience Inc.开发的2D垂直条分极限平衡法软件Slide，就路堤与斜坡软弱层土体材料属性、路堤顶部张拉裂缝水分充填量、微型桩纵向间距与抗剪强度工程处治属性及地下水位与水平向地震荷载环境属性等变量的随机性，对斜坡软弱地基路堤稳定性影响开展概率分析和敏感性分析，提出实际工程提高路堤稳定性的有效对策，并尝试阐释室内斜坡软弱地基路堤土工离心模型试验出现失稳破坏现象的机理。

3.3.5.1　分析原理及软件简介

计算分析所选用的Slide软件拥有强大的可靠度分析功能，包括概率分析和敏感性分析，其中：概率分析需设定材料属性、支护属性、荷载、水位等输入参数的统计分布规律，并通过安全系数平均值、破坏概率PF、可靠度指数RI等描述分析结果；而敏感性分析则可确定输入参数的变化对边坡稳定性的影响大小，其分析流程为对于给定的敏感性分析变量，程序将其在值域内分为50个区间，通过确定性分析，确定最不利滑动面，然后使用上述50个值计算安全系数。

概率分析和敏感性分析的差别在于：概率分析根据分布函数对随机变量抽样，而敏感性分析是在一个由最大值和最小值所定义的区间内进行取值；概率分析可以拥有全部随机样本，而敏感性分析每次迭代只允许存在一个变量变化，其他参数作为常量（确定值），一般取均值；概率分析通过确定参数的标准差来确定其相对最大值和最小值，而敏感性分析只需要确定参数的最大和最小值。通过Slide可以同时开展概率分析和敏感性分析，也可以二者分开单独开展任一种分析。概率分析主要获得边坡的破坏概率，而敏感性分析则确定具体参数对边坡安全系数的影响权重。

3.3.5.2　分析模型建立

如图3-67所示，建立单线铁路斜坡软弱地基路堤的极限平衡法分析模型。该模型能同时考虑路堤与斜坡软弱层材料属性、路堤顶部张拉裂缝水分充填量、微型桩属性、地下水位与水平向地震荷载等环境属性的变异性。其中地层坡度为1∶10，路堤顶面宽7.5 m，路堤边坡坡比为1∶1.5，路堤中心线填高为7.88 m，斜坡软弱层厚6 m，其下为刚硬层。

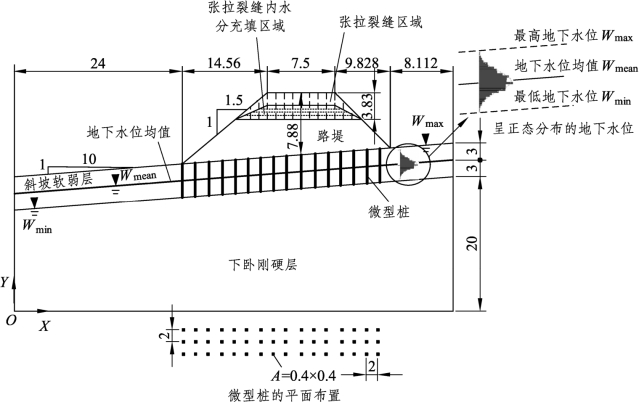
图3-67　斜坡软弱地基路堤Slide模型示意（未按比例，单位：m）

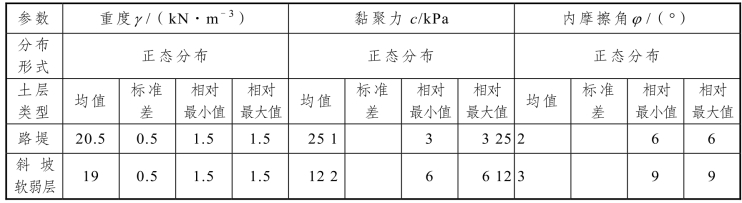
各土层材料均采用Mohr-Coulomb强度模型，暂只考虑路堤、斜坡软弱层土体材料的变异性。参考文献[48，49，29，27]，假定概率密度分布函数为正态分布，表3-16给出了反映路堤、斜坡软弱层土体材料变异性的计算参数，包括均值、标准差、相对最小值及相对最大值，并假定这两层土体的黏聚力和内摩擦角相关系数均为－0.5，即黏聚力和内摩擦角为负相关，土体材料黏聚力较低时，内摩擦角往往较大，反之亦然，从而使样本采样更具合理性。下卧刚硬层的重度为20.5 kN/m3，黏聚力为24 kPa，内摩擦角为25°。

表3-16　路堤与斜坡软弱层土体材料参数

从最不利角度出发，假定路堤顶部产生了张拉裂缝，其深度的计算采用 Abramson等[50]提出的经验公式计算得到：

其中：zc表示张拉裂缝深度（m）；c、γ 、φ分别表示路堤填料黏聚力（kPa）、重度（kN/m3）和内摩擦角（°）。

将表3-16中路堤重度、黏聚力、内摩擦角的均值代入，即可得到本模型的张拉裂缝深度为3.83 m。不妨取张拉裂缝内水分充填量平均占裂缝总体积的50%，假定水分充填量变化服从正态分布，标准差为16%，相对最小值为48%，相对最大值为48%。

从路堤下坡脚处开始向上，斜坡软弱层内实施预制的C20混凝土微型桩，桩身横截面尺寸为0.4 m×0.4 m，呈桩距2 m方形布置，路堤横断面方向共布置16根桩，桩长6 m。根据C20混凝土的抗压强度及其与抗剪强度之间的关系[51]，确定每根微型桩所能承受的最大剪力，进而确定微型桩的抗剪强度。假定微型桩抗剪强度和纵向间距的变化均服从正态分布，表3-17给出了微型桩计算分析参数。

表3-17　微型桩计算分析参数

地下水位平行于地层坡面，且平均处于斜坡软弱层的中部，并假定地下水位只在斜坡软弱层内上升或下降。地下水位的变化服从正态分布，设均值为0.5，标准差为0.15，相对最小值为0.45，相对最大值为0.45。

西南地区地震烈度一般在6度或者7度以上，参考《铁路工程抗震设计规范》（GB 50111—2006）[52]，采用设计地震的地震动峰值加速度，假设水平方向存在一个大小为0.2g的加速度，且该加速度变化服从正态分布。为了使加速度变化区间涵盖烈度6～9度，设标准差为0.066g，相对最小值为0.198g，相对最大值为0.198g。

3.3.5.3　计算分析方法

如前所述，Slide软件概率分析提供了全局最小分析、整体边坡分析两种方法，本节暂以全局最小分析为准。即首先使用确定性方法进行分析，得出最危险滑动面，然后用采样的各样本参数对该滑动面进行计算，执行次数为样本总数，最后统计计算结果，定义破坏概率PF为安全系数小于1的样本数与总样本数之比。需要注意的是，不同的分析方法（如简化Bishop法、简化Janbu法）可以得到不同的最不利滑动面，程序对其分别独立分析，最后以最不利滑动面的破坏概率表征整个路堤的破坏概率。

采用简化Bishop法和简化Janbu法，垂直条分所建立的模型。采用Monte-Carlo方法取样，样本数量为20 000。搜索方式为网格搜索（Grid Search），即在开始计算前，自行输入搜索网格的大小M×N（本模型采用40×40的搜索网格），网格线的交点即为圆心。Slide自动根据设立的模型边界来确定每个圆心的半径，然后按照半径增加量加上1作为该圆心搜索的圆弧数，此半径增加量是每个圆心最小半径与最大半径的间隔数。搜索网格的位置应适当，以确保计算得到的最小安全系数的圆心大致处于搜索网格的中心。

3.3.5.4　主要计算结果分析及讨论

1.概率分析

采用简化Bishop法和简化Janbu法计算得到的宏观结果如图3-68所示。可见，两种方法所获得的最危险滑动模式均大致表现为路堤顶部垂直、路堤下部及斜坡软弱层内呈圆弧状，滑动面底与斜坡软弱层底略相切，未深入至下卧刚硬层内。滑动面在路堤顶部呈垂直状分布，这应与前文假定路堤顶部存在着张拉裂缝直接相关。简化Bishop法所获得的滑动面分布范围明显大于简化Janbu法。显然，因断面几何对称性的丧失，滑动面向下坡脚方向倾斜，这意味着实际工程中可适当于下坡脚方向斜坡软弱地基内加密微型桩以提高路堤稳定安全性。

表3-18给出了两种方法计算结果的对比，其中Fsdeterministic为采用确定性分析方法计算得到的稳定安全系数；Fsmean为各样本对全局最小滑动面作确定性分析得到的稳定安全系数的平均值；PF为稳定安全系数小于1的样本的数量与总样本数量之比即破坏概率；RInormal、RIlognormal分别为稳定安全系数服从正态分布、对数正态分布时的可靠度指数。可靠度指数RInormal和RIlognormal分别可用下述两个公式[46] 计算得到：

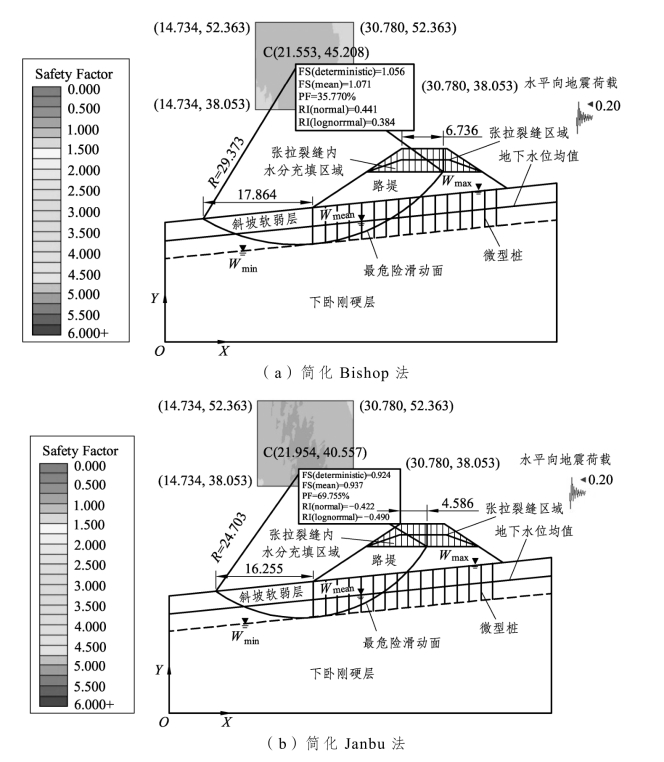
图3-68　两种计算方法宏观计算结果（尺寸单位：m）

式中：是安全系数的平均值；是安全系数的标准差；V是安全系数的标准差与安全系数均值的比值，即V=。

表3-18　简化Bishop法和简化Janbu法计算结果对比

简化Bishop法确定性安全系数大于1，而简化Janbu法确定性安全系数小于1，这是由于简化Janbu法假设土条间的作用力的合力总是位于距滑面1/3处，计算得到的抗滑力矩偏小；两者稳定安全系数的平均值均大致接近于各自确定性安全系数；简化Janbu法破坏概率PF比简化Bishop法增大约95%。简化Bishop法计算的安全系数虽然大于1，但两个可靠度指数都远小于3，可认为路堤的稳定性不满足要求。而简化Janbu法计算的安全系数小于1，同时两个可靠度指数也远小于3。由于采用简化Janbu法计算得到的安全系数Fsmean 小于1，所以两个可靠度指数都是负数。

本模型取样样本数量为20 000，图3-69是分别采用简化Bishop法和简化Janbu法计算得到的样本结果统计分析收敛曲线。采用两种方法得到的统计分析收敛曲线最后均趋向于平缓，末端所对应的破坏概率PF分别是35.770%、69.755%，与计算结果一致，这说明样本数量足够多，计算精度满足要求。

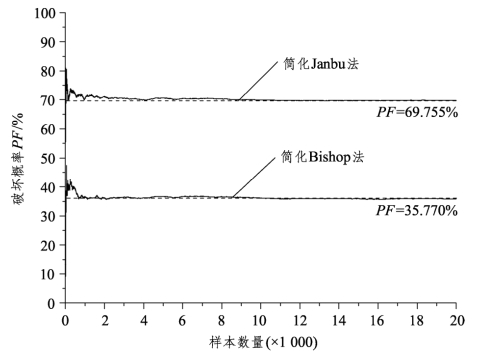
图3-69　统计分析收敛曲线

图3-70是20 000个抽取的样本通过简化Bishop法和简化Janbu法分别计算得到的安全系数绘制成的柱状图，反映了各个安全系数段占整个样本的出现频率。其中黑色柱体表示的是安全系数小于1的样本。黑色柱体面积与黑白两色柱体面积总和之比即为破坏概率。图上的曲线表示安全系数呈对数正态的最佳分布。

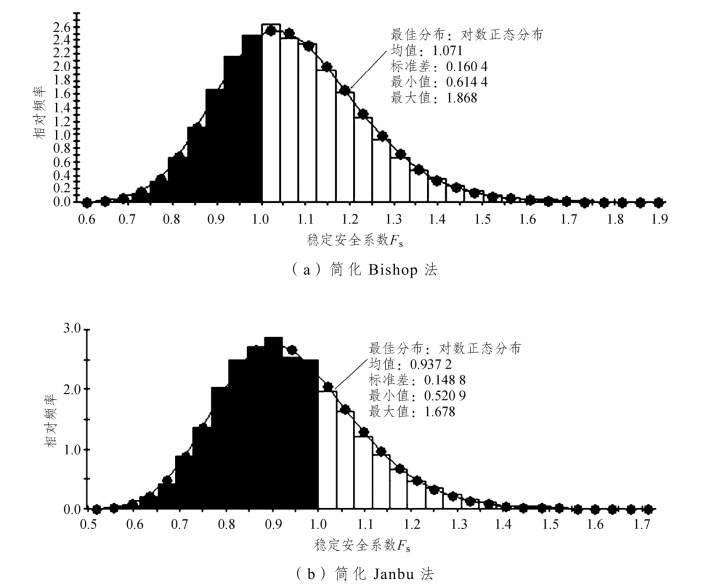
图3-70　两种方法稳定安全系数概率密度分布

图3-71所示是分别用简化Bishop法和简化Janbu法计算得到的累计概率与安全系数的关系曲线，每一个横坐标安全系数都对应一个累计概率，表示的是小于等于该安全系数所对应的概率值，当横坐标安全系数等于1时对应的即为破坏概率。采用简化Bishop法和简化Janbu法计算得到的破坏概率分别为35.770%和69.755%，如图3-71所示。通过该图，可以确定任何一个安全系数对应的累计概率，为实际工程设计时提供帮助。

图3-71　稳定安全系数与累计概率的关系曲线

图3-72分别给出了路堤和斜坡软弱层的内摩擦角与黏聚力相关性的散布图，图中每个十字符号表示一个样本，其对应着一组c和φ 值。散布图线性拟合后相关系数分别为－0.494 248和－0.492 813，接近于－0.5，这与前文设定在Mohr-Coulomb强度模型材料前提下，路堤与斜坡软弱层的内摩擦角φ 和黏聚力c存在－0.5的负相关性吻合，同时也说明抽取的样本数量相对充裕。显然，如果相关系数越接近于－1，则散点越相对集中分布于所拟合的直线两侧。因进行概率分析时，各参数的变化区间不同，两条拟合直线的斜率有所差异。

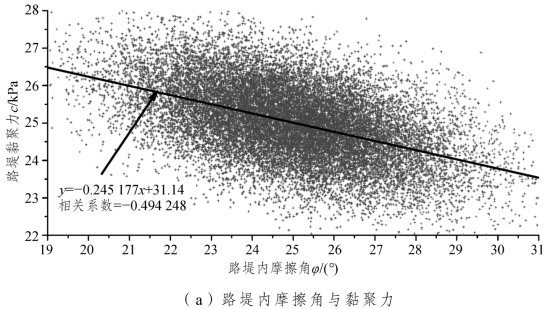
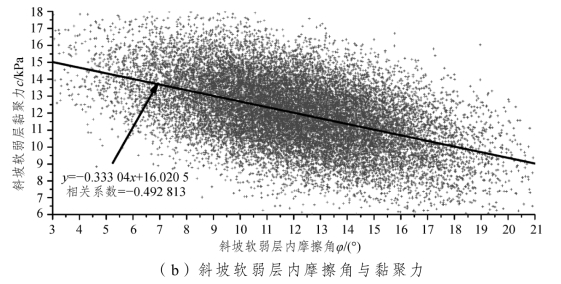
图3-72　路堤和斜坡软弱层的内摩擦角和黏聚力相关性的散布

2.敏感性分析

采用简化Bishop法和简化Janbu法得到的敏感性规律一致，为节约篇幅，只讨论简化Bishop法的敏感性分析结果，如图3-73所示。因各参数的量纲不同，横坐标用各参数的变化区间来表示，整个变化区间定义为0～100%。可见，斜坡软弱层内摩擦角、斜坡软弱层黏聚力、路堤内摩擦角、路堤黏聚力及微型桩抗剪强度与稳定安全系数Fs正相关，即这些参数变大，稳定安全系数Fs增加，路堤稳定性提高。而路堤重度、斜坡软弱层重度、微型桩纵向桩间距、水平向地震荷载、地下水位及张拉裂缝水分填充量与稳定安全系数Fs呈负相关，这些参数变大，稳定安全系数Fs相应减小，路堤稳定性降低。

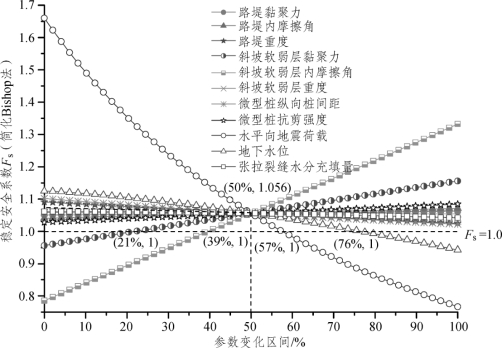
图3-73　各不确定性因素对安全系数的敏感性分析结果

水平向地震荷载、斜坡软弱层内摩擦角、斜坡软弱层黏聚力以及地下水位与稳定安全系数的敏感性曲线较陡，斜率的绝对值较大，即这几个不确定性因素对稳定安全系数的影响权重较大；微型桩纵向桩距、桩体抗剪强度、路堤重度和张拉裂缝水分填充量与稳定安全系数的敏感性曲线的斜率较小，这几个不确定性因素对路堤稳定安全系数的影响一般；路堤内摩擦角、路堤黏聚力和斜坡软弱层重度与稳定安全系数的敏感性曲线相对比较平缓，斜率近乎为零，可视这几个不确定性因素对稳定安全系数的影响甚微。

图中各曲线均相交于一点，该点坐标为（50%，1.056）。在进行敏感性分析时，只有一个参数发生变化，其他的参数保持为均值不变，当该参数变化到均值时，计算得到的稳定安全系数sF即与概率分析所获得的确定性安全系数一样。如果各参数均保持均值，则计算得到稳定安全系数sF都是1.056。

取安全系数Fs＝1.0，绘制一条横线，该横线将与水平向地震荷载、斜坡软弱层内摩擦角、斜坡软弱层黏聚力、地下水位的敏感性曲线分别大致相交于（57%，1）、（39%，1）、（21%，1）、（76%，1），其他参数的敏感性曲线均未与该横线相交，这说明除了水平向地震荷载、斜坡软弱层内摩擦角、斜坡软弱层黏聚力和地下水位这4个不确定性因素外，其他的不确定性因素在单独变化时，路堤稳定安全系数Fs始终大于1。而这4个不确定性因素在单独变化时，路堤会在稳定与破坏两种状态之间转换，如：水平地震荷载超过57%，即从稳定变化为破坏；而斜坡软弱层内摩擦角超过39%，即从破坏变化为稳定。

根据以上敏感性分析结果，在实际工程中可尝试采取“扬正抑负淡缓”的宏观处治原则，即提高正相关因素量值，削减负相关因素量值，淡化相对平缓因素的量值，以有效、经济地提高路堤稳定性。具体工程对策为：既然地震是不可避免的偶发自然灾害，宜尽量采取绕避措施；路堤可适当选用重度偏低的填料，尤其是路桥（涵）过渡段，路堤内摩擦角和黏聚力对稳定性影响权重较小，可不予严格控制；斜坡软弱层重度对路堤稳定性影响不大，而内摩擦角和黏聚力对稳定性影响很大，宜采取碎石桩等复合地基处理方案，只要确保内摩擦角增量对稳定性的提升效应大于因黏聚力下降、重度增加而造成的路堤稳定性下降的负面效应，即可达到提高路堤稳定性的目的；微型桩应在确保选材精良、抗剪强度良好的基础上，精心施工；同时做好各种防排水措施，尽量降低地下水位；对于路堤顶部出现的张拉裂缝，应及时设法封堵，避免水分聚集于张拉裂缝内。

3.3.5.5　实例应用

下面选用一实例来讨论基于可靠度的斜坡软弱地基路堤稳定性极限平衡法的成功应用。魏永幸[24]等开展了水平软弱地基路堤和1∶10的斜坡软弱地基路堤的土工离心模型试验，所对应的原型路堤顶面宽7.5 m，路堤边坡坡比为1∶1.5，水平软弱地基路堤中心线填高为8 m，保持路堤顶面宽仍为7.5 m等截面换算得出斜坡软弱地基路堤的中心线填高为7.88 m，斜坡软弱层厚6 m，其下为刚硬层。参照有关文献对模型试验后的土体参数进行修正的结果，取各土层参数如表3-19所列，其中下卧刚硬层暂不考虑其材料变异性，其重度为20.5 kN/m3，黏聚力为24 kPa，内摩擦角为25 °。

表3-19　各土层土体参数

严格按照离心模型对应原型的几何尺寸，建立相应的Slide计算模型，采用Monte-Carlo方法抽样，样本数量为1 000，经验证，样本数量足够多，计算精度满足要求。选用简化Bishop法进行全局最小概率分析，计算结果如图3-74所示。水平软弱地基路堤虽具有对称性，但此处仅考虑其由右向左的滑动。可见，两组模型所获得的最危险滑动面均呈路堤连同地基一块滑动的圆弧状，滑动面虽深入至水平或斜坡软弱层，但未与下卧刚硬层相切，即未出现复式滑动。斜坡软弱地基路堤Slide模型所获滑动面形态与离心模型试验结果[图3-74（d）]基本吻合，这一定程度上证明了本章所建立的理论分析模型的可靠性，但水平软弱地基路堤离心模型并未发生失稳破坏[图3-74（b）]，下面不妨利用基于可靠度的原理阐述两组离心模型结果差异性的机理。

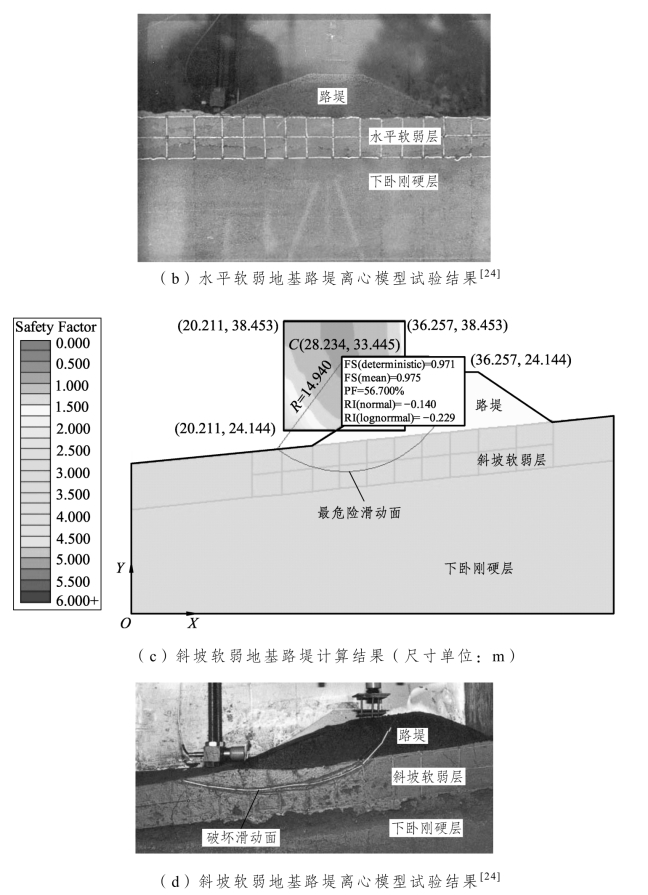
图3-74　Slide计算结果与离心模型试验结果对比

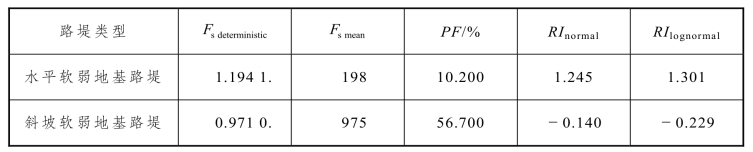
表3-20给出了利用简化Bishop法开展概率分析所获两组模型核心计算结果的对比。水平软弱地基路堤的确定性稳定安全系数、稳定安全系数的平均值均大于斜坡软弱地基，但数值基本上在临界值1左右波动。斜坡软弱地基路堤的确定性稳定安全系数比水平软弱地基路堤仅小18.7%，但破坏概率斜坡软弱地基路堤比水平软弱地基路堤高456%，同时可靠度指数水平软弱地基路堤也大于斜坡软弱地基路堤，这就充分证明了在其他条件不变的前提下，水平软弱地基路堤离心模型未发生失稳滑动，而斜坡软弱地基路堤发生了失稳滑动破坏。另外，尽管水平软弱地基路堤的稳定安全系数大于1，但仍存在10.200%的破坏概率，可靠度指数亦小于3，路堤仍有一定失稳滑动破坏的风险。即其他条件相同时，在斜坡软弱地基路堤确定性安全系数仅比水平软弱地基路堤略低的情况下，却存在高出水平软弱地基路堤甚多的破坏概率，自然更容易发生失稳滑动破坏。考虑路堤与斜坡软弱层土体材料变异性的可靠度分析方法比传统的确定性分析方法能更深刻地描述斜坡软弱地基路堤更易失稳的机理。

表3-20　两种路堤在简化Bishop法下的计算结果对比