斜坡软弱地基路堤力学行为及工程对策研究成果分享

2025-09-30 理论教育版权反馈

【摘要】：整体边坡方法所获整个斜坡软弱地基路堤的破坏概率PF为58.5%，比全局最小方法高0.7%，这说明整体边坡方法对斜坡软弱地基路堤的稳定性评价更趋于保守。

路堤、斜坡软弱层等土体材料及工程处治措施存在变异性，增加了斜坡软弱地基路堤的工程风险。随着现代计算机软硬件的发展，有必要将概率分析方法引入斜坡软弱地基路堤的稳定性分析课题中。Slide软件概率分析提供了全局最小（Global minimum）分析、整体边坡（Overall slope）分析两种方法。其中：全局最小概率分析方法假定按照确定性分析所获得的最危险滑动面发生滑动破坏的概率即为整个边坡的破坏概率，实际上当随机变量抽样不同时，滑动面不会仅局限于确定性分析所获得的最危险滑动面；整体边坡分析方法算法则相对更严谨。

为此，本节采用2D极限平衡法边坡稳定性分析软件Slide，在扼要比较全局最小与整体边坡两种方法原理的基础上，直接依据文献[24]所开展的斜坡软弱地基路堤离心模型试验成果，建立相应的极限平衡法模型，分析这两种概率边坡稳定性分析方法的优缺点以及适用条件，然后基于整体边坡方法，研究抗滑桩加固斜坡软弱地基路堤的稳定性，并与离心模型试验成果进行印证。

3.3.4.1　基于极限平衡法的两种概率边坡稳定性分析方法原理比较[46]

全局最小方法是先将各随机变量的均值代入模型开展一次确定性分析，得到一个最危险滑动面和一个确定性安全系数，假定最危险滑动面发生滑动破坏的概率即为整个边坡的破坏概率，使用样本数据针对此最危险滑动面计算安全系数，尔后计算破坏概率PF、可靠度指数RI等；而整体边坡方法则是用样本数据分别代入模型进行确定性分析，每份样本都可以计算得到一个最小的安全系数和一个潜在滑动面，这些潜在滑动面可能相同，也可能存有区别，其数量一般在10至50之间，破坏概率PF、可靠度指数RI等定义与全局最小方法相同，但其计算不再仅与某特定滑动面相关，而是包括了所有全局最小滑动面。

3.3.4.2　基于斜坡软弱地基路堤的概率边坡稳定性分析实例讨论

1.分析模型建立

如图3-63所示，严格按照文献[24]所开展的模型率为80的斜坡软弱地基路堤离心模型试验模型二所对应原型的几何尺寸建立Slide极限平衡法模型。其中，在路堤荷载作用影响范围内斜坡软弱层绘制网格，是为了更好地与离心模型试验结果开展对比。

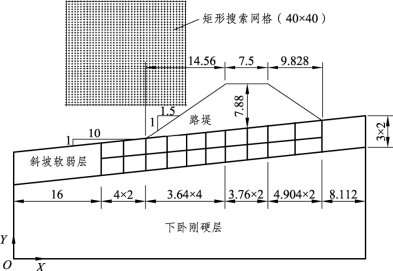
pagenumber_ebook=92,pagenumber_book=85

图3-63　斜坡软弱地基路堤Slide模型示意（未按比例，单位：m）

各土层材料均采用Mohr-Coulomb强度模型，只考虑路堤、斜坡软弱层土体材料的变异性，假定各土体参数变异服从正态分布。表3-13给出了反映路堤、斜坡软弱层土体材料变异性的计算参数，因现实生活中Mohr-Coulomb材料的黏聚力和内摩擦角通常相关联，即该材料拥有较低黏聚力时往往对应有较高内摩擦角，反之亦然[46]，故假定这两层土体的黏聚力和内摩擦角为负相关，相关系数均为－0.5。下卧刚硬层的重度为20.5 kN/m3，黏聚力为24 kPa，内摩擦角为25°。

表3-13　路堤与斜坡软弱层土体材料参数

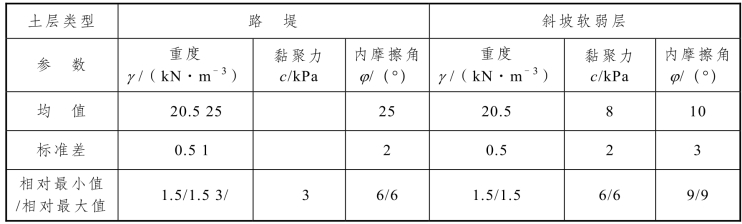
pagenumber_ebook=93,pagenumber_book=86

采用简化Bishop法，垂直条分所建模型。采用Monte-Carlo方法取样，经试算，样本数量取为1 000，即可保证计算精度。搜索方式为网格搜索，矩形搜索网格大小为40×40。

2.主要计算结果分析及讨论

全局最小与整体边坡两种可靠度分析方法计算得到的宏观结果如图3-64所示。由图可见，两种可靠度分析方法所获得的危险滑动面均呈贯穿路堤、斜坡软弱层的圆弧状，Slide模型所获危险滑动面与离心模型试验结果[图3-33（a）]基本吻合，这一定程度证明了本节所建立的Slide模型的可靠性。全局最小分析方法得到1个最危险滑动面［图3-64（a）］，整体边坡分析方法得到57个危险滑动面[图3-64（b）]，并大致组成2个滑动面群，从而描述了按照这些滑动面趋势发生滑动破坏的可能性。采用整体边坡方法还获得临界概率滑动面[图3-64（c）、（d）]、临界确定性滑动面[图3-64（b）]，注意到二者并不完全相同，临界概率滑动面半径略大于临界确定性滑动面。其中，临界概率滑动面一般拥有比整体边坡结果较高的可靠度指数和较低的破坏概率，而临界确定性滑动面表示当各随机变量取均值时，其安全系数Fs在所有潜在滑动面中最小，这个滑动面的破坏概率PF和可靠度指数RI与图3-64（a）所示采用全局最小方法所获破坏概率和可靠度指数相同。

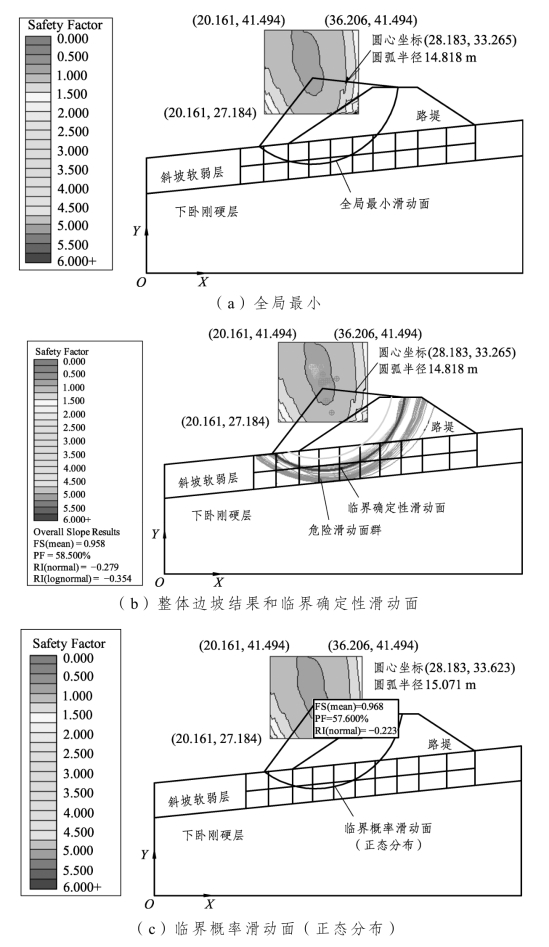
pagenumber_ebook=94,pagenumber_book=87

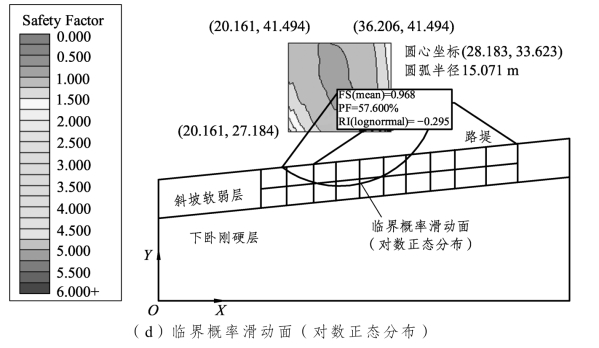
pagenumber_ebook=95,pagenumber_book=88

图3-64　全局最小和整体边坡计算结果对比

表3-14给出了两种可靠度计算方法破坏概率PF、可靠度指数RI等具体结果的对比。全局最小方法只有1组结果，整体边坡方法有3组结果。整体边坡方法所获整个斜坡软弱地基路堤的破坏概率PF为58.5%，比全局最小方法高0.7%，这说明整体边坡方法对斜坡软弱地基路堤的稳定性评价更趋于保守。两种分析方法得到的安全系数均值Fsmean都小于1，且可靠度指数RI都远小于3，表明斜坡软弱地基路堤稳定性差，要发生滑动破坏，这与离心模型试验结果一致。在整体边坡方法结果中，整体边坡结果的可靠度指数RI最小，其后依次是临界概率滑动面和临界确定性滑动面。同时，整体边坡的破坏概率PF最高。这就充分说明了整体边坡方法不再局限于单一滑动面，边坡破坏可沿任意滑动面发生，从而更真实、严密地描述了基于概率方法的边坡失稳破坏可能性。还需要特别说明的是，表3-14中全局最小结果与文献[17]表5所列斜坡软弱地基路堤结果略有细微差异，这是二者矩形搜索网格的设定位置有所出入导致的，但计算精度仍应在可接受范围之内。(https://www.chuimin.cn)

表3-14　两种可靠度分析方法计算结果对比

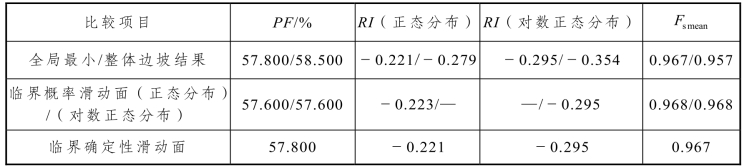
pagenumber_ebook=95,pagenumber_book=88

总的来说，整体边坡方法对斜坡软弱地基路堤稳定性的分析更全面。其计算结果使设计更趋于保守，同时得到了一组潜在滑动面，更好地展现了斜坡软弱地基路堤可能发生滑动破坏的宏观趋势。不过，整体边坡方法因各样本数据都要进行确定性分析，导致计算时间偏长。本模型计算时采用的计算机处理器是Inter（R）Core（TM）i5CPU、4GB内存（可用3.80 GB）、64位操作系统，采用全局最小、整体边坡方法计算机时分别为5 s、1 h 32 min15 s，后者是前者的1 107倍。

3.3.4.3　抗滑桩加固斜坡软弱地基路堤的整体边坡概率稳定性分析

1.分析模型建立

作为侧向约束措施，大截面的抗滑桩已成功应用于斜坡软弱地基路堤加固[2]，但通常采用传递系数法评价其稳定安全性[1]。正如前文所述，整体边坡方法得到的整个路堤的破坏概率PF高于全局最小方法，而抗滑桩加固工程成本高昂，不妨忽略整体边坡方法需耗费更多计算机时的弊端，采用整体边坡分析方法，以获得偏高的破坏概率，从而提高抗滑桩加固斜坡软弱地基路堤设计的可靠性。在前文所述模型基础上考虑抗滑桩加固，即距下坡脚5.3 m内侧处设置1排抗滑桩，其中桩长为20 m，纵向桩距为6 m。通过调整软件内嵌的微型桩的抗剪强度近似模拟抗滑桩，暂取每根抗滑桩的抗剪强度为4 000 kN。

采用Monte-Carlo方法抽样，经检验，样本数量为20 000时，统计分析收敛曲线末端已趋于平缓，表明样本数量足够多，精度满足要求。选用简化Bishop法进行整体边坡概率分析。假设抗滑桩抗剪强度和纵向桩距的变化均服从正态分布，其标准差、相对最小值、相对最大值分别为6 kN、18 kN、18 kN，0.1 m、0.3 m、0.3 m。土体材料计算分析参数仍如表3-13所列。同样假定这两层土体的黏聚力和内摩擦角相关系数均为－0.5。

2.主要计算结果分析及讨论

抗滑桩加固斜坡软弱地基路堤Slide整体边坡计算结果如图3-65所示。整体边坡方法得到15个圆弧状的危险滑动面。这些滑动面均穿过路堤和斜坡软弱层，未深入至下卧刚硬层，但滑动面范围明显大于无抗滑桩加固措施工况。如按照临界确定性滑动面发生滑动时，将滑面以上土体分为25个垂直土条，可计算得到抗滑桩将提供一个沿滑动面切线向上的大小为666.667 kN的抗剪力。

表3-15给出了抗滑桩加固后采用整体边坡、全局最小分析得到的计算结果的对比情况。可见，如采用整体边坡方法，其破坏概率PF比全局最小方法增加105.6%，可靠度指数RI和安全系数均值Fsmean均低于全局最小方法，这意味着同时考虑土体材料变异性和抗滑桩处治措施材质、施工等波动，采用整体边坡方法所获破坏概率明显高于全局最小方法。对比表3-14，则说明经抗滑桩加固，整体边坡方法所获路堤稳定安全系数均值Fsmean增加了55%，无抗滑桩加固的破坏概率PF是加固后的316倍多，抗滑桩加固后的破坏概率PF偏低，路堤发生滑动破坏的风险已降至极低的水平；可靠度指数RI基本接近3或者大于3，大致符合设计要求。而斜坡软弱地基路堤抗滑桩加固的离心模型试验（所对应的原型几何尺寸同图3-63，抗滑桩横截面尺寸为2.5 m×1.5 m，桩长20 m，纵向桩距6 m）结果[24]亦证明，抗滑桩加固后，斜坡软弱地基路堤变形较小，未发生滑动破坏（图3-66），这较好地印证了基于整体边坡分析所获结果的可信度。

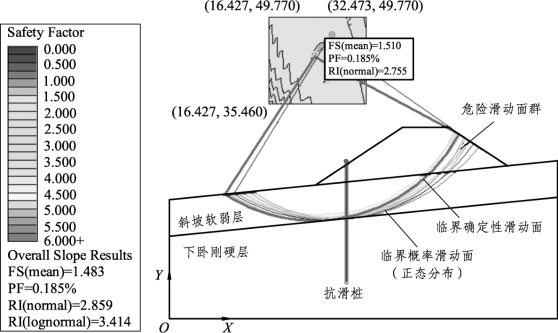
pagenumber_ebook=97,pagenumber_book=90