此处重点讨论软弱层竖向厚度d与沿路基纵向长度L改变时对斜坡软弱地基路堤稳定性的影响。图3-25FLAC3D分析模型图3-26给出了软弱层竖向厚度d为1 m，沿路基纵向长度L分别为20 m、100 m时FLAC3D计算获得的滑动面性态与2D强度折减法获得的滑动面性态的对比，其中2D强度折减分析计算采用加拿大的Phase2 V6.0进行。另外，鉴于水可软化路基，显著降低路基土的强度，在斜坡软弱地基路堤的设计施工中，应妥善处理好地表水、地下水等的防排水工作。......
2023-10-03
斜坡软弱地基路堤稳定性受拉裂缝影响的研究
【摘要】：3.3.2.1斜坡软弱地基路堤稳定性分析引入拉裂缝的必要性下面分别利用刚体极限平衡法、有限元剪切强度折减法建立斜坡软弱地基路堤稳定性分析模型，从推力线与滑体相对位置、相应土条受力及达到临界强度折减状态时的单元屈服分布几方面，论证斜坡软弱地基路堤稳定性分析引入拉裂缝的必要性。
开展黏性土坡稳定性分析时，可能观察到土坡上部出现拉力，通常因土体不能承受拉力而易导致此类分析欠严密，所以似有必要于黏性土坡稳定性分析中引入拉裂缝。一般情况下拉裂缝深度zc多采用Terzaghi [30]推导的基于半无限体朗肯土压力理论计算公式确定
式中：c、φ、γ 分别为土体的黏聚力（kPa）、内摩擦角（°）及重度（kN/m3）。
但此法仅适用于单一均质土坡。Spencer[31]假定土条条间力平行，根据推力线与滑面相对位置估算拉裂缝深度；Baker[32]引入数学变量极限求解方法，通过限定滑体几何和应力边界，在满足滑体力和力矩平衡的基础上，编制了拉裂缝深度求解程序，探讨了拉裂缝对边坡稳定性的影响；Taghavi[33]根据现场和试验测试数据拟合出一系列经验曲线，拉裂缝深度可由此查出。以上拉裂缝深度确定方法，未考虑拉裂缝深度的变化而直接求得其定值。在实际工程中，受多种因素影响，拉裂缝深度可能在一定范围内波动，进一步探讨拉裂缝深度的合理确定方法对提高黏性土坡稳定性分析精度具有重要意义。
我国西南地区斜坡软弱地基路堤广泛分布[34]，渝怀铁路斜坡软弱地基路堤土工离心模型试验表明该类路堤失稳时路堤顶面存在明显的裂缝[24]。本节应用加拿大Rocscience Inc.所开发的极限平衡法软件Slide、有限元法软件Phase2等，探讨在斜坡软弱地基路堤稳定性分析中引入拉裂缝的必要性，然后利用敏感性分析法确定拉裂缝分别在干燥和完全充水条件下的最不利深度，分析拉裂缝引入后对稳定安全系数、最危险滑动面形态及条间法向力的影响，阐述拉裂缝水分充填对稳定性的不利作用。
3.3.2.1 斜坡软弱地基路堤稳定性分析引入拉裂缝的必要性
下面分别利用刚体极限平衡法、有限元剪切强度折减法建立斜坡软弱地基路堤稳定性分析模型，从推力线与滑体相对位置、相应土条受力及达到临界强度折减状态时的单元屈服分布几方面，论证斜坡软弱地基路堤稳定性分析引入拉裂缝的必要性。
1.刚体极限平衡法模型
运用Slide软件，参考文献[24]所开展的土工离心模型试验所对应的原型几何尺寸，建立如图3-42所示的单线铁路斜坡软弱地基路堤极限平衡法分析模型。其中：路堤顶面宽7.5 m，路堤中心线填高7.88 m，路堤边坡坡比为1∶1.5；斜坡软弱层坡比为1∶10，厚6 m，其下为刚硬层；地下水位线假定位于斜坡软弱层中部，且平行于地面横坡。以水面法考虑地下水的影响，该法可直接通过地下水位的相对位置计算孔隙水压u，相应的计算公式为
式中：γw为水的重度，取为9.81 kN/m3；h为土条条块底部中点至地下水位的竖直距离；Hu为孔隙水压系数，因地下水位线倾斜，Hu采用由地下水位线倾角α自动确定的系数cos2α。
地下水位线以上、以下土体重度分别采用天然重度、饱和重度。
各土层材料均采用Mohr-Coulomb强度模型，相关材料如表3-9所列，其中用于后续Phase2有限元剪切强度折减法计算的弹性模量E和泊松比μ一并在此列出。分析采用Spencer法，并基于自动网格法搜索滑面，网格数量30×30（即水平向、垂直向均等分为30个小格），通过适当调整网格位置使最危险滑面圆心尽可能位于整个网格的中心，以确保计算精准可靠。滑面类型设置为失效方向从右往左的圆弧形，垂直条分土条数为25条。
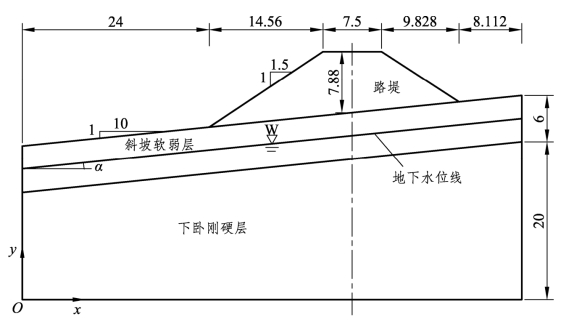
图3-42 斜坡软弱地基路堤分析模型（单位：m）
表3-9 各层土体材料参数
经计算，图3-43（a）给出了推力线与滑面的相对位置，可见推力线已超出滑体，这表明路堤上部已出现拉力。此时对应的稳定安全系数为0.933，已小于1.0，意味着斜坡软弱地基路堤已失稳。进一步检算土条条间法向力时发现，从坡脚至坡顶开始依次计数，从靠近后缘处的第22块土条开始，条间法向力均表现为负值，即出现受拉状态。其中，第22块土条受力如图3-43（b）所示，该土条的右侧条间法向力为－8.15 kN，这意味着路堤坡顶后缘处已出现了拉力。这将诱发土体产生一定深度的拉裂缝，因此有必要在极限平衡法稳定性分析中引入拉裂缝。
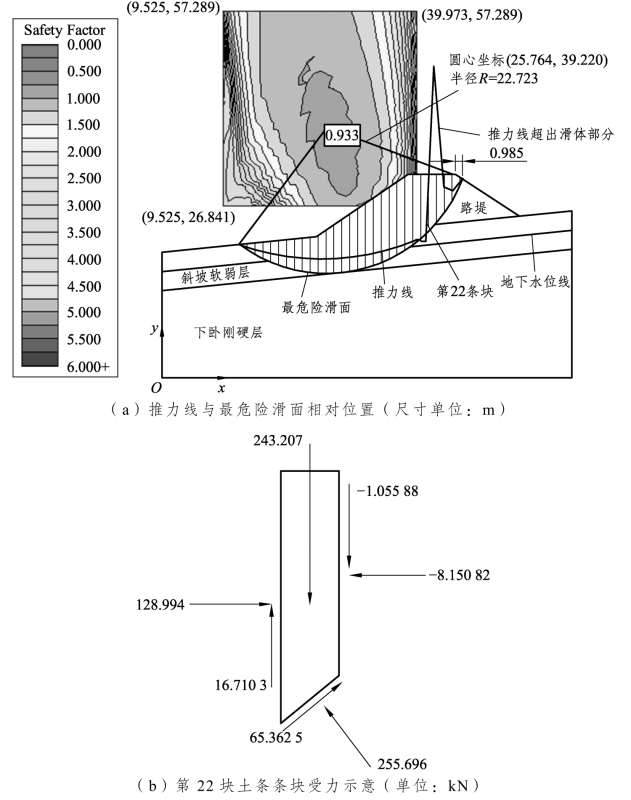
图3-43 极限平衡法分析所得结果
2.有限元剪切强度折减法模型
运用Phase2软件建立斜坡软弱地基路堤有限元剪切强度折减模型。模型的几何尺寸同图3-42，假定为平面应变问题，采用均匀三角形6节点单元离散模型，共划分 1 474个单元。暂不模拟路堤分层分步建造，只作为边坡问题考虑，初始应力以斜坡软弱地基路堤自重应力为准，模型的底侧、左右两侧均约束水平和竖直位移。材料为理想弹塑性、各向同性体，破坏准则采用Mohr-Coulomb模型，抗拉强度和剪胀角均设为0，材料参数参见表3-9。孔隙水压力计算方法同上述水面法。
经计算，图3-44（a）给出了用最大剪切应变云图表征的最危险滑面，滑面大致呈穿过路堤及斜坡软弱层的圆弧状，尚未出现复式滑动。图3-44（b）为强度折减系数与最大总位移的关系曲线，随着强度折减系数的增加，最大总位移增加，根据该曲线的拐点位置可知临界强度折减系数（即稳定安全系数）为0.92，此值略小于前文极限平衡法所获得的稳定安全系数。图3-44（c）为达到临界状态时单元拉伸屈服或剪切屈服的分布状况，其中圆圈表示拉伸屈服，叉表示剪切屈服，可见，路堤内大范围单元已处于拉伸屈服状态，这无疑从另一个角度说明在达到临界强度折减时斜坡软弱地基路堤上部已出现了拉力。
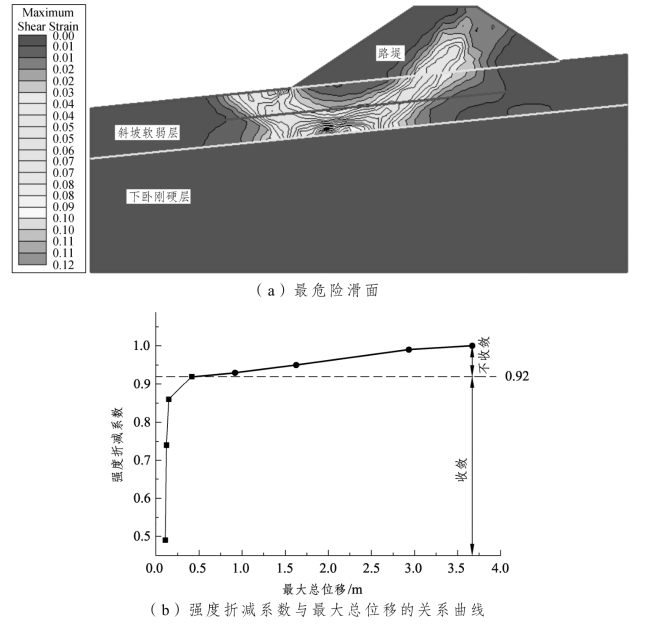
图3-44 有限元剪切强度折减法分析所得结果
3.3.2.2 基于极限平衡法敏感性分析的拉裂缝深度确定
1.利用敏感性分析法确定拉裂缝深度的基本思路
欲在极限平衡法稳定性分析中考虑拉裂缝的影响，拉裂缝深度的合理确定至关重要。在实际工程中，受多种因素的影响，拉裂缝深度可能在一定范围内波动，稳定安全系数随拉裂缝深度变化的趋势也可能并非单调。如能寻找到最小稳定安全系数所对应的拉裂缝深度，在此拉裂缝深度条件下的滑面形态无疑更真实客观。敏感性分析法较好地实现了这一意图。以Slide软件为例，该软件已成功内嵌敏感性分析法，利用其Sensitivity Analysis选项，可便捷地开展拉裂缝深度变化对边坡稳定性影响的敏感性分析。其基本算法是：分别设置最大、最小拉裂缝深度以确定拉裂缝深度分布区间，软件将拉裂缝深度区间均分为50份，分别计算50个不同拉裂缝深度所对应的全局最小稳定安全系数，绘制出稳定安全系数随拉裂缝深度变化的关系曲线；然后以稳定安全系数最小为原则，确定最不利的拉裂缝深度、最保守的边坡稳定安全系数和最真实的滑面。
2.基于斜坡软弱地基路堤的拉裂缝深度具体确定
根据Terzaghi的理论，一般情况下，拉裂缝最大深度不超过2zc[30]。将路堤的黏聚力、内摩擦角和天然重度代入前文所述Terzaghi拉裂缝深度计算公式，从而分别以路堤顶部、距离路堤顶部深度为7.658 m处为最小、最大拉裂缝深度，确定拉裂缝深度分布区间。为了探讨拉裂缝完全充水这一最不利工况下拉裂缝对路堤稳定性的影响，分别在拉裂缝干燥和完全充水条件下开展稳定安全系数随拉裂缝深度而变化的敏感性分析，计算得到稳定安全系数随拉裂缝深度变化的关系曲线，如图3-45所示。由此可见：当拉裂缝干燥时，稳定安全系数随拉裂缝深度的增加宏观呈现先减小后增大的趋势，稳定安全系数最小时所对应的最不利拉裂缝深度为4.22 m，拉裂缝深度为7.658 m时所对应的稳定安全系数小于拉裂缝深度为0 m时所对应的稳定安全系数；而当拉裂缝完全充水时，稳定安全系数随拉裂缝深度的增加宏观呈现递减趋势，稳定安全系数最小时所对应的最不利拉裂缝深度为7.658 m，该值远大于拉裂缝干燥时的工况。
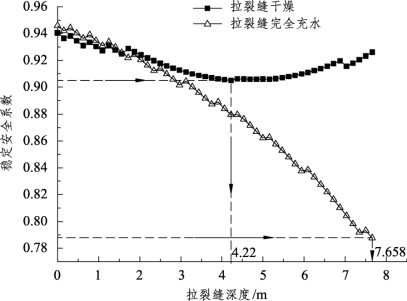
图3-45 稳定安全系数与拉裂缝深度关系曲线
3.3.2.3 拉裂缝对斜坡软弱地基路堤稳定性的影响
根据3.3.2.2节“2.基于斜坡软弱地基路堤的拉裂缝深度具体确定”的结果，分别在路堤上部设置深度为4.22 m的干燥拉裂缝和深度为7.658 m的完全充水拉裂缝，同时为对比分析相同拉裂缝深度条件下水分充填对路堤稳定性的影响，在深度为4.22 m的干燥拉裂缝深度基础上增补考虑水分完全充填的工况，分析对比这3种工况条件的稳定安全系数、最危险滑面形态及条间法向力的差异性。
1.稳定安全系数对比
图3-46给出了前文未考虑拉裂缝时所获稳定安全系数与后续3种工况下稳定安全系数的对比。可见，未考虑拉裂缝时极限平衡法（Spencer法）与有限元剪切强度折减法所得稳定安全系数略有出入，由于两者采用了不同的方法、原理、前提、假设等，后者比前者减小1.39%，后者设计更趋于保守；当考虑拉裂缝后，稳定安全系数均有所降低，其中相较于未考虑拉裂缝的极限平衡法，拉裂缝深4.22 m干燥、拉裂缝深4.22 m完全充水、拉裂缝深7.658 m完全充水工况的稳定安全系数分别降低了2.68%、6.22%、21.44%，这说明路堤稳定性分析中考虑拉裂缝将获得相对更低的稳定安全系数，使得设计趋于安全，但干燥拉裂缝对稳定安全系数削弱幅度不大。当考虑拉裂缝完全充水时，稳定安全系数急剧降低，需重点关注此时路堤的稳定性。如路堤顶部拉裂缝业已产生，应设法及时封堵以防止雨水进入。
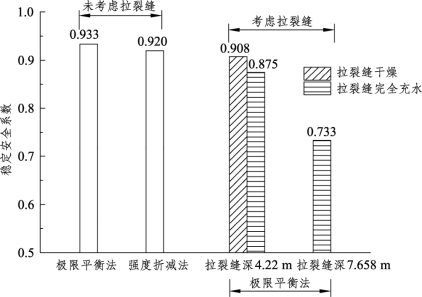
图3-46 各工况稳定安全系数比较
2.滑面形态对比
考虑拉裂缝后，3种工况路堤滑面形态如图3-47所示。可见，与未考虑拉裂缝时滑面呈圆弧状[图3-43（a）]不同，考虑拉裂缝后，滑面由靠近后缘路堤顶部的一段与拉裂缝深度等长的竖直线和一段圆弧共同组成，滑面起点（即拉裂缝位置）向路基左端靠近，滑体范围变小。在拉裂缝深4.22 m的情况下，拉裂缝充水程度的变化对滑面形态影响不大，与拉裂缝干燥条件相比，完全充水时滑面起点稍向路堤左端靠近，圆弧适当上移。当拉裂缝深度为7.658 m且完全充水时，滑面起点大幅度移向路堤左端，滑体范围急剧变小。尽管3种工况圆弧段圆心、半径不尽相同，但根据Spencer法所得到的推力线均位于由竖直线段与圆弧段所组成的滑面范围内，这说明考虑拉裂缝后路堤顶部的拉力已不复存在。
图3-47 3种工况所得滑面形态（尺寸单位：m）
3.条间法向力对比
图3-48给出了拉裂缝考虑前后土条条间法向力与距滑体前缘水平距离的关系曲线。由图可知，不考虑拉裂缝时，斜坡软弱地基路堤后缘坡顶处出现了负值条间法向力，即表明该处已出现了拉力，而在考虑拉裂缝之后，不管拉裂缝是干燥还是完全充水，土条条间法向力均为正值，拉力已消失。当拉裂缝深度增加后，距滑体前缘的水平距离依次减小，这一变化直接与图3-47所得滑面起点向路堤左端靠近、滑体范围变小的结论相吻合。此外，干燥拉裂缝最远距离处（即滑坡后缘最末端条块右侧）条间法向力为 0，而完全充水拉裂缝其值较大，这是受滑体后缘外部水压力作用的结果。根据Spencer法稳定安全系数计算公式，拉裂缝充填水分的影响将被视为坡面外力（此处为水压力），纵向单位宽度土体所受水压力计算公式为
式中：zw为所设拉裂缝填水深度。
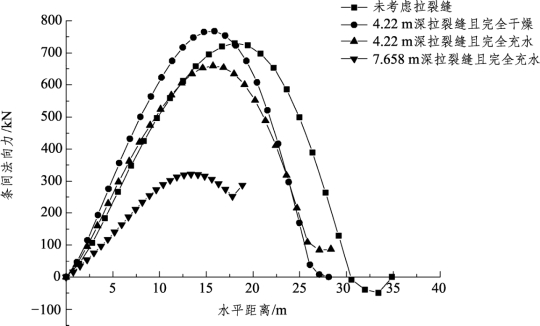
图3-48 土条条间法向力与距滑体前缘水平距离的关系
当拉裂缝深度为 7.658 m（软件实际计算取值为 7.657 7 m，此处为四舍五入）且完全充水时，计算所得水压力达到 287.631 kN，该水压力水平向左作用于距裂缝底部2.553 m（zw/3）处。巨大的水压力无疑加剧了下滑力，成为影响安全系数的关键因素。实际工程中对于已出现拉裂缝的边坡，宜及时就裂缝进行填浆勾缝封闭处理。
有关斜坡软弱地基路堤力学行为及工程对策研究的文章
- 详细阅读
-
斜坡软弱地基路堤抗变形能力研究详细阅读
复合地基可提高地基土体的强度，增强路堤连同地基的稳定性，有效减小地基侧向变形。旋喷桩法目前已在内昆铁路、遂渝铁路、渝怀铁路等斜坡软弱地基加固中获得成功应用。......
2023-10-03
-
斜坡软弱地基路堤变形及工程对策研究详细阅读
斜坡软弱地基路堤变形机理复杂，影响因素众多。相关人员对在不同的软弱层特性影响下斜坡软弱地基路堤的变形规律有何变化，不同的影响因素在变形中所占的权重如何等均缺乏统一认识，从而直接影响了工程措施的科学选择，极大地增加了工程风险及造价。......
2023-10-03
-
斜坡软弱地基路堤加固效果初探详细阅读
而经系梁式桩网结构加固后，随着路基的逐层填筑，其安全系数逐渐增大，当填筑至第5层后，安全系数较高且相对保持稳定。此过程中，最小安全系数为Fs＝1.644，显然满足Fs≥1.45的规范要求，系梁式桩网结构加固对提高斜坡软弱地基路堤安全性方面效果显著。相比无处治措施，经系梁式桩网结构加固处治后，其路基顶面的最大沉降、差异沉降分别减小约88.7%、90.3%，系梁式桩网结构可显著削减斜坡软弱地基路堤的沉降及差异沉降。......
2023-10-03
-
斜坡软弱地基路堤加固效果研究详细阅读
近年来，钢筋混凝土抗滑桩亦在斜坡软弱地基填方工程中获得应用，其基本做法是填方坡脚下沿纵向间隔排列抗滑桩，抗滑桩穿过表层斜坡软弱层与下卧刚硬层固结。张良等[26]对斜坡软弱地基路堤采用抗滑桩加固、打入桩加固等工况开展了土工离心模型试验，重点研究了路堤荷载作用范围内斜坡软弱地基的变形响应，但未关注抗滑桩内力分布、变位等力学响应。......
2023-10-03
-
斜坡软弱地基路堤变形耦合特性对比详细阅读
图4-28给出了4种地基条件下地基变形系数K随路堤分步建造而变化的关系。普通斜坡地基的地基变形系数K虽略微增加，但K值亦远小于1.0。水平软弱地基的地基变形系数K表现为先减小后增大，K值大小约为普通水平地基和普通斜坡地基的4倍，但低于斜坡软弱地基，且始终小于1.0，最大值仅为0.455。总体上看，地基变形系数K较小时，地基的侧向变形和竖向沉降绝对值不大。图4-284种地基条件下地基变形系数曲线......
2023-10-03
-
斜坡软弱地基路堤加固工作机理及对策研究详细阅读
以上的研究均仅单一地研究碎石桩或抗滑桩加固斜坡软弱地基路堤的机理，未涉及碎石桩与抗滑桩的联合加固，有可能碎石桩形成复合地基后再实施抗滑桩与天然地基直接实施抗滑桩两者的工作机理有所差异。......
2023-10-03
-
斜坡软弱地基路堤稳定性极限平衡法分析的研究成详细阅读
作为传统确定性稳定安全系数分析的有益补充，考虑以上各种变量随机性的可靠性分析应在斜坡软弱地基路堤稳定性极限平衡法研究中给予足够重视。......
2023-10-03
相关推荐