下面分别阐述一些主流强度折减法计算软件在进行边坡稳定分析时的主要特色。浙江大学开发的VFEAP程序亦可运用有限元强度折减法开展土坡稳定分析。......
2023-10-03
斜坡软弱地基路堤稳定性研究：二维剪切强度折减法
【摘要】：本节在文献[22]的基础上采用剪切强度折减法，重点从稳定性角度探讨斜坡软弱层性状对路堤的影响。故对于斜坡软弱层存在较严重尖灭度时，工程处治措施可参照“斜坡软弱层厚度对稳定性的影响”所述实施。图3-20软弱层尖灭度与安全系数的关系4.地面横坡对稳定性的影响假定地表斜坡软弱层厚度均匀且为2 m，图3-21给出了安全系数Fs随地面横坡的变化关系。
斜坡软弱层本身的性状，包括其厚度、在地基中的相对位置、是否存有尖灭度、地面横坡大小及软弱土体抗剪强度指标等，是斜坡软弱地基路堤设计与施工中必须要考虑的核心因素。本节在文献[22]的基础上采用剪切强度折减法，重点从稳定性角度探讨斜坡软弱层性状对路堤的影响。
3.2.2.1 计算原理及计算模型
稳定性分析采用FLAC3D内嵌的剪切强度折减法进行。该软件可通过命令“Solve fos”实现安全系数的计算：首先，通过给黏聚力设定一个大值来改变内部应力，以找到体系达到力平衡的典型时步Nr。然后，对于给定的安全系数Fs（Factor of safety），执行Nr时步。如果体系不平衡力与典型内力比率R<10－3，则认为体系达到力平衡；如果R﹥10-3，则再执行Nr时步，直至R<10－3后退出当前计算，开始新一轮折减计算过程[23]。
考虑到问题的平面应变性，故仅沿纵向取单位长度进行计算，以节约计算机时和硬盘存储空间。同时鉴于计算结果的精度依赖于网格的密度，所以需进行网格密度对计算精度敏感程度的相应调试，综合评价计算精度和计算耗时，从而确定合理的网格密度。
建立如图3-15所示的计算分析模型，其中路堤顶面宽度为7.5 m（单线Ⅰ级铁路），高度为8 m（以路堤中心线标高为准），路堤边坡坡比为1∶1.5，地面横坡为1∶n，用参数dl、dr分别表示模型左右两侧软弱层的厚度，并定义Δd=dl－dr为斜坡软弱层的尖灭度。如果Δd为负数，则表示表层斜坡软弱层左薄右厚；如果Δd为正值，则反之；当Δd=0时，则意味着软弱层厚度均匀，不存在尖灭度，此时用h表示软弱层厚度。
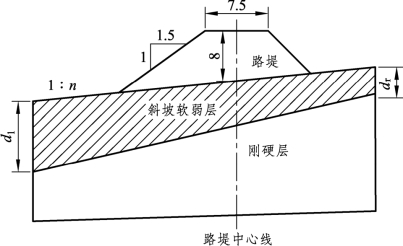
图3-15 斜坡软弱地基路堤几何计算分析模型示意（单位：m）
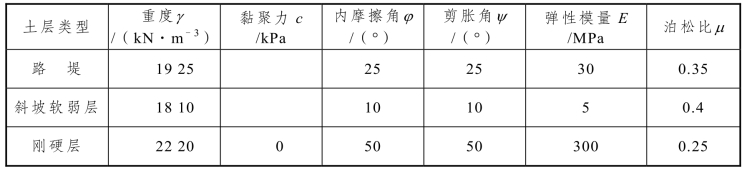
土体的本构模型均采用Mohr-Coulomb模型，抗拉强度设置为0，并采用相关联的流动法则，即视剪胀角与内摩擦角相同。参考文献[24]，各层土体参数的选取如表3-6所列。在FLAC3D软件中，不能直接输入弹性模量E和泊松比μ，需将其转换为体积模量K和剪切模量G输入。
表3-6 计算模型土体材料参数
3.2.2.2 参数敏感性分析
1.斜坡软弱层厚度对稳定性的影响
假定地表斜坡软弱层厚度均匀（即Δd＝0），图3-16给出了安全系数Fs随斜坡软弱层厚度而变化的趋势。由图可见，随着斜坡软弱层厚度h的增加，安全系数Fs呈曲线趋势降低，且初期降低十分迅速，后期趋于相对平缓。图3-17给出了斜坡软弱层厚度h为0 m、2 m、4 m、6 m、8 m、10 m时潜在滑移面形态的演变过程。当斜坡软弱层厚度为0 m（即问题转化为普通斜坡地基）时，潜在滑移面形态为通过坡脚的类圆弧状，且仅为路堤本体滑动，安全系数Fs为2.29；当斜坡软弱层厚度为2 m时，潜在滑移面呈现出复式形态，路堤本体内仍为圆弧，斜坡软弱层内滑移面则与刚硬层顶部相切，安全系数Fs为1.22；当斜坡软弱层厚度达到6 m后，潜在滑移面再次呈现为类圆弧状，路堤和斜坡软弱层均出现了滑动，滑动范围明显大于普通斜坡地基情况，但此时的潜在滑移面并未深入到斜坡软弱层底部，安全系数Fs为1.09。由此可见，实际地勘中如果遇到斜坡软弱地基，即使斜坡软弱层很薄，也应给予足够的重视。当斜坡软弱层的厚度大于4 m后，路堤安全系数Fs趋于平缓，斜坡软弱层厚度的继续增加对安全系数的影响不大。故当地表斜坡软弱层较薄时，不妨换填该层；地表斜坡软弱层较厚时，可于下坡脚一侧设置钢筋混凝土锚固桩，以有效降低侧向滑动趋势。锚固桩的桩长、锚固深度等可参考本节的理论分析成果而确定。
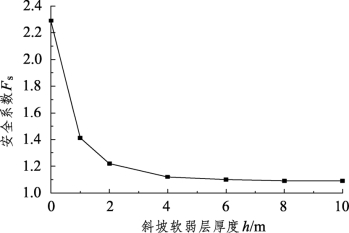
图3-16 地面软弱层厚度与安全系数的关系
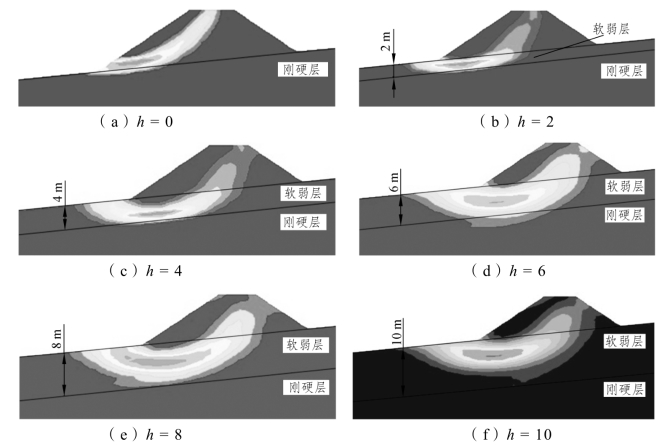
图3-17 软弱层厚度为h（m）时的潜在滑移面
2.斜坡软弱层在地基中相对位置对稳定性的影响
假定斜坡软弱层厚度均匀且为2 m，将其向下移动，以观察它在地基中的相对位置对安全系数的影响。图3-18给出了斜坡软弱层在地基中相对位置发生变化时，安全系数对应的变化关系。由图可知：斜坡软弱层相对位置较浅（0～1 m）时，安全系数Fs增大迅速；相对位置较深时，安全系数Fs趋于稳定。从潜在滑移面形态上看，斜坡软弱层相对位置较浅（0～1 m）时，潜在滑移面呈现为与下部刚硬层顶面相切的复式形态（图3-19）；相对位置较深时，滑移面形态与图3-17（a）类似，即为通过坡脚、仅路堤本体滑动的类圆弧状。这说明，对于实际工程，当斜坡软弱层在地基中位置相对较浅时，更需高度注意其失稳可能性，甚至可先挖除表面刚硬土层，进行必要软土处理后，再填筑路堤。当斜坡软弱层位于地表2 m以下时，安全系数已明显偏高，基本上可不对地基采取工程处治措施，而应加强路基本体的填筑质量控制，以防止路基本体的滑动。
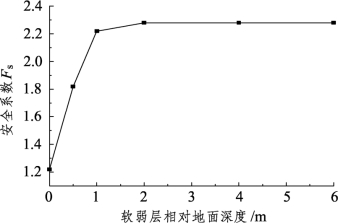
图3-18 软弱层相对位置与安全系数的关系
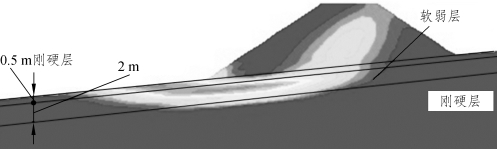
图3-19 软弱层距地面0.5 m时的潜在滑移面
3.斜坡软弱层尖灭度对稳定性的影响
斜坡软土的成因类型多属丘陵谷地相沉积，故常存在尖灭现象，即厚度的不均匀性。如前所述，本节将模型（参考图3-15）左右端软弱层厚度的差值dl－dr定义为尖灭度dΔ，且dr＝2 m，图3-20绘制了安全系数Fs随尖灭度Δd的变化趋势。可见尖灭度Δd值较小时，安全系数Fs降低迅速；随着Δd值的增大，安全系数Fs降低减缓，并趋于平稳。初期的潜在滑移面形态类似图3-17（b），呈现出与刚硬层顶部相切的复式形态；后期呈现出类似图3-17（e）所示的类圆弧滑动形态。这表明下坡脚软弱层较薄，上坡坡脚软弱层较厚的状况更容易引起失稳，需加倍重视此类地基的勘察工作；下坡脚一侧软弱层较厚（即尖灭度较大）时，相对于斜坡软弱层的尖灭度，斜坡软弱层厚度对路堤的稳定性占据了主要地位。故对于斜坡软弱层存在较严重尖灭度时，工程处治措施可参照“斜坡软弱层厚度对稳定性的影响”所述实施。
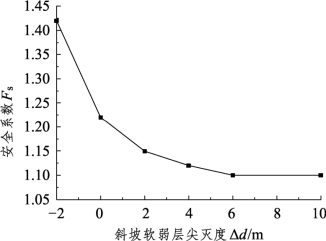
图3-20 软弱层尖灭度与安全系数的关系
4.地面横坡对稳定性的影响
假定地表斜坡软弱层厚度均匀且为2 m，图3-21给出了安全系数Fs随地面横坡的变化关系。由图可见，安全系数Fs随着地面横坡的增加呈现出近似线性的降低。当地面横坡为0（即为普通水平地基）时，潜在滑移面通过路堤及软弱层，呈对称的复式形态，见图3-22（a），安全系数Fs为1.42。存在地面横坡时，潜在的滑移面始终呈现出通过路堤本体和软弱层，且与刚硬层顶面相切的复式形态，潜在滑移面形态与图3-22（b）所示地面横坡为1∶5的情况类似，同时结合前文“斜坡软弱层厚度对稳定性的影响”“斜坡软弱层尖灭度对稳定性的影响”两节讨论，可知如果此时软弱层厚度增加，潜在滑动形态将逐渐变化为类圆弧状。当地面横坡为1∶5时，安全系数Fs为1.00，相对地面横坡为0的情况降低了29.6%。设计中，可利用安全系数随地面横坡的变化规律，确定在某一路堤高度、斜坡软弱层厚度条件下的安全系数下限，从而直接指导下坡脚一侧锚固桩桩长、锚固深度及桩位的确定。
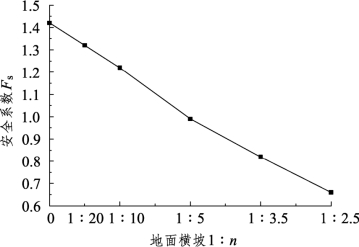
图3-21 地面横坡与安全系数的关系
图3-22 地面横坡变化时的潜在滑移面
5.斜坡软土抗剪强度指标对稳定性的影响
斜坡软土与刚硬土的主要区别之一就是土体的抗剪强度指标差异甚大，此处本书分别计算斜坡软土与刚硬土的黏聚力、内摩擦角之比cw/cs、φw/φs 对安全系数的影响，并统一将结果绘制成图3-23。由图可见：当斜坡软土与刚硬土的黏聚力之比值cw/cs小于0.4时，安全系数随比值增加而迅速增大；当比值大于0.4后，安全系数趋于稳定。随着斜坡软土与刚硬土的内摩擦角比值φw /φs的增加，安全系数的增大相对较缓，其变化规律类似抛物线。两者的比值达到1∶1后，对安全系数的影响相同，潜在滑移面的变化趋势都是从与刚硬层顶部相切的复式形态，发展成为通过坡脚仅路堤本体滑动的类圆弧状，见图3-17（a），滑移范围随抗剪强度指标的增大而减小。但前期两者之间的潜在滑弧位置存在差异，见图3-24（a）与（b），后期则趋于相似，见图3-24（c）与（d）。这种差异可从图3-23中反映出来，当斜坡软土的黏聚力和内摩擦角分别为0时，黏聚力为0的情况所得安全系数相对较高。故工程中应重视斜坡软土黏聚力和内摩擦角较小的情况，且提高软土的黏聚力相对能更迅速增强路堤的稳定性。
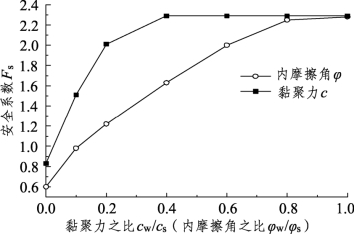
图3-23 斜坡软土抗剪强度与安全系数的关系
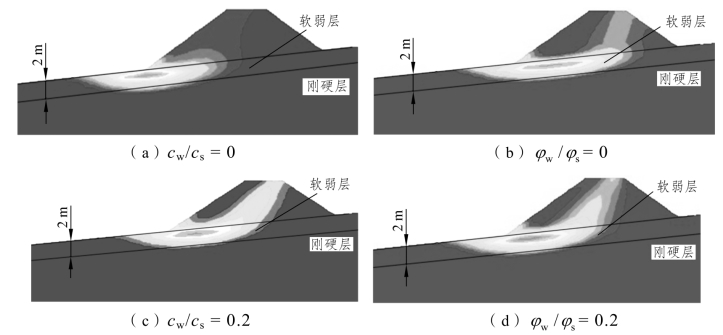
图3-24 斜坡软土抗剪强度变化时的潜在滑移面
有关斜坡软弱地基路堤力学行为及工程对策研究的文章
- 详细阅读
-
斜坡软弱地基路堤稳定性研究成果详细阅读
此处重点讨论软弱层竖向厚度d与沿路基纵向长度L改变时对斜坡软弱地基路堤稳定性的影响。图3-25FLAC3D分析模型图3-26给出了软弱层竖向厚度d为1 m，沿路基纵向长度L分别为20 m、100 m时FLAC3D计算获得的滑动面性态与2D强度折减法获得的滑动面性态的对比，其中2D强度折减分析计算采用加拿大的Phase2 V6.0进行。另外，鉴于水可软化路基，显著降低路基土的强度，在斜坡软弱地基路堤的设计施工中，应妥善处理好地表水、地下水等的防排水工作。......
2023-10-03
-
斜坡软弱地基路堤抗变形能力研究详细阅读
复合地基可提高地基土体的强度，增强路堤连同地基的稳定性，有效减小地基侧向变形。旋喷桩法目前已在内昆铁路、遂渝铁路、渝怀铁路等斜坡软弱地基加固中获得成功应用。......
2023-10-03
-
斜坡软弱地基路堤变形及工程对策研究详细阅读
斜坡软弱地基路堤变形机理复杂，影响因素众多。相关人员对在不同的软弱层特性影响下斜坡软弱地基路堤的变形规律有何变化，不同的影响因素在变形中所占的权重如何等均缺乏统一认识，从而直接影响了工程措施的科学选择，极大地增加了工程风险及造价。......
2023-10-03
-
斜坡软弱地基路堤加固效果初探详细阅读
而经系梁式桩网结构加固后，随着路基的逐层填筑，其安全系数逐渐增大，当填筑至第5层后，安全系数较高且相对保持稳定。此过程中，最小安全系数为Fs＝1.644，显然满足Fs≥1.45的规范要求，系梁式桩网结构加固对提高斜坡软弱地基路堤安全性方面效果显著。相比无处治措施，经系梁式桩网结构加固处治后，其路基顶面的最大沉降、差异沉降分别减小约88.7%、90.3%，系梁式桩网结构可显著削减斜坡软弱地基路堤的沉降及差异沉降。......
2023-10-03
-
斜坡软弱地基路堤加固效果研究详细阅读
近年来，钢筋混凝土抗滑桩亦在斜坡软弱地基填方工程中获得应用，其基本做法是填方坡脚下沿纵向间隔排列抗滑桩，抗滑桩穿过表层斜坡软弱层与下卧刚硬层固结。张良等[26]对斜坡软弱地基路堤采用抗滑桩加固、打入桩加固等工况开展了土工离心模型试验，重点研究了路堤荷载作用范围内斜坡软弱地基的变形响应，但未关注抗滑桩内力分布、变位等力学响应。......
2023-10-03
-
斜坡软弱地基路堤稳定性受拉裂缝影响的研究详细阅读
3.3.2.1斜坡软弱地基路堤稳定性分析引入拉裂缝的必要性下面分别利用刚体极限平衡法、有限元剪切强度折减法建立斜坡软弱地基路堤稳定性分析模型，从推力线与滑体相对位置、相应土条受力及达到临界强度折减状态时的单元屈服分布几方面，论证斜坡软弱地基路堤稳定性分析引入拉裂缝的必要性。......
2023-10-03
-
斜坡软弱地基路堤变形耦合特性对比详细阅读
图4-28给出了4种地基条件下地基变形系数K随路堤分步建造而变化的关系。普通斜坡地基的地基变形系数K虽略微增加，但K值亦远小于1.0。水平软弱地基的地基变形系数K表现为先减小后增大，K值大小约为普通水平地基和普通斜坡地基的4倍，但低于斜坡软弱地基，且始终小于1.0，最大值仅为0.455。总体上看，地基变形系数K较小时，地基的侧向变形和竖向沉降绝对值不大。图4-284种地基条件下地基变形系数曲线......
2023-10-03
相关推荐