剪切强度折减法vs软弱地基路堤力学行为与对策

3.2.1.1　剪切强度折减法软件特色简介

为适应复杂条件下边坡稳定性分析的迫切需求，国内外已相继开发出诸多已内嵌剪切强度折减法、可直接开展边坡稳定性分析的软件。下面分别阐述一些主流强度折减法计算软件在进行边坡稳定分析时的主要特色。

FLAC2D、FLAC3D是由美国Itasca Consulting Group Inc.开发的二维、三维有限差分法程序，可通过命令“Solve fos”实现强度折减算法，并通过剪切应变率云图和（或）速度矢量等来表征滑面的性态。后该公司进一步在FLAC2D的基础上，推出了FLAC/SLOPE。该程序可被视为FLAC2D程序的缩微版（Mini-version），专门用于边坡稳定的安全系数计算，完全基于FLAC2D的图形界面（Graphical Interface for Itasca Codes，GIIC），可轻松创建土质或岩质边坡模型并进行安全系数计算。这三个程序均采用支架法（Bracketing approach）自动搜索安全系数。

Plaxis是由荷兰Technical University of Delft开发的2D岩土工程有限元软件，强度折减法在该程序中被称为Phi/c-reduction。该程序可获得随着施工的逐步进行（如路基分步填筑），每一步的安全系数，不过材料必须为Mohr-Coulomb模式，并通过位移增量（Displacement increments）的云图、等值线或矢量图来表征潜在滑面的性态。我国清华大学宋二祥教授早年在荷兰留学工作期间曾参与了该程序在强度折减算法上的研发工作[18]，并提出了弧长控制法（Arc-length control），以使位移向量增量的内积在迭代过程中保持为常量为基本原则进行迭代，调整荷载增量的大小，从而得到可靠的极限状态及相应的强度参数值。目前，其较新版本V8.2中已可考虑强度折减时的更新网格（Updated mesh）和更新水压（Updated water pressure），从而实现大变形效应的精确模拟。后在Plaxis基础上开发的三维扩展包Plaxis 3D Tunnel、Plaxis 3D Foundation亦内嵌了强度折减法。

加拿大Rocscience Inc.开发的2D岩土工程专业有限元程序Phase2 V6.0，在运用剪切强度折减法分析边坡稳定性时，其材料模式可选用Mohr-Coulomb、Hoek-Brown（霍克-布朗）、Generalized Hoek-Brown（广义的霍克-布朗）及Drucker-Prager之一，并可设定剪切强度折减的区域，可由Slide（该公司开发的基于极限平衡法的边坡稳定分析程序）导入计算模型，甚至还可导入AutoCAD等的*.dxf图形交换文件，从而实现复杂边坡模型的快速建立，滑动面的性态可通过最大剪切应变（Maximum shear strain）的云图来表征，不过其缺陷在于不能如Plaxis一样，给出每步施工后的安全系数，而仅能给出最后一步的安全系数。

瑞士Zace Services Ltd.开发的ZSoil.PC程序也可进行类似剪切强度折减的边坡稳定性分析。

Geo FEM则是由FINE在原Geo 4基础上开发的。因采用c-phi折减与应力水平算法，Geo FEM与通常的滑动面方法相比显得更简便、通用。它使用六节点三角形单元离散土体，可使用Mohr-Coulomb、修正Mohr-Coulomb或Drucker-Prager等塑性模型，潜在滑动面可用等效塑性应变来描述。

韩国POSCO集团开发的MIDAS Family Program之一的MIDAS/GTS（Geotechnical &Tunnel analysis System，GTS）亦内嵌强度折减法，可进行复杂边坡的三维强度折减稳定性分析，通过最大剪切变形率的相关等值线来查看破坏形态。

在国内，东北大学开发的RFPA边坡版RFPA2D-SLOPE则内嵌离心加载法和强度折减法实现对边坡的稳定可靠性分析，在程序中输入工程实际参数，即可对边坡破坏过程进行模拟，在无须对滑移面进行搜索或者假定的情况下，即可得到边坡从滑移面的逐渐形成到最后的滑移破坏的全部过程。在对安全系数的计算中，该程序以基元破坏个数的最大值作为边坡失稳的判据。

浙江大学开发的VFEAP程序亦可运用有限元强度折减法开展土坡稳定分析。

万文等[19]（2004）则采用NCAP-FS程序进行数值分析，以系统达到临界平衡状态时所对应的材料参数降低倍数为整体最小安全系数。临界平衡状态定义为边坡内的塑性屈服区能够形成潜在的滑移通道时的状态。

3.2.1.2　算例分析与讨论

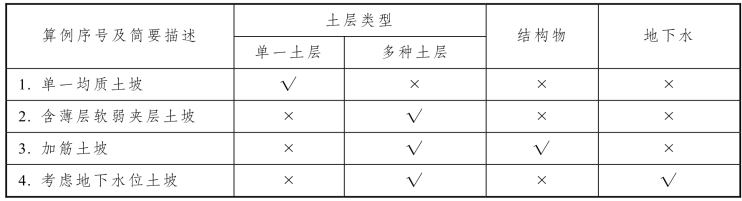
因FLAC/SLOPE与FLAC2D、FLAC3D，Plaxis与Plaxis 3D Tunnel在强度折减算法上的相同，且考虑到边坡工程多可视为平面应变问题，下面将以4个典型算例重点来比较FLAC/SLOPE、Phase2、Plaxis三个计算分析软件的一些特点。这4个算例分别为单一均质土坡、含薄层软弱夹层的土坡、加筋土坡及考虑地下水位土坡，4个算例的特点如表3-1所列。需要指出的是，以上算例均选自FLAC/SLOPE软件的手册[20]，该手册已给出了FLAC/SLOPE计算获得的成果。

表3-1　4个算例的特点

研究已表明，土体的弹性属性参数（弹性模量、泊松比）改变对安全系数的计算影响甚小。缺省状况下，FLAC/SLOPE程序将默认分析模型中所有材料的体积模量K＝100 MPa，剪切模量G＝30 MPa。为更好地对各软件进行横向比较，根据式（3-2），将K、G转化为弹性模量E、泊松比μ，分别为81.82 MPa、0.364，即在各程序中，均假定所有土层的弹性属性参数相同，均为E＝81.82 MPa、μ＝0.364（或K＝100 MPa、G＝30 MPa），同时假定重力加速度g均取10 m/s2、土体抗拉强度σt＝0、膨胀角ψ＝0，即采用非相关联的塑性流动法则。

1.单一均质土坡

图3-1为单一均质土坡计算分析模型示意。表3-2列出了其计算分析参数（其中，E为弹性模量，μ为泊松比，γ为重度，c为黏聚力，φ 为内摩擦角，下同）。其中FLAC/SLOPE计算分析时需填入密度ρ（可由重度γ 换算获得）、黏聚力 c、内摩擦角φ、膨胀角ψ 等参数，其他软件计算时还需要填入弹性模量E、泊松比μ，对于FLAC2D、FLAC3D程序，尚需按照式（3-2）将弹性模量E、泊松比μ 转化为体积模量K、剪切模量G，即需填入K＝100 MPa、G＝30 MPa。

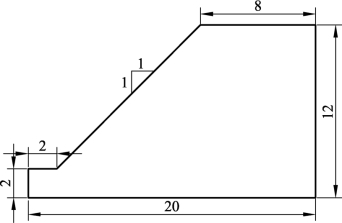
图3-1　单一均质土坡计算分析模型（单位：m）

表3-2　均质土坡计算分析参数

图3-2给出了不同计算软件所获得的滑动面的性态。需要指出的是，本书FLAC/SLOPE计算获得的安全系数为0.96，与手册[20]中的0.98略有出入，这是因为本书中土体的抗拉强度σt统一取为零，而不是手册中的1×1010Pa。从总体上看，三者获得的滑动面性态均为通过坡脚的类圆弧状，但Phase2的滑动面性态显然不如FLAC/SLOPE、Plaxis二软件更直观形象。实际上，当折减系数取较高值时，Phase2所表征的滑动面性态特征亦较明显。三者获得的安全系数非常接近（图3-3），Phase2获得的安全系数为0.99，略高于另二者，其偏差应在工程可接受范围之内。

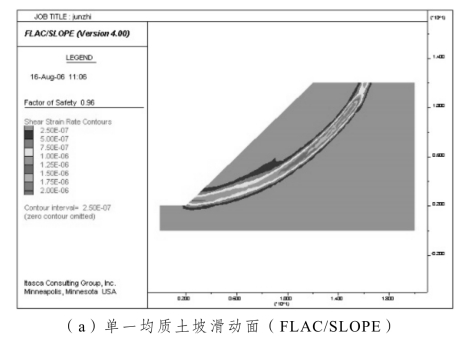
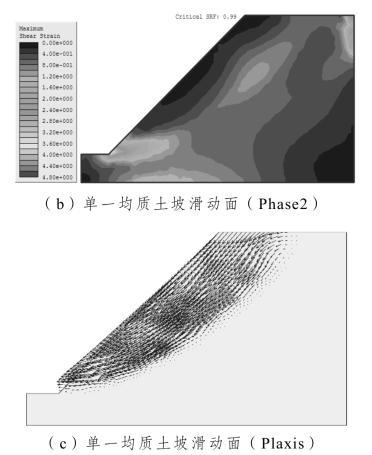
图3-2　不同软件下的单一均质土坡滑动面性态

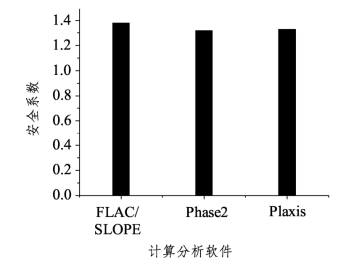
图3-3　单一均质土坡情况下不同软件计算所得安全系数比较

2.含薄层软弱夹层土坡

图3-4为含薄层软弱夹层土坡计算分析模型示意。表3-3列出了其计算分析参数。这样的土坡在运用传统极限平衡法分析时，常面临着如何判断复式滑面（Composite Slip Surface，CSS）出现可能性的难题。而运用强度折减法，则可较好地获得满意的解答。需要特别指出的是，Griffiths和Lane[21]（1999）曾对此问题进行过深入探讨。

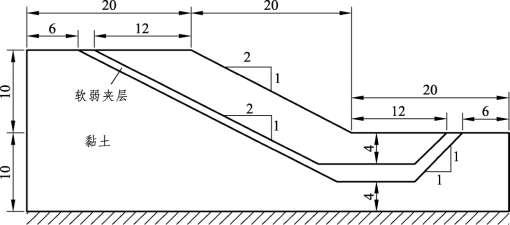
图3-4　含薄层软弱夹层土坡计算分析模型[20]（单位：m）

表3-3　含薄层软弱夹层土坡计算分析参数

图3-5给出了不同计算软件所获得的滑动面的性态。由该图可清晰看出，该土坡的滑动面大致有两条：一条表现为沿薄层软弱夹层的类直线滑动，一条则为大致通过模型底侧的类圆弧状滑动。这表明当软弱夹层与黏土黏聚力之比值逐渐增加的时候，潜在滑动面将由直线类滑动过渡到圆弧类滑动。本例中软弱夹层与黏土黏聚力之比值为0.6。同样，Phase2的滑动面性态仍不如FLAC/SLOPE、Plaxis二软件更直观形象。另需要引起注意的是，图3-2（c）是用位移增量的矢量图形来表征滑动面性态的，如用位移增量的等值线来表示Plaxis所获得的滑动面性态，则等值线密集处就是潜在滑动面的位置，如图3-5（c）所示。三者获得的安全系数同样接近（图3-6），FLAC/SLOPE获得的安全系数为1.38，略高于另二者。Phase2与Plaxis计算成果非常接近，其偏差应在工程可接受范围之内。

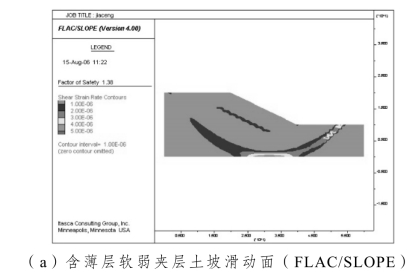
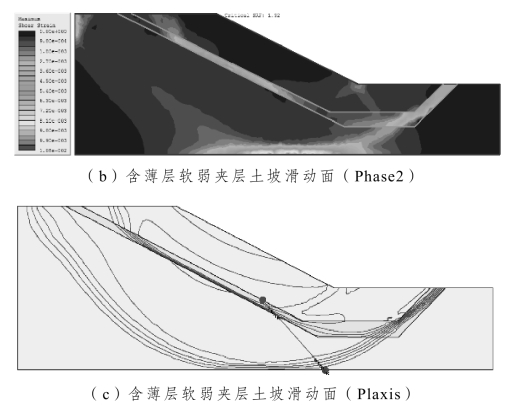
图3-5　不同软件下的含薄层软弱夹层土坡滑动面性态

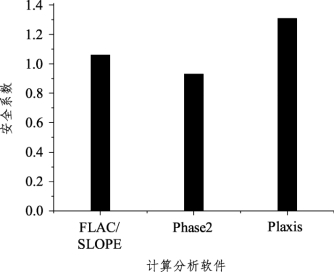
图3-6　含薄层软弱夹层土坡情况下不同软件计算所得安全系数比较

3.加筋土坡

图3-7为加筋土坡计算分析模型示意。表3-4列出了其计算分析参数。在以往的分析中，加筋土坡的稳定性分析多使用极限平衡法，视筋材的作用为等效拉力，而无法反映土-筋的相互作用，破坏模式是土体滑动、筋材拉断、土-筋界面破坏，还是沿土-筋界面滑移，这些问题如利用传统极限平衡法求解不易获得满意的答案。因各软件在处理筋材上所作的抽象、假设不同，不便于对筋材取完全相同的参数。在FLAC/SLOPE程序计算中，筋材的张拉屈服值为10 000 kN，黏结黏聚力为1 000 N/m，黏结摩擦角为30°，厚度为5 mm；在Phase2程序中，假定筋材的拉伸模量为10 000 kN/m，峰值拉伸强度为1 kN/m，回弹拉伸强度为0，筋-土界面无相对滑移；在Plaxis程序中，假定筋材为理想线弹性材料，轴向刚度EA＝10 000 kN/m，筋-土间亦无相互滑移。

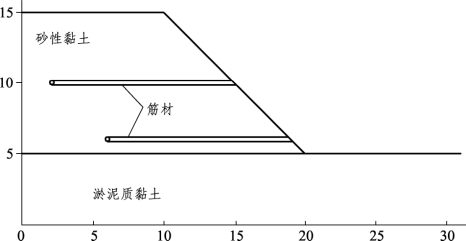
图3-7　加筋土坡计算分析模型[20]（图中坐标单位：m）

表3-4　加筋土坡计算分析参数

图3-8给出了不同计算软件所获得的滑动面的性态。仍需要指出的是，本书利用FLAC/SLOPE获得的安全系数为1.06，与手册[20]提供的解答1.08略有出入，是因为本书假定重力加速度g＝10 m/s2，且采用精细网格划分，而不是手册中的g＝9.81 m/s2及粗糙网格划分。由该图可看出，三者所获得的滑动面性态大体相似，筋材的铺设明显阻滞了土坡的滑动，滑动面的前端大致止于土体与最下一层筋材的交界处，这在图3-8（c）中表现得更为明显。

图3-8（a）同时绘制了筋材的轴力分布，由此可发现在滑动面所在位置处，筋材的轴力出现峰值，下层筋材靠路堤中心线侧亦有一个峰值，且上层筋材所受轴力大于下层筋材。但因三者在筋材处理上所做的假设、前提不尽相同，无法完全等效替换，故获得的安全系数差异较大，具体见图3-9。当然，这与是否考虑筋-土间发生相对滑移也有重要的关系。

图3-8（a）的筋材轴力分布也说明，上下两层筋材轴力的分布存在着差异，沿着筋材横向长度方向，轴力的分布既不是某恒定值，也不是某特定的分布函数，故在极限平衡法中简单地将筋材的作用等效为拉力（为恒值或某一特定分布函数）的做法显得较粗糙，欠科学。

图3-8　不同软件下的加筋土坡滑动面性态

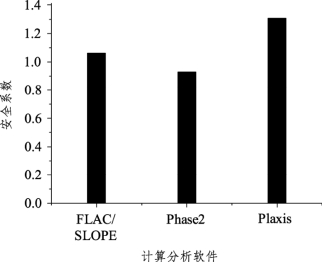
图3-9　加筋土坡情况下不同软件计算所得安全系数比较

4.考虑地下水位土坡

图3-10为考虑地下水位土坡的计算分析模型示意。表3-5列出了其计算分析参数。

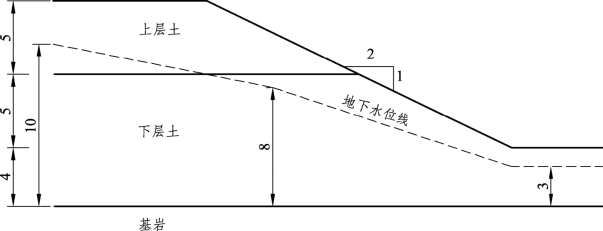
图3-10　考虑地下水位土坡的计算分析模型[20]（单位：m）

表3-5　考虑地下水位土坡的计算分析参数

图3-11给出了不同计算软件所获得的滑动面的性态。需要指出的是，本书用FLAC/SLOPE计算获得的安全系数为1.45，与手册[20]中的1.53有一定出入，这是由于本书假定重力加速度g＝10 m/s2，且采用精细网格划分，而不是手册中的g＝9.81 m/s2及粗糙网格划分。由该图可见，该土坡潜在滑动面表现为通过坡脚的类圆弧状，Phase2所展现的滑动面性态直观程度不如FLAC/SLOPE与Plaxis程序。三者获得的安全系数极为接近，如图3-12所示。

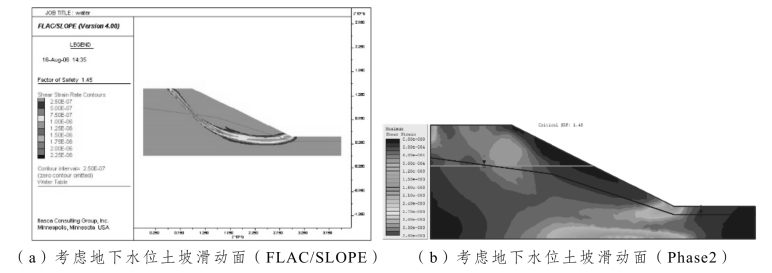
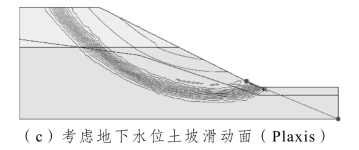
图3-11　不同的软件下考虑地下水位土坡滑动面性态

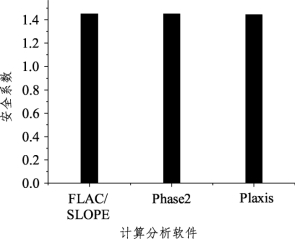
图3-12　考虑地下水位土坡情况下不同软件计算所得安全系数比较

图3-13绘制了利用Plaxis程序所获得坡趾节点的位移-总乘子增量的关系曲线，即关系曲线。注意到位移的大小并无意义，但它可表示是否已经发生破坏，即破坏时位移与安全系数关系曲线上表现为曲线基本水平，这是因为随着强度参数的减小，土体结构的相应位移会增大。土体趋于破坏状态时，在强度参数不变的情况下变形会持续发展，相应位移继续增大，而安全系数却不会再增大，因此曲线最终成水平状。

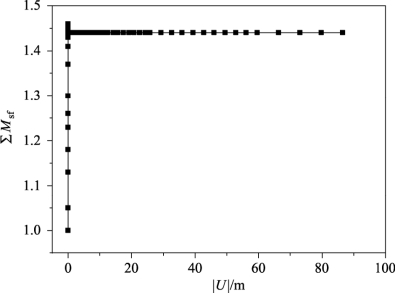
图3-13　安全系数评估曲线（Plaxis）

而在Phase2程序中，可绘制最大总位移与强度折减系数SRF（Strength Reduction Factor，SRF）的关系曲线，见图3-14。这意味着当强度折减系数小于临界强度折减系数1.45的时候，计算分析收敛；当大于临界强度折减系数后，最大总位移迅速急剧增大，计算即呈现发散状态。临界强度折减系数1.45就是所获得的安全系数。

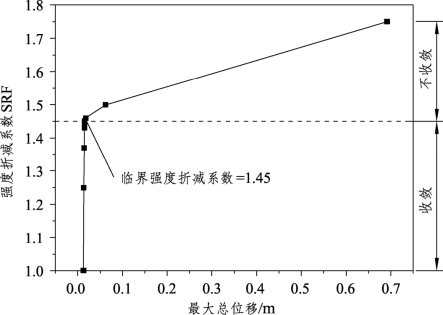
图3-14　强度折减系数SRF与最大总位移的关系曲线（Phase2）