T. Nagatani[6]提出了采用元胞自动机模型对交通事故引起的交通阻塞进行模拟，并探讨了在交通流模型中，交通事故的发生对动态阻塞相变的影响。钱勇生等[16]在 NaSh 模型的基础上，通过对交通事故和养护路段等意外事件对高速公路交通流的影响之研究，建立了意外事件影响的车道管制条件下的高速公路交通流元胞自动机模型，并通过数值模拟得出了意外事件的发生位置、堵塞时间和堵塞路段长度对交通流的影响。......
2023-09-26
蚁群算法原理及应用-城市道路交通事件影响分析与疏导策略
【摘要】：蚂蚁系统是蚁群算法最原始的模型，也被称为基本蚁群算法，它是之后所有蚁群算法的原型。蚁群算法最初是由Dorigo M 等提出并应用于解决经典的TSP 问题，并取得了极好的效果。因此，本书将引入TSP 问题系统介绍基本蚁群算法的数学模型。Nothegger[21]、Dowsland[22]等人将蚁群算法应用于求解多种不同类型的指派问题，例如二次指派问题、频率指配问题及图形着色问题等。
蚁群算法是一种模拟蚂蚁群体觅食行为的仿生类优化算法。此算法最早是由意大利学者Dorigo M等[16]在1991年提出的，并在之后的几年内对此算法的数学模型及核心思想进行了详尽系统的阐述。[17] [18]下面对该算法的数学模型及其应用进行简单的描述。
蚂蚁系统（Ant System）是蚁群算法最原始的模型，也被称为基本蚁群算法，它是之后所有蚁群算法的原型。蚁群算法最初是由Dorigo M 等提出并应用于解决经典的TSP 问题（traveling salesman problem），并取得了极好的效果。因此，本书将引入TSP 问题系统介绍基本蚁群算法的数学模型。
TSP 问题可以简单描述为：给定n 个城市，并已知各城市两两之间的距离，现有一旅行商需对每座城市进行一次访问并最终返回原地，要求找出一条总行程最短的巡回路径。此时，设 G = ( C , L)是一个有向图，其中
是n 个城市的集合，
是n 个城市两两连接的集合，dij 是lij 的长度，TSP 问题的求解目的即是找出长度最短的Hamilton 圈。
为便于描述基本蚁群算法求解上述问题的过程，首先对下文所需的参数变量进行说明：
b (t)表示t 时刻位于城市ci 的蚂蚁数；
m 表示蚁群中蚂蚁的总数，n 表示此问题中城市的总数，且
τij (t)表示t 时刻路段(i, j)上的信息素量，且设τij (0)为一个常量；
ηij 表示路段(i, j)的能见度，且
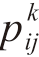(t)表示t 时刻蚂蚁k 由城市i 转移至城市j 的概率；
α 表示信息素的相对重要程度，反映了蚂蚁在选择路径的过程中信息素所起的作用；
β 表示能见度的相对重要程度，反映了蚂蚁在选择路径的过程中能见度所起的作用。
在初始时刻t = 0 时，各条路径的信息素τij (0)均相等，随机将m 只蚂蚁放置于n 个城市中，并采用禁忌表tabuk 记录蚂蚁k 当前走过的城市，依据一定的概率逐步选择下一个未访问过的城市。此处，t 时刻蚂蚁k 由城市i 转移至城市j 的概率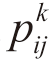
( t )主要由路段(i, j)上的信息素量τij (t)及能见度ηij 决定，其表达式描述如下：
式中，
表示蚂蚁k 下一步允许选择的城市集合。
当所有蚂蚁将所有城市都访问完成时，一个循环就结束了，此时为了避免出现遗留的信息素量过多而导致能见度信息被忽略，各路径上的信息素需进行更新处理。其更新规则表示如下：
式中， τ ij (t + n)为t+n 时刻路段(i, j)上的信息素量；∂为信息素的挥发系数，且∂∈(0,1)；Δτij ( t)为本次循环中路段(i, j)上的信息素增量；Δ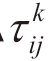 
(t )为蚂蚁k 在本次循环中释放在路段(i, j)上的信息素量。
针对不同的信息素更新策略，Dorigo M 分别提出了三种不同类型的基本蚁群算法模型：Ant-Cycle 模型、Ant-Quantity 模型、Ant-Density 模型，它们之间的区别主要在于Δτij ( t)计算方法的不同。
在Ant-Cycle 模型中，
式中，Q 为一只蚂蚁在本次循环中所释放的信息素总量，Lk 为蚂蚁k 在本次循环中所走路径的总长度。此模型是通过采用整体的路径信息，在完成一次循环后对所有路段上的信息素进行更新。
在Ant-Quantity 模型中，
此模型是通过采用局部的路径信息，在一个单位时间后对相应路径上的信息素进行更新，且其更新量与路径长度成反比。
在Ant-Density 模型中，
此模型同样是通过采用局部的路径信息，在一个单位时间后对相应路径上的信息素进行更新，但其只与单位时间释放的信息素量相关，与路径长度无关。
经对比研究发现，Ant-Cycle 模型相对于其他两种模型在TSP 问题的求解过程中具有更好的性能，因此通常将此模型作为基本蚁群算法。
由于该算法具有鲁棒性强、易于与其他算法相融合等优点，近年来其在指派问题、调度问题、车辆路径问题等许多应用领域均得到了极大的推广，且在算法的改进方面也获得了相关专家学者的广泛关注。
在应用方面，基于时间依赖理论、基于运货量及路径二维加载及带有时间窗等在内的多种条件，Gajpal[19]、Yu[20]等人采用蚁群算法求解了多种不同条件下的车辆路径问题。Nothegger[21]、Dowsland[22]等人将蚁群算法应用于求解多种不同类型的指派问题，例如二次指派问题、频率指配问题及图形着色问题等。除此之外，蚁群算法在多背包问题[23]、连续函数优化[24]、集覆盖[25]、机器学习[26]等方面的应用也均取得了极大的成功。在模型改进方面，Duan 等[27]通过对状态转移概率、信息素量、启发因子等因素进行自适应调节，达到对基本蚁群算法优化的目的。为了加快蚁群算法的求解速度，Yang 等[28]结合聚类分析理论将研究问题分解为多个子问题并求解，最终依据一定规则合成得出研究问题的最优解。蚁群算法具有易于陷入局部最优解的缺陷，Mishra 等[29]结合云模型对此缺陷进行了有效控制。
有关城市道路交通事件影响分析与疏导策略的文章
- 详细阅读
-
城市道路交通事件疏导策略及影响分析详细阅读
基于上述考虑，本书提出了结合蚁群算法及正交试验设计的动态交通网络配流模型，快速生成交通事件疏导配流方案，达到及时疏导、抑制拥堵的目的。因此，为了有效弥补上述两个主要缺陷，本书将通过采用正交试验设计的方法生成初始解，并改进信息素的更新方式及状态转移概率的确定方法，以实现对蚁群算法的优化。......
2023-09-26
-
城市道路交通事件影响及疏导策略分析详细阅读
G：路网T：时段k：时刻q：交通流量q j (k)：元胞j 在(k, k+1)时段的交通流量ρ：交通密度ρJ：阻塞密度ρo, j：元胞j 的临界密度值ρc：拥挤流向自由流转变的临界车流密度ρf：自由流向拥挤流转变的临界车流密度ρi (k)：第k 个时段元胞i 的车流密度ρiJ：元胞i 的阻塞密度v：自由流速度vli：元胞i 处的限速值vi (k)：第k 个时段元胞i 的平均车速v：控制区内元胞i......
2023-09-26
-
城市道路交通事件影响分析与疏导策略详细阅读
交通事件主要通过两种方式对交通流状态产生直接影响：其一，减少可用车道数；其二，导致驾驶人作出观望、减速、换道及更改出行路径等行为。调查发现，交通事件是引起交通拥堵的最重要的原因之一。因此，为了明确描述交通事件的影响，本书结合偶发性交通拥堵的特征，并基于疏导策略的需要，采用以下指标构建交通事件影响评价指标体系。......
2023-09-26
-
城市道路交通事件疏导策略与影响分析详细阅读
之后，Roberg[39]又利用仿真模型研究分析了在理想网络中以转弯禁限为主的交通事件疏导策略。之后，Sheu 等[45]又提出了一种基于实时交通事件响应匝道协调控制的随机最优控制方法，并借助微观交通仿真手段对各种模拟事件引起的拥塞情况进行了数值研究，相应的数值结果均表明该方法的可行性。......
2023-09-26
-
城市道路交通事件影响分析与疏导策略：处置区疏详细阅读
依据处置区的交通拥堵疏导策略，此区域内的路段主要应采取主线控制及入口匝道控制等措施。图6-5处置区示意图限速值的确定方法：若元胞i 处发生了一起交通事件，在此处则形成了一动态瓶颈，此时疏导的主要目的则是使尽可能多的车辆尽快通过此处瓶颈，以缓解车辆阻塞。......
2023-09-26
-
城市道路交通事件影响及疏导策略详细阅读
快速路交通事件的拥堵扩散特性相较于普通城市道路而言有较大不同，究其原因，这主要缘于其区别于普通城市道路的一些主要特征。因此，出入口处也成为快速路交通事件的高发区域，继而导致拥堵现象的频发。因此，快速路对其沿线的交通需求具有极大的吸引效应，尤其是对于一些以快速路为主要交通通道的城市则更甚。也正因为此，快速路上的交通事件相比于普通城市道路而言，往往会造成更大程度的影响。......
2023-09-26
-
城市道路交通事件影响范围与疏导策略详细阅读
事件影响范围可以直接反映交通事件发生后交通拥堵的扩散程度，它也是评价交通事件影响的最重要的指标。另外，为了具体描述交通事件引发的拥堵规模，将ILmax 定义为路段交通流恢复自由流状态前所能达到的最大事件影响长度，而该影响长度值对应的时刻即为最大影响时刻kmax。......
2023-09-26
相关推荐