传统的绕管式换热器的换热面积达9000～28000m2。绕管式换热器的制造方式各有不同,缠绕时要拉紧,并保证均匀。共有77540根管路,有2根管路因漏泄采用堵的方法,使换热器仍然正常运行。换热器的效率和压缩机的效率关系如下:式中,WLNG为液化所消耗的功;WR为制冷剂消耗的功;WC为压缩机的压缩功。WR是WLNG和所有换热器系统中不可逆损失之和,如温差、压降、控制阀和混合制冷剂的相互影响。......
2023-06-24
正交试验设计原理及应用
【摘要】：在1935 年的《试验设计法》一书中，费歇尔对“试验设计”进行了系统性的论述。[6]正交试验设计的过程主要可以分为以下三个步骤：依据试验目的，选定评价指标，并确定因素及其对应的水平。由于正交试验设计具有试验次数少、效率高、应用简单、效果显著等优点，使其在工农业等众多科学研究领域均得到了广泛的应用及推广。综上所述，可知正交试验设计是改进优化算法的一种有效手段。
1925 年，英国统计学家费歇尔在《研究工作中的统计方法》一书中，首次提出了“试验设计”的概念[3]，指出试验设计是以概率论、数理统计、线性代数为理论基础，科学地设计试验方案，正确合理地分析试验结果，以较少的试验工作量和较低的成本获取足够、可靠的有用信息。在1935 年的《试验设计法》一书中，费歇尔对“试验设计”进行了系统性的论述。[4]20 世纪40 年代，日本统计学家田口玄一在试验设计理论的基础上进行改进，首次提出了正交试验设计法的概念。它是使用正交表进行试验设计，来研究多因素多水平问题的一种数理统计方法[5]。通过此方法可以确定出各因素对试验指标的影响规律，以及各因素的主次影响排序与交互影响，并最终选择出一个各因素的水平组合使得指标值达到最优。[6]
正交试验设计的过程主要可以分为以下三个步骤：
（1）依据试验目的，选定评价指标，并确定因素及其对应的水平。
（2）选取适宜的正交表，确定试验方案，并获取试验结果。
（3）通过极差分析、方差分析等统计分析的手段，对试验结果进行解释分析。
在整个正交设计的过程中，其中最核心的要素即为正交表，它是利用均匀分散性与齐整可比性这两条正交性原理，从大量试验点中挑选适量的具有代表性、典型性的试验点，并按照一定规律所排列形成的规范化表格。其具体定义如下：设A 是一个n 行k 列的矩阵，其中第j 列因素由水平(1,2,…, m)构成，j=1,2,… ,k ，若A 的任意两列均衡搭配，则称A 是一张正交表。
正交表通常用符号
来表示，其中L 为正交表的代号；n为正交表的行数，表示试验方案的个数；k 为正交表的列数，表示试验因素的个数；mj 为第j 个因素所取的水平数，若某些因素的水平数相同，可以写成指数的形式。以正交表L8(2 7)为例，如表5-1 所示，该表包含了两水平的7 个因素，并由8 个试验方案组成，相比于使用全组合法，应有27 =128 个试验方案。因此，采用正交表极大地提高了试验效率。
表5-1 正交表L8 (27)
为了保证依据正交表设计出来的少量试验方案的合理性，任意正交表应满足以下两个性质：
（1）任意因素中各水平重复出现的次数均相等，且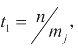
式中t1 表示第j 个因素中各水平出现的次数；
（2）任意两个因素所构成的各水平对重复出现的次数均相等，且
式中t2 表示第i 个因素与第j 个因素构成的各水平对出现的次数。
由于正交试验设计具有试验次数少、效率高、应用简单、效果显著等优点，使其在工农业等众多科学研究领域均得到了广泛的应用及推广。近年来，一些学者利用正交设计的优势，将其与某些优化算法进行融合，在收敛速度、参数确定等方面均获得了较大的改进。Gong、Wenyin 等人[7] [8] [9]采用正交设计法生成初始种群并设计交叉算子，对差分进化算法进行改进，提高了该算法的收敛速度。Zeng[10]、Cai[11]、Wang[12]等人将正交设计法与ε 占优、聚类分析等方法相结合，解决了多种多目标优化的问题。Ahmad[13]、Shi[14]、Li[15]等人通过引入正交设计，将遗传算法改进为正交遗传算法，极大地提高了遗传算法的局部搜索能力，并将其有效地应用于多种函数优化问题中。综上所述，可知正交试验设计是改进优化算法的一种有效手段。
有关城市道路交通事件影响分析与疏导策略的文章
- 详细阅读
-
正交试验得出复合酶最佳酶浓度比例详细阅读
根据8.2试验结果，以α-淀粉酶、半纤维素酶、纤维素酶、蛋白酶、果胶酶的浓度为因素，每个因素设计4个水平，以较能反应烟叶内在品质的施木克值作为指标，按正交表L16安排试验，因素水平表、试验方案和试验结果，如表8-1和表8-2所示。......
2023-10-28
-
撑杆设计及试验研究详细阅读
撑杆的设置在一定程度上减小钢箱梁的跨径，对于改善结构局部乃至整体的受力状态均比较有效。撑杆构件是改善该桥受力状态的关键构件，其处理方法没有经验可以参考。其在受压并承受一定水平剪力的同时，可能承受较大拉力。通过观测模型变形及应力分布，研究该撑杆的受力机理。通过试验，得到检测数据，对比验证理论分析的结果。图4-26撑杆加载试验......
2023-07-01
-
冻土试验仪器设备及工作原理详细阅读
箱内设置散热器、风扇、加热器、温度传感器，箱外设置制冷控温系统和二级温控器。散热器内设有循环液流通管，并与制冷控温系统相连，其控温原理与上述试样筒顶、底板的控温原理相同，只不过这里是散热器与箱内空气之间进行热交换。位移传感器布设在顶板上方，可测试试验过程中土样的轴向变形量。......
2023-10-02
-
FEKO仿真原理及应用详细阅读
定义参量在CADFEKO中左侧的树形浏览器中展开“Definitions”→“Variables”结点，双击“Variables”结点，在弹出的“Create variable”对话框中定义变量angle，初始值设为0。对话框中的“Yes”按钮，在EDITFEKO编辑器中进行如下操作。把如下脚本复制到IN函数的下边。修改后的EDITFEKO脚本如图6-67所示。图6-67 EDITFEKO脚本在EDITFEKO中，保存做过的修改，退出EDITFEKO。显示结果在CADFEKO的“Solve/Run”菜单中，单击“POSTFEKO”按钮，启动后处理模块POSTFEKO。......
2023-10-31
-
理解SVPWM调制原理及应用详细阅读
SVPWM的调制频率是三角波频率，三角波频率越高，电压谐波减小，这与SPWM调制是一样的，SVPWM是三角波与电压矢量时间系数K的比较，计算量较小，可以使系统响应更快。......
2023-06-19
-
电容器并联振荡回路试验的原理及过程详细阅读
振荡回路试验的原理是，把若干个电容器并联后，在较长时间内对脉冲电容器组充电，储存能量，然后经电感和被试断路器放电，产生一定频率的振荡电流，以在短时间内获得相当于短路电流的工频振荡电流供进行断路器开断能力试验。在被试断路器闭合状态时，接通QFh，形成振荡的放电过程，此时将被试断路器分闸，即可进行开断能力试验。单频振荡回路试验过程中的波形图如图5-11所示。......
2023-07-02
-
逆向创新的原理及应用详细阅读
逆向创新原理是从反面、从构成要素中对立的另一面分析，将通常思考问题的思路反转过来，有意识地按相反的视角去观察事物，寻找解决问题完全颠倒的新途径、新方法。逆向创新法也称反向探求法。当今世界上大量的新技术、新成果都是人们利用逆向创新原理不断探索创造出来的，是用传统思想方法所无法想象的。我国宋代司马光砸缸救小孩的故事，就是逆向思维方法，他不是将小孩拉出来而是用砸破水缸让水流走的办法，将小孩救出。......
2023-06-26
相关推荐