Kwon 与Varaiya[21]基于交通数据及交通事件发生的时间、地点数据，提出了一种高速公路交通事件影响算法，用以估计由交通事件引起的空间、时间影响范围及延误。结合拥堵状态下的实际数据，结果表明：所有的冲击波均独立于拥堵发生前的交通流速度。俞斌等[34]以交通波理论为基础，对路段和交叉口两种类型的交通事故每一段的交通波速度、排队长度进行了计算，最终确定其影响范围。......
2023-09-26
南京市道路交通事件影响范围预测模型参数标定
【摘要】：为了对普通城市道路交通事件影响范围预测模型的参数进行标定，本节选取了南京市主城区的局部路网作为研究对象，如图3-8 所示。依据所收集的数据，下面对包括自由流速度、非瓶颈路段通行能力、瓶颈路段通行能力、激波速度、阻塞密度在内的五个参数进行标定。因此，依据模型式，并通过数据拟合即可得出此研究路段的自由流速度值为55.3km/h。固定瓶颈路段的通行能力折减系数可以采用实测的历史数据，通过间隔统计模型标定得出。
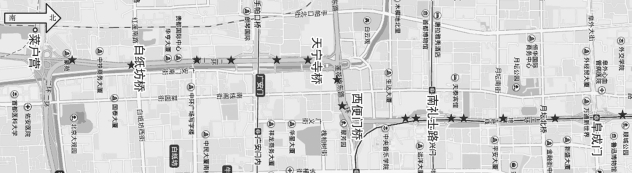
图4-5 研究路段示意图
为了实现对上文所构建模型的参数标定，并出于数据完整性、研究目标等方面的考虑，本书选取了北京市具有代表性的快速路特征路段作为研究对象。如图4-5 所示，此路段为西二环中由菜户营桥至阜成门桥之间的一段，全长为6508 米，行车方向为由南向北。图中星号所标示的为微波检测器所处的位置。
为了便于利用所建模型对交通事件的影响范围进行预测分析，可将此路段简化为一元胞划分示意图，如图4-6 所示。依据车道数、微波检测器及上下匝道所处的位置等因素，可将所选路段划分为20 个元胞，元胞内的数字即为元胞编号。元胞上最顶层的数字代表的是元胞内路段的车道数，元胞上底层的数字代表的是各个元胞的长度，单位为米（m）。元胞下的数字表示的是各个微波检测器的位置编号。元胞下各个箭头所处位置即为匝道所在位置，箭头朝下的为出口匝道，箭头朝上的为入口匝道。
在ECTM 模型中，元胞划分还需满足一个重要条件：元胞长度必须超过单位时间内处于自由流状态下的车辆的出行距离，即：
（时间步长设定为5s，自由流速度如下文所述进行标定）。若初步划分的元胞不满足上述条件，则需从这些元胞的下游元胞中适当划分部分路段分别归入各个元胞中，或是直接与其各自的相邻元胞合并。
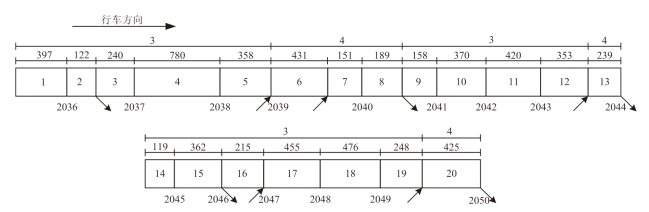
图4-6 元胞划分示意图
本书研究的数据主要来源于快速路上的微波车辆检测器（RTMS）所采集的数据及人工调查所获取的数据。其中，用于本研究的RTMS 数据主要包括各个监测器的流量、速度及占有率值，这些数据均为时间间隔是5min 的连续24h数据。另外，由于检测器故障等原因造成的数据缺失，则由人工调查的数据或历史数据来补充。依据所收集的数据，下面对包括自由流速度、非瓶颈路段通行能力、瓶颈路段通行能力、激波速度、阻塞密度在内的五个参数进行标定。
1.自由流速度
自由流速度是指交通密度趋于零时交通流的理论速度，即不受其他车辆干扰时的行驶速度。根据定义，本书利用研究路段某元胞一周内的RTMS 实测数据得出速度与密度的散点图，如图4-7 所示。从图中可以明显看出，速度与密度之间总体呈线性关系：当密度减小时，速度呈增长趋势。从图中可以看出，此关系曲线与Greenshields 模型比较吻合。因此，依据模型式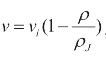
，并通过数据拟合即可得到当密度趋于0 时，研究路段内的速度值处于70km/h 至80km/h 的范围内。因此，本书研究路段的自由流速度的取值范围是70km/h 至80km/h。
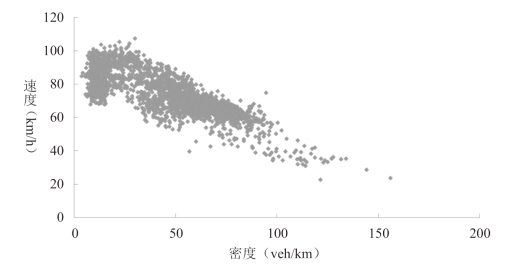
图4-7 研究路段速度-密度关系图
2.非瓶颈路段通行能力
非瓶颈路段的通行能力是指离开或进入某非瓶颈路段时所能达到的最大流量。但是由于这个流量值在实际情况下是很难达到的，因此如果直接将检测器的最大实测流量设置为此路段的通行能力是不合理的。此时，采用研究路段某元胞单车道一周内的RTMS 实测数据作出流量与速度的散点图，如图4-8 所示。从图中可以明显看出，速度与流量的关系曲线与经典的Greenshields 模型较为吻合。因此，依据模型式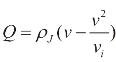
，当速度等于
时，流量（通行能力）可达到最大值。
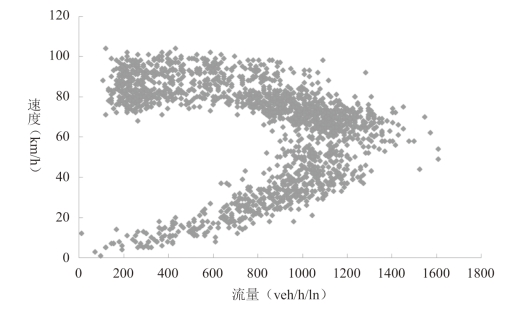
图4-8 研究路段单车道流量-速度关系图
由于研究路段内各元胞的通行能力不尽相同，因此通过实测数据拟合得出研究路段的单车道通行能力的取值范围为1700veh/h 至2200veh/h。另外，当实测数据发生缺失或错漏时，一般应选取大于2000veh/h 的通行能力值，以避免在仿真过程中出现一些不必要的瓶颈。
3.瓶颈路段通行能力
瓶颈路段是指容易引发交通堵塞传播或蔓延的路段。根据瓶颈路段产生原因的确定性与不确定性，可划分为固定交通瓶颈和动态交通瓶颈。固定交通瓶颈是指常发性拥堵的发生路段，因此具有一定的可预见性；而动态交通瓶颈则是指偶发性拥堵的发生路段，其主要是由交通事件突发、交通需求突增等不确定原因所引起的，具有较强的可变性，因此只在短时期内呈现一定的规律性。
由于瓶颈的产生，路段通行能力则需要进行一定程度的折减。固定瓶颈路段的通行能力折减系数可以采用实测的历史数据，通过间隔统计模型标定得出。动态瓶颈路段折减后的通行能力，其标定过程如下：以图4-9 为例，在元胞i 与元胞i+1 之间发生一起交通事件，产生动态瓶颈，导致上游元胞发生拥堵，而下游元胞仍处于自由流状态。此时，假定第k 时段内进入元胞i 的流量为
进入元胞i+1 的总流量为
（元胞i+1 折减后的通行能力），离开元胞i+1 的总流量为
而且从入口匝道驶入元胞i+1 的实测流量
小于元胞i+1 所能容纳的最大流量
。结合ECTM 模型，可将元胞i 和元胞i+1 的密度表达式分别描述如下：
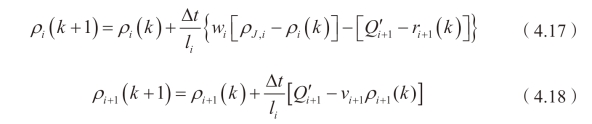
进入元胞i+1 的总流量
其中 y i+1( k)为第k 时段内从主路上元胞i 进入元胞i+1 的流量， ri +1( k)为第k 时段内从匝道i+1 进入元胞i+1 的流量。采用已有的yi+1 (k)与ri+1 (k)的实测值，可以通过下式对瓶颈路段通行能力Q′i+1 进行标定：
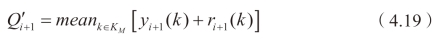
式中，KM 是指交通事件发生后至
的这段时间集合。其中，
是指函数y i+1( k )+ri +1( k )达到最大值时所对应的时刻。
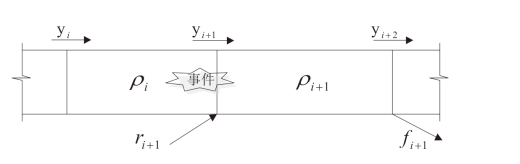
图4-9 动态瓶颈路段示意图
4.激波速度及阻塞密度
本书通过研究流量与密度之间的关系，采用约束最小二乘法对激波速度wi及阻塞密度ρJ, i 两个参数进行标定。首先，采用检测器实测的流量-速度值，通过下式得出元胞j 的临界密度值：
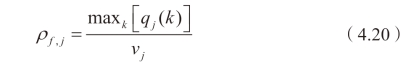
式中，qj (k)为元胞j 在(k, k+1)时段的实测流量。
由于在此标定过程中只需使用拥堵状态下的流量-密度数据组，因此本书将密度超过临界值
的数据组全部筛选出来作标定之用，并令其对应的k 值组成时间集KN，且 K N = {k 1 ,… ,kn}。同时，依据最小二乘法，令
作为下式的解：
式中，
上式中的Yj 与Xj 两个变量应呈线性关系，且应避免元胞j 的最大可能流量高于该元胞的通行能力Qj，即应受限于约束条件：
当某元胞估算出来的参数失真时，应选取相邻下游元胞的参数值来替代。通过以上方法进行估算得出研究路段的激波速度wi 的取值范围为20km/h 至25km/h，阻塞密度ρJ, i 的取值范围为88veh/km/ln 至105veh/km/ln。另外，由于发生交通事件而折减的激波速度及阻塞密度同样可以依据上述方法进行标定，不过应避免元胞j 折减后的最大可能流量高于折减后的通行能力Q′j，即受限于约束条件：
有关城市道路交通事件影响分析与疏导策略的文章
- 详细阅读
-
城市道路交通事件影响范围与疏导策略详细阅读
事件影响范围可以直接反映交通事件发生后交通拥堵的扩散程度，它也是评价交通事件影响的最重要的指标。另外，为了具体描述交通事件引发的拥堵规模，将ILmax 定义为路段交通流恢复自由流状态前所能达到的最大事件影响长度，而该影响长度值对应的时刻即为最大影响时刻kmax。......
2023-09-26
-
城市道路交通事件疏导策略及影响分析详细阅读
基于上述考虑，本书提出了结合蚁群算法及正交试验设计的动态交通网络配流模型，快速生成交通事件疏导配流方案，达到及时疏导、抑制拥堵的目的。因此，为了有效弥补上述两个主要缺陷，本书将通过采用正交试验设计的方法生成初始解，并改进信息素的更新方式及状态转移概率的确定方法，以实现对蚁群算法的优化。......
2023-09-26
-
交通事件影响范围的区域划分详细阅读
为了快速有效地实现疏导策略的总体目标，本书基于第四章所构建的快速路交通事件影响范围预测模型，根据不同的路网条件及车流密度值等指标，将预测所得的交通事件影响范围同样划分为以下三个处置区域：处置区、控制区及预警区，并依据不同的区域特征，确定各个区域的控制目标。通过细化总体控制目标，并针对各个子目标分别提出不同的疏导策略，以快速实现对交通事件拥堵扩散的有效控制。......
2023-09-26
-
城市道路交通事件影响分析及疏导策略详细阅读
T. Nagatani[6]提出了采用元胞自动机模型对交通事故引起的交通阻塞进行模拟，并探讨了在交通流模型中，交通事故的发生对动态阻塞相变的影响。钱勇生等[16]在 NaSh 模型的基础上，通过对交通事故和养护路段等意外事件对高速公路交通流的影响之研究，建立了意外事件影响的车道管制条件下的高速公路交通流元胞自动机模型，并通过数值模拟得出了意外事件的发生位置、堵塞时间和堵塞路段长度对交通流的影响。......
2023-09-26
-
城市道路交通事件影响及疏导策略分析详细阅读
G：路网T：时段k：时刻q：交通流量q j (k)：元胞j 在(k, k+1)时段的交通流量ρ：交通密度ρJ：阻塞密度ρo, j：元胞j 的临界密度值ρc：拥挤流向自由流转变的临界车流密度ρf：自由流向拥挤流转变的临界车流密度ρi (k)：第k 个时段元胞i 的车流密度ρiJ：元胞i 的阻塞密度v：自由流速度vli：元胞i 处的限速值vi (k)：第k 个时段元胞i 的平均车速v：控制区内元胞i......
2023-09-26
-
城市道路交通事件影响及疏导策略详细阅读
快速路交通事件的拥堵扩散特性相较于普通城市道路而言有较大不同，究其原因，这主要缘于其区别于普通城市道路的一些主要特征。因此，出入口处也成为快速路交通事件的高发区域，继而导致拥堵现象的频发。因此，快速路对其沿线的交通需求具有极大的吸引效应，尤其是对于一些以快速路为主要交通通道的城市则更甚。也正因为此，快速路上的交通事件相比于普通城市道路而言，往往会造成更大程度的影响。......
2023-09-26
-
钱塘江水质模型分析：影响预测结果的因素详细阅读
采用建立的水质模型，计算了12组方案的钱塘江河口水质，列出典型断面的COD Mn最大浓度见表4。表4各方案CODMn浓度模拟结果单位：mg/L由表4可知：上边界流量不同，水质有一些差别。小潮期富阳几乎不受潮汐影响，大潮期涨潮流明显，对污染物的稀释作用加强，水质明显优于小潮期；如对比表3中⑤和⑥，富阳河段水质可相差0.49mg/L，至里山相差0.11mg/L。由表3，取水流量不同对取水口集中的三江口—闸口段及其以上河段的COD Mn浓度影响不明显。......
2023-06-26
相关推荐