②车距控制信息由于处于预警区内的路段距离事发路段较远,可以利用的分流节点较多,对信息的诱导强度要求相对于处置区与控制区而言也较低。应通过处于白纸坊桥及广安门桥处的VMS 发布前方的拥堵路段,令前往拥堵路段方向的出行者提前作出适当选择。......
2023-09-26
在传统的CTM 模型中,交通事件对交通流的影响主要通过折减事发路段所在元胞的通行能力来反映,其折减系数则仅取决于事件影响下的阻塞车道数。然而,除了通行能力以外,事发元胞的其他主要交通流特征参数也会发生不可忽视的变化。因此,为了更加充分、真实地反映事发后元胞的交通流状态,本节将考虑包括通行能力、阻塞密度、临界密度及激波速度在内的多个主要特征参数的变化情况。另外,为了提高模型的准确性,本节将以实际采集的交通事件下的检测器数据为依据,对事发后的主要特征参数进行标定。
在所有受影响的交通流特征参数中,元胞通行能力是最能体现交通事件对交通流影响的参数。理论通行能力的降低可以通过交通事件导致的阻塞车道数计算得出,然而实际通行能力的降低却并非直接由阻塞车道数来决定的,它还受阻塞车道所处位置、阻塞车道车速、大型车比例、发生阻塞时驾驶人的观望情绪等因素的影响。早在20 世纪70 年代,Goolsby[29]便提出当交通事件造成三车道路段中的一条车道阻塞时,实际通行能力将降低50%;当造成其中的两条车道阻塞时,实际通行能力将降低79%。而Qin 和 Smith[30]采用美国弗吉尼亚州某条道路的实际采集数据,分析得出三车道路段中的一条车道或两条车道阻塞时,实际通行能力的降低比例达到63%和77%。
如上文所述,实际通行能力损失的比例显然超出交通事件影响下的阻塞车道数所占比例。因此,仅以阻塞车道数作为通行能力折减的依据是不够准确的。为了提高模型的准确性,本书将依据实际采集的交通事件下的检测器数据对交通事件影响下的元胞通行能力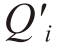 进行标定。具体方法如下:
进行标定。具体方法如下:
以图2-6 为例,假设在元胞i-1 与元胞i 之间发生一起交通事件,导致上游元胞发生拥堵,而下游元胞仍处于自由流状态。此时,假定第k 时段进入元胞i-1 的流量为![]() 进入元胞i 的总流量为
进入元胞i 的总流量为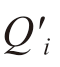 (元胞i 折减后的通行能力),离开元胞i 的总流量为vi ρi (k),而且从其他路径驶入元胞i的流量yi, r (k)均小于元胞i 所能容纳的最大流量Ri (k)。结合式2.13,可将元胞i-1 与元胞i 的密度表达式分别描述如下:
(元胞i 折减后的通行能力),离开元胞i 的总流量为vi ρi (k),而且从其他路径驶入元胞i的流量yi, r (k)均小于元胞i 所能容纳的最大流量Ri (k)。结合式2.13,可将元胞i-1 与元胞i 的密度表达式分别描述如下:
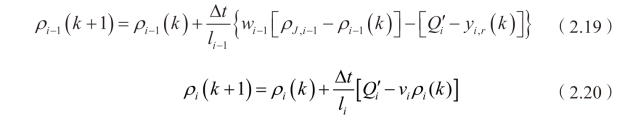
其中,进入元胞i 的总流量 ![]() ,其中yi (k)为第k 时段从当前路径元胞i-1 进入元胞i 的流量,yi, r (k)为第k 时段从其他路径进入元胞i 的流量。采用已有的yi (k)与yi, r (k)的实测值,可以通过下式对事发后的路段通行能力
,其中yi (k)为第k 时段从当前路径元胞i-1 进入元胞i 的流量,yi, r (k)为第k 时段从其他路径进入元胞i 的流量。采用已有的yi (k)与yi, r (k)的实测值,可以通过下式对事发后的路段通行能力 进行标定:
进行标定:
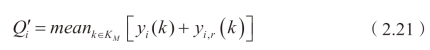
式中,KM 是指交通事件发生后至![]() 的这段时间集合。其中,
的这段时间集合。其中,![]() 是指函数 y i ( k )+ yi ,r ( k)达到最大值时所对应的时刻。
是指函数 y i ( k )+ yi ,r ( k)达到最大值时所对应的时刻。
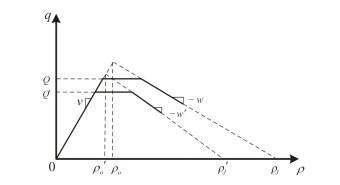
图2-7 受交通事件影响的流量-密度图
另外,由图2-7 中所示的基本图变化可知,随着交通事件的发生,除了通行能力之外,事发路段所在元胞的阻塞密度、临界密度、激波速度均会有一定程度的折减,由原本的ρJ, ρo, w 折减为ρ′J, ρ′o, w′。具体标定方法如下:
首先,结合检测器实测的流量数据,通过下式确定元胞i 折减后的临界密度值:

式中,qi (k)为元胞j 在(k, k+1)时段的实测流量。
然后,通过研究流量与密度之间的关系,采用约束最小二乘法对折减后的激波速度 及阻塞密度
及阻塞密度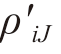 这两个参数进行标定。由于在此标定过程中只需使用拥堵状态下的流量-密度数据组,因此将密度超过临界值
这两个参数进行标定。由于在此标定过程中只需使用拥堵状态下的流量-密度数据组,因此将密度超过临界值![]() 的数据组全部筛选出来作标定之用,并令其对应的k 值构成时间集KN,且
的数据组全部筛选出来作标定之用,并令其对应的k 值构成时间集KN,且![]() 同时,依据最小二乘法,令
同时,依据最小二乘法,令![]() 作为下式的解:
作为下式的解:
![]()
式中,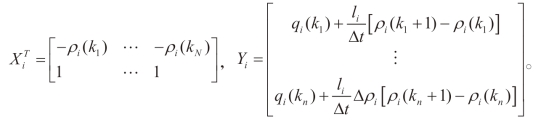
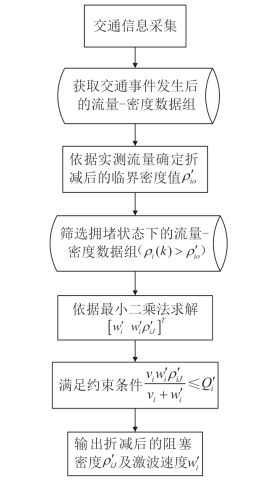
图2-8 交通事件影响下的交通流特征参数标定流程图
上式中的Yi 与Xi 两个变量应呈线性关系,且应避免元胞i 的最大可能流量高于该元胞折减后的通行能力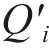 ′,即应受限于约束条件:
′,即应受限于约束条件:

依据上文描述,绘制的交通事件影响下阻塞密度、临界密度及激波速度的标定流程图如图2-8 所示。
有关城市道路交通事件影响分析与疏导策略的文章

②车距控制信息由于处于预警区内的路段距离事发路段较远,可以利用的分流节点较多,对信息的诱导强度要求相对于处置区与控制区而言也较低。应通过处于白纸坊桥及广安门桥处的VMS 发布前方的拥堵路段,令前往拥堵路段方向的出行者提前作出适当选择。......
2023-09-26

T. Nagatani[6]提出了采用元胞自动机模型对交通事故引起的交通阻塞进行模拟,并探讨了在交通流模型中,交通事故的发生对动态阻塞相变的影响。钱勇生等[16]在 NaSh 模型的基础上,通过对交通事故和养护路段等意外事件对高速公路交通流的影响之研究,建立了意外事件影响的车道管制条件下的高速公路交通流元胞自动机模型,并通过数值模拟得出了意外事件的发生位置、堵塞时间和堵塞路段长度对交通流的影响。......
2023-09-26

G:路网T:时段k:时刻q:交通流量q j (k):元胞j 在(k, k+1)时段的交通流量ρ:交通密度ρJ:阻塞密度ρo, j:元胞j 的临界密度值ρc:拥挤流向自由流转变的临界车流密度ρf:自由流向拥挤流转变的临界车流密度ρi (k):第k 个时段元胞i 的车流密度ρiJ:元胞i 的阻塞密度v:自由流速度vli:元胞i 处的限速值vi (k):第k 个时段元胞i 的平均车速v:控制区内元胞i......
2023-09-26

基于上述考虑,本书提出了结合蚁群算法及正交试验设计的动态交通网络配流模型,快速生成交通事件疏导配流方案,达到及时疏导、抑制拥堵的目的。因此,为了有效弥补上述两个主要缺陷,本书将通过采用正交试验设计的方法生成初始解,并改进信息素的更新方式及状态转移概率的确定方法,以实现对蚁群算法的优化。......
2023-09-26

依据处置区的交通拥堵疏导策略,此区域内的路段主要应采取主线控制及入口匝道控制等措施。图6-5处置区示意图限速值的确定方法:若元胞i 处发生了一起交通事件,在此处则形成了一动态瓶颈,此时疏导的主要目的则是使尽可能多的车辆尽快通过此处瓶颈,以缓解车辆阻塞。......
2023-09-26

事件影响范围可以直接反映交通事件发生后交通拥堵的扩散程度,它也是评价交通事件影响的最重要的指标。另外,为了具体描述交通事件引发的拥堵规模,将ILmax 定义为路段交通流恢复自由流状态前所能达到的最大事件影响长度,而该影响长度值对应的时刻即为最大影响时刻kmax。......
2023-09-26

本书的主要创新点可归纳如下:基于元胞传输模型,以交通流密度作为状态变量,针对交通事件发生的不同位置,调整了元胞的划分方式,将特征差异较大的事发路段与正常运行路段进行区别分析,重新确定了事件影响下各个元胞的发送函数及接受函数,并以实际采集的交通事件下的检测器数据为依据,构建了交通事件影响下的网络交通流模型,真实描述了事件发生后各路段的交通流状态,有效弥补了CTM 模型精度较低的固有缺陷。......
2023-09-26

快速路交通事件的拥堵扩散特性相较于普通城市道路而言有较大不同,究其原因,这主要缘于其区别于普通城市道路的一些主要特征。因此,出入口处也成为快速路交通事件的高发区域,继而导致拥堵现象的频发。因此,快速路对其沿线的交通需求具有极大的吸引效应,尤其是对于一些以快速路为主要交通通道的城市则更甚。也正因为此,快速路上的交通事件相比于普通城市道路而言,往往会造成更大程度的影响。......
2023-09-26
相关推荐