行程S在发动机设计中成为唯一的变数。气缸内径B与冲程S之间的比值,即Rsb的选择与发动机性能息息相关,因此在发动机设计因素中非常重要。这表示气门直径dV与侧压Fn在几何学上相互有关联。从图3-16中可以看出,行程越短,随Rsb传递到气缸、活塞的热量比率越大。因此,可以得出对于左右热传递的ψ值来说存在最佳的Rsb。这表示减少了同等量的冷却损失。......
2023-06-28
由于事发路段与其他路段的交通流特征差异较大,因此若能有效地将其分隔开,使其分属于不同的元胞,就能更加准确地描述出交通事件对道路交通的影响。为了实现此目的,模型首先应满足一个前提条件,即元胞长度的可变设计。然而,传统的CTM 模型是以元胞可容纳的车辆数ni (k)作为单一的状态变量,因此为满足元胞的流量守恒关系(如式2.2 所示),必须将元胞均匀划分,使其元胞长度均保持一致。由此可见,基于元胞长度的可变设计,是达成基于交通事件的模型改进的首要步骤。
为了达到此目的,本书选择以交通流密度作为状态变量,计算各时段元胞的驶入流量和驶出流量[27] [28],进而得到时段内各元胞的车流密度,通过对密度值的判断,以确定元胞内的车流状态。具体方法如下:
依据道路几何线形等道路条件将路段划分为若干元胞,如图2-6 所示。以元胞内的交通流密度作为状态参数,交通守恒模型可描述如下:
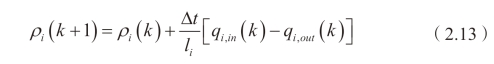
其中,ρi (k)表示第k 时段元胞i 的车流密度;li 表示元胞i 的长度,为避免出现元胞内车辆为负或车流密度大于堵塞密度的情况,元胞长度应不小于Δt内车流自由走行的距离;qi, in (k)与qi, out (k)则分别指(k, k+1)时段内单位时间所有进入与离开元胞i 的车辆数。
另外,由于此模型同样满足图2-1 所示的基本图,元胞i 的交通流状态则可由元胞密度ρi 与临界密度ρio 及阻塞密度ρiJ 进行对比判定得出:
若ρi <ρio,则元胞i 处于自由流状态;若ρio ≤ρi ≤0.5ρiJ,则元胞i 处于轻度拥堵状态,此状态下的交通流运行效率会受到轻度影响;若0.5ρiJ ≤ρi<0.7ρiJ,则元胞i 处于中度拥堵状态,此状态下的交通流运行效率会受到较大影响;若0.7ρiJ ≤ρi <ρiJ,则元胞i 处于重度拥堵状态,此状态下的交通流运行效率会受到显著影响,并易出现非完全阻塞状态下的排队现象;若ρi ≥ρiJ,则元胞i 处于阻塞排队状态。
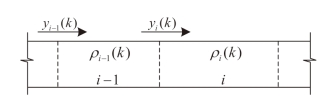
图2-6 元胞划分示意图
此时,此模型的路段模型的一般表达式描述如下:
第k 时段驶入元胞i 的车辆数可表示为:
![]()
式中,qi (k)为第k 时段元胞i 的流入率,第k 时段元胞i-1 的发送函数Si-1 (k)及第k 时段元胞i 的接受函数Ri (k)表示如下:

此模型的节点模型与CTM 的节点模型类似,同样也分为普通连接、合流连接、分流连接三种形式,具体计算公式如式2.4 至式2.12 所示。其中,第k时段驶入元胞i 的所有车辆数可表示为:
![]()
第k 时段驶出元胞i-1 的所有车辆数则可表示为:
![]()
有关城市道路交通事件影响分析与疏导策略的文章

行程S在发动机设计中成为唯一的变数。气缸内径B与冲程S之间的比值,即Rsb的选择与发动机性能息息相关,因此在发动机设计因素中非常重要。这表示气门直径dV与侧压Fn在几何学上相互有关联。从图3-16中可以看出,行程越短,随Rsb传递到气缸、活塞的热量比率越大。因此,可以得出对于左右热传递的ψ值来说存在最佳的Rsb。这表示减少了同等量的冷却损失。......
2023-06-28

喷嘴作为高速离心纺丝装置中的重要部件,其内部结构、直径和出口方向会影响射流的初始形状和纤维的运动轨迹,目前对于喷嘴结构的研究主要集中于喷嘴长度以及喷嘴直径对纳米纤维形态的影响。为探究喷嘴长度与喷嘴直径对PEO纳米纤维形态结构的影响,本实验以浓度为6%的纺丝溶液在4000 r/min转速下使用不同参数的喷嘴进行PEO纳米纤维的制备,进而观察纤维的直径分布。......
2023-06-23

本书的主要创新点可归纳如下:基于元胞传输模型,以交通流密度作为状态变量,针对交通事件发生的不同位置,调整了元胞的划分方式,将特征差异较大的事发路段与正常运行路段进行区别分析,重新确定了事件影响下各个元胞的发送函数及接受函数,并以实际采集的交通事件下的检测器数据为依据,构建了交通事件影响下的网络交通流模型,真实描述了事件发生后各路段的交通流状态,有效弥补了CTM 模型精度较低的固有缺陷。......
2023-09-26

桥梁的设计汽车荷载应根据表7.2-12选用,并应符合下列规定:快速路、次干路上如重型车辆行驶频繁时,设计汽车荷载应选用城—A级汽车荷载。......
2023-08-28

根据交通事件发生的不同位置,将元胞的划分方式调整如下:当事件发生位置恰好处于初始设置的元胞边界处时,此时初始的元胞划分无须发生改变。如图2-9 所示,当事件发生位置处于初始设置的元胞i 中间处,且元胞i 上游的事件影响段长度l′i <vi Δt 时,则将这部分路段与上游元胞i-1 重组为一个新的元胞i-1;同时,若原元胞i 下游的正常运行路段长度l′i <vi Δt 时,可将这部分路段与原下游元胞i+1 重组为一个新的元胞i。......
2023-09-26

7)确认当前图层为“图层1副本”。11)打开配套光盘中的“素材及效果\第6章 路径和矢量图形的使用\6.7.1画面设计\原图1.jpg”图像文件,如图6-77a所示。图6-82 创建放射状渐变图案图6-83 添加图层蒙版效果15)同理,利用配套光盘中的“素材及效果\第6章 路径和矢量图形的使用\6.7.1画面设计\原图2.jpg”图像文件制作出另外一张静物图的图层蒙版效果,效果如图6-84所示。......
2023-11-08

图4.4.20所示的模型是用可变截面扫描特征创建的异形壶,这是一个关于可变截面扫描特征的综合练习,下面介绍其操作过程。完成后,单击“完成”按钮;在操控板中单击按钮,预览所创建的特征;单击“完成”按钮。选择下拉菜单命令;选取图4.4.24所示的四条边线,圆角半径值为15.0。选择下拉菜单命令;要去除的面如图4.4.26所示,抽壳厚度值为8.0。......
2023-06-20

图5-12 所示为有限元模型,由弹体、PBX 装药、混凝土靶板组成,单元类型为三维实体单元SOLID164,利用六面体单元划分映射网格,靶板中心区域网格加密。软化曲线选择线性软化,该模型通过无量纲裂纹宽度ω 表征装药损伤情况,单元裂纹宽度l 与ω 的关系为表5-7PBX 装药的材料参数......
2023-06-27
相关推荐