基于特征参数ni的CTM路段模型及边界条件

2023-09-26 理论教育版权反馈

【摘要】：于是，以ni 为特征参数，可以将CTM 模型的流量守恒方程表述为：其中，yi 为时段元胞i-1 流入元胞i 的车辆数，并可由下式得出：其中，Qi 为在时段内流入元胞i 的最大车辆数，Ni 为k 时刻元胞i 所能承载的最大车辆数。图2-2CTM 模型的元胞划分示意图以上两式共同构成了CTM 路段模型的基本形式。而路段模型的边界条件则是由起始元胞的允许流入量及末端元胞的允许流出量来确定的。

CTM 模型的基本理论为：当交通流量q 与交通密度ρ 之间的关系满足图2-1 所示的基本图时，即可将宏观动力学模型（LWR 模型）离散化近似处理为元胞传输模型（CTM 模型）^[1] ^[2]：

式中，v 为自由流速度；w 为激波速度，即发生交通拥挤时车流向上游传播的速度；qM 为最大流量；qJ 为阻塞密度。

pagenumber_ebook=32,pagenumber_book=19

图2-1　流量-密度基本图

该模型将道路均匀划分成多个元胞（如图2-2 所示），元胞的长度等于自由流在一个时间步长Δt 内所运行的距离（一般选择100～1000m）。而k 时刻的交通系统状态则通过各个元胞中所包含的车辆数ni (k)来描述。于是，以ni (k)为特征参数，可以将CTM 模型的流量守恒方程表述为：

其中，yi (k)为(k, k+1)时段元胞i-1 流入元胞i 的车辆数，并可由下式得出：

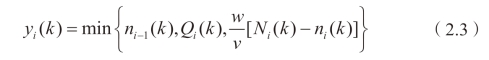
pagenumber_ebook=32,pagenumber_book=19

其中，Qi (k)为在(k, k+1)时段内流入元胞i 的最大车辆数，Ni (k)为k 时刻元胞i 所能承载的最大车辆数。

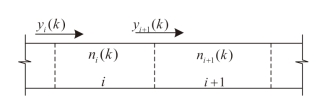
pagenumber_ebook=33,pagenumber_book=20

图2-2　CTM 模型的元胞划分示意图

以上两式共同构成了CTM 路段模型的基本形式。而路段模型的边界条件则是由起始元胞的允许流入量及末端元胞的允许流出量来确定的。为确定这两个值，可分别在起始元胞之前与末端元胞之后设置一个虚拟元胞，并令其具有无限大的尺寸，从而使得起始元胞传输的流量仅由其允许流入量决定，而末端元胞传输的流量也仅由其允许流出量决定。

基于特征参数ni的CTM路段模型及边界条件

相关推荐