两种性质完全不同的金属以及金属和非金属之间是很难焊接的，采用铆接或螺钉联接容易产生化学腐蚀和应力集中，而采用胶接常获得较好连接的效果。胶接接头为面面连接 应力分布均匀，应力集中较小，耐疲劳性能好。......
2023-06-26
圆的透视画法及应用场景
【摘要】：最后，作出圆管的轮廓素线，完成圆管的透视图。画圆的透视通常采用八点法，利用圆的外切正方形的四个切点以及对角线与圆的四个交点，先求出这八个点的透视，再用曲线板光滑连接成椭圆。图8—27所示为一位于基面上圆的透视作图。图8—30圆拱门的透视
1）当圆所在平面平行于画面时，其透视仍然是一个圆，只是因与画面距离不同而半径有变化。
图8—26所示是一轴线垂直于画面的水平圆管的透视。圆管的前端面位于画面上，其透视就是它本身，后端面在画面之后，与画面平行，其透视仍为圆，但半径缩小。为此，先求出后端面圆心C2的透视C°2，并求出后端面两同心圆的水平半径A2C2，B2C2的透视A°2C°2和B°2C°2，然后分别以此为半径画圆，可得到后端面的透视。最后，作出圆管的轮廓素线，完成圆管的透视图。
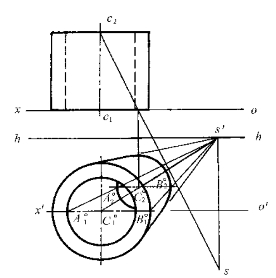
图8—26 圆管的透视
2）当圆所在平面不平行于画面时，圆的透视一般情况下为椭圆。画圆的透视通常采用八点法，利用圆的外切正方形的四个切点以及对角线与圆的四个交点，先求出这八个点的透视，再用曲线板光滑连接成椭圆。
图8—27所示为一位于基面上圆的透视作图。首先画出圆的外切正方形abcd，与圆相切于1，2，3，4点；然后连接对角线ac，bd，与圆交于5，6，7，8点。分别求出这八个点的透视，最后连成曲线即为圆的透视。作图时，用视线交点法作出正方形的透视a°b°c°d°，a°c°和b°d°的交点o°即为圆心的透视。至于5，6，7，8四点的透视，可延长F1o°，使与o′x′交于n，以n为圆心，以na°为半径画半圆，过n作45°直角三角形，在o′x′上得k，l，连F1k，F1l，与对角线a°c°，b°d°交于5°，6°，7°，8°四点，将1°，2°，3°，…，8°八点光滑相连，即得该圆的透视。
图8—27 八点法作水平圆周的透视
由上图可以看出，因受近大远小透视特性的影响，圆心o的透视o°并不是椭圆的中心。
图8—28所示为用上述方法画出的正圆柱体的透视。过a°取a°A°等于已知圆柱的高，然后过A°作顶圆的外切正方形ABCD的透视A°B°C°D°，顶圆和底圆上外切正方形的四个切点以及对角线与圆周的四个交点，其透视上下对应。最后根据母线的方向作出两条铅垂的轮廓素线，即得该圆柱体的透视。
凡是与基面平行的圆，均可采用上述方法画出其透视图。
当圆所在平面垂直于基面时，可采用图8—29所示的方法，画出其透视图。
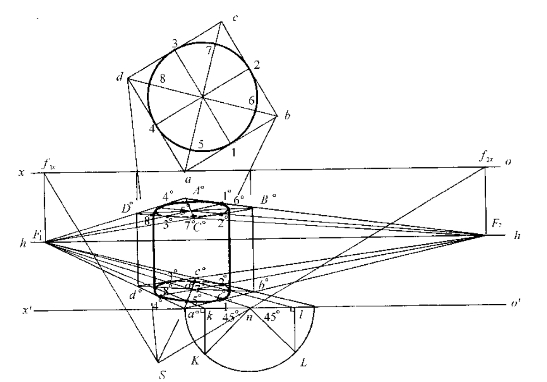
图8—28 正圆柱的透视
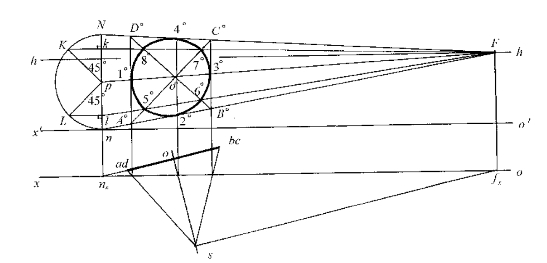
图8—29 八点法作铅垂圆周的透视
先作其外切正方形的透视A°B°C°D°，然后以真高线nN为直径画半圆，过圆心p作45°直角三角形，得k，l两点，连Fk，Fl，与对角线A°C°，B°D°交于5°，6°，7°，8°四点，连同外切正方形与圆周的四个切点的透视1°，2°，3°，4°共八个点，用曲线板光滑连接。
图8—30所示为圆拱门的透视作图，关键在于求作拱门前、后两个半圆弧的透视。作半圆弧的透视可完全采用图8—30的方法，将半圆弧纳入半个正方形中，作出半个正方形的透视，就可得到透视圆弧上1°，3°，5°三个点，再作出对角线与半圆弧交点的透视2°和4°，将这五个点光滑连接起来，就是前半个圆弧的透视。后半个圆弧的透视，可用相同方法画出。图中是利用过前后两个半圆弧上对应点连线的透视应指向共同灭点F2的特性，使作图简化。
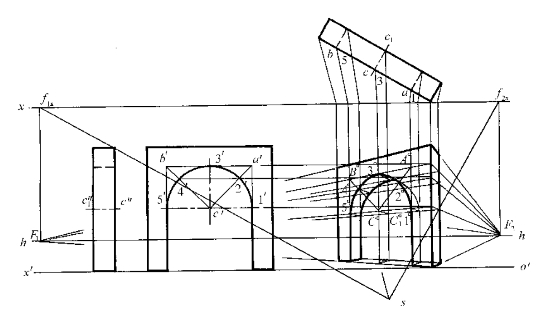
图8—30 圆拱门的透视
有关画法几何及土木工程制图（第4版）的文章
- 详细阅读
-
数控加工的特点及应用场景详细阅读
另外，数控加工工序相对集中，工艺复合化，使得数控加工的工序内容要求高，复杂程度高。数控加工过程是自动化进行，故还应特别注意避免刀具与夹具、工件的碰撞及干涉。......
2023-06-29
-
键联接的特点及应用场景详细阅读
紧键联接的特点是在键的上表面具有一定的斜度，装配时需将键打入轴与轴上零件的键槽内联接成一个整体，从而传递转矩。另外，当受到冲击、变载荷作用时，容易造成联接的松动。切向键联接能够传递很大的转矩，常用于对中要求不高的重型机械。花键联接一般用于定心精度要求高、载荷大或需要经常滑移的重要联接，在机床、汽车、拖拉机等机器中得到广泛应用。......
2023-06-25
-
磨床常见类型及应用场景详细阅读
平面磨床分为以下几种类型。磨削时，圆形电磁吸盘将工件吸在一起作单向匀速旋转，砂轮除高速旋转外，还在圆台外缘和中心之间作往复运动，以完成磨削进给。图13-1e所示为直线贯穿式双端面磨床，适用于磨削轴承环、垫圈和活塞环等工件的平面，生产效率极高。......
2023-06-28
-
视频信号的特点及应用场景详细阅读
例如，我们欣赏电视节目时，就是电视机将接收的电台信号，还原为图像信号的过程，那么该过程中视频信号就始终贯穿在“处理”的过程中，如亮度、色度信号处理电路等。图6-20 处理数字视频信号的电路及相关信号波形......
2023-06-26
-
模拟视频的特点及应用场景详细阅读
模拟视频是一种用于传输图像和声音的并且随时间连续变化的电信号。模拟视频具有以下特点：①以模拟电信号的形式来记录。传统的视频信号都是以模拟方式进行存储和传送的，然而模拟视频不适合网络传输，在传输效率方面先天不足，而且图像随时间和频道的衰减较大，不便于分类、检索和编辑。电视信号是视频处理的重要信息源。目前各国的电视制式不尽相同，不同制式之间的主要区别在于不同的刷新速度、颜色编码系统、传送频率等。......
2023-10-22
-
PARLED灯的特性及应用场景详细阅读
PAR灯是采用大功率LED作为光源并且需要专用的PAR灯透镜的灯具。包括PAR16、PAR20、PAR30、PAR38、PAR64等。常见的有PAR30、PAR38，功率有5×1W、7×1W、12×1W。无论PAR30还是PAR38，其使用的LED透镜的外形规格都是相同的，最大直径一般为19.8mm左右，卡口（台阶）直径为17.8mm左右。3）PAR灯透镜的安装，除了利用灯杯前部面板卡VI固定外，透镜的小内口与LED的接触方式也有两种。2）PAR灯透镜以38°应用得最多。......
2023-06-15
-
表面淬火的定义及应用场景详细阅读
由于上述加热方法各有其特点及局限性，故均在一定条件下获得应用，其中应用最普遍的是感应加热表面淬火及火焰加热表面淬火。高碳钢表面淬火后，尽管表面硬度和耐磨性提高了，但心部的塑性及韧性较低，因此高碳钢的表面淬火主要用于承受较小冲击和交变载荷下工作的工具、量具及高冷硬轧辊。低碳钢表面淬火后强化效果不显著，故很少应用。......
2023-06-24
相关推荐