在一般情况下相贯线是一条封闭的空间曲线，但有时它可能退化为一条平面曲线。图5-16正交的两等直径圆柱体相贯常见的相贯线特殊情况有以下几种。但其相贯线的水平投影是没有积聚性的，仍为两个椭圆。图5-17相贯线的特殊情况选择适当的辅助面。先画相贯线上能求出的特殊点。......
2025-09-29
两曲面体相交线的绘制
【摘要】：两曲面体的相贯线一般情况下是封闭的光滑的空间曲线，特殊情况下可能为平面曲线或直线。求两曲面体的相贯线，一般要先作出一系列的相贯点，然后顺次光滑地连接成曲线。两曲面投影同时可见的部分，此段相贯线才是可见的，应画为实线，否则是不可见的应画为虚线。例6—15求作两圆柱的相贯线。无论是实体还是虚体，相贯线的作法均相同。图6—24作圆柱和圆锥的相贯线判别相贯线的可见性。
两曲面体的相贯线一般情况下是封闭的光滑的空间曲线，特殊情况下可能为平面曲线或直线。求两曲面体的相贯线，一般要先作出一系列的相贯点，然后顺次光滑地连接成曲线。相贯点是两曲面的共有点，要根据两曲面的形状、大小、位置以及投影特性来作图，一般有两种作法。
（1）积聚投影法——当曲面体表面的某投影有积聚性时，则相贯线的一个投影与此重合而成为已知，于是求其他投影时就可利用在另一曲面上取点的方法作出。
（2）辅助面法——根据三面共点原理，作辅助面与两曲面相交，求出两辅助截交线的交点，即为相贯点。通常选择平面作为辅助面，并使其与两曲面的截交线的投影成为直线或圆，才能使作图简便、准确，否则无实用意义。
为了准确地画出相贯线，首先需要作出控制相贯线形状和范围的一些特殊位置的相贯点，如最高、最低、最左、最右、最前、最后点，以及曲面投影轮廓线上的点等，其次还要作出若干中间位置的相贯点。
将各相贯点连接成相贯线的规则是：只有对于两曲面都是相邻的两个相贯点，才可以相连。当曲面的某投影有积聚性时，可利用前述积聚投影编号的方法来确定连点的次序。
两曲面投影同时可见的部分，此段相贯线才是可见的，应画为实线，否则是不可见的应画为虚线。虚线和实线的分界点是曲面投影轮廓线上的相贯点。
例6—15 求作两圆柱的相贯线。
解 如图6—21所示，两圆柱的轴线垂直相交，小圆柱从上向下贯穿大圆柱，为全贯，相贯线是上下两条封闭的空间曲线。从投影图还可以看出相贯线是上下、左右、前后均对称的。由于小圆柱面的H投影和大圆柱面的W投影都有积聚性，实际上相贯线的H投影和W投影均为已知，现只需作出相贯线的V投影。
图6—21 两圆柱的相贯线
因上下两条相贯线的作法相同，这里仅叙述上面一条相贯线的作图步骤。
（1）先作特殊点。相贯线上最左点为Ⅰ，最右点为Ⅱ，它们同时为最高点。相贯线上最前点为Ⅲ，最后点为Ⅳ，它们又是最低点。这四个点可直接在H投影和W投影中确定，然后再作出它们的V投影。
（2）作若干中间点。可在最高点和最低点之间作水平辅助面，然后求出左右和前后对称的四个点A，B，C，D。
（3）将各点的V投影光滑地连成相贯线。
（4）相贯线的可见性判别。由于相贯线前后对称，V投影重合，故画为实线。
在上例中，若将小圆柱体看作为虚体，则在大圆柱体上就形成圆柱孔，如图6—22所示；若将两圆柱体均作为虚体，则就成为两圆柱孔的相交，如图6—23所示。无论是实体还是虚体，相贯线的作法均相同。
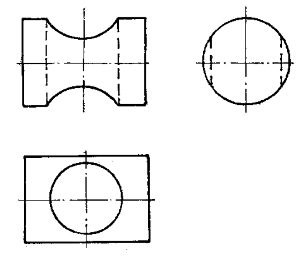(https://www.chuimin.cn)
图6—22 圆柱体上的圆柱孔
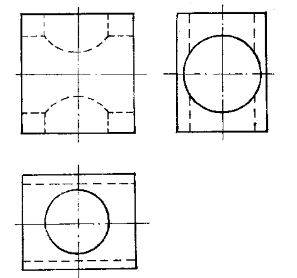
图6—23 两圆柱孔相交
例6—16 求作圆柱与圆锥的相贯线。
解 如图6—24所示，圆柱与圆锥的轴线是垂直交叉的，它们是互贯。相贯线为一条封闭的空间曲线，且左右对称。圆柱面的W投影有积聚性，相贯线的W投影为已知，需要作出其V投影和H投影。作图步骤如下：
（1）作圆锥W投影轮廓线上的点Ⅰ和Ⅱ，Ⅱ是最前点。
（2）作最高点Ⅲ，Ⅳ和最低点Ⅴ，Ⅵ，它们是圆柱V投影轮廓线上的点，也是虚实线的分界点。
（3）作最后点Ⅶ和Ⅷ，它们是圆柱H投影轮廓线上的点，也是虚实线的分界点。
（4）作圆锥V投影轮廓线上的点Ⅸ，Ⅹ，Ⅺ，Ⅻ。
（5）作若干中间点。本题可选择水平面作为辅助面，也可选择通过锥顶点的侧垂面作为辅助面，求出若干中间点（图略）。
（6）将各点连成相贯线。由于圆柱面的W投影有积聚性，可先在W投影中将各点标注编号，并注明可见性，然后从任一端点开始，依次连接可见的点，再返回连接不可见的点，最后回到起点。按此方法显示的连点次序如下：Ⅰ→Ⅲ→Ⅸ→Ⅶ→Ⅺ→Ⅴ→Ⅱ→Ⅵ→Ⅻ→Ⅷ→Ⅹ→Ⅳ→Ⅰ。分别将各点的V投影和H投影光滑连接成曲线，即得相贯线的V投影和H投影。
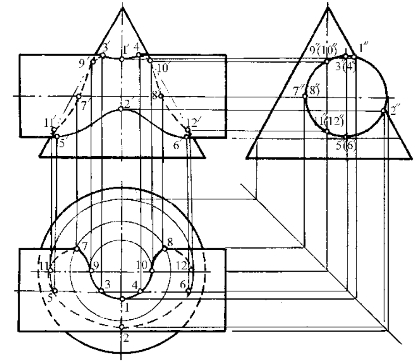
图6—24 作圆柱和圆锥的相贯线
（7）判别相贯线的可见性。在H投影中，圆锥面全部可见，再看圆柱面可知，上半圆柱面上的线7—9—3—1—4—10—8应画为实线，其余为虚线。在V投影中，位于前半圆锥面上且同时位于前半圆柱面上的线才可见，故3′—1′—4′和5′—2′—6′应画为实线，其余为虚线。
（8）最后处理圆柱和圆锥的投影轮廓线，完成全图。
相关文章
- 详细阅读
-
如何创建曲面相交特征：7.7曲面相交方法步骤详细阅读
显示两个曲面是否相交，以避免可能的间隙。创建曲面相交特征的具体方法与步骤如下：打开源文件第7章∣7-7.prt，曲面特征如图7-97所示。6）在模型树中右击曲面对其进行临时隐藏，可观看如图7-100所示的曲面相交线。图7-99 选择相交曲面图7-100 相交曲线7）单击模型树中的并单击组中的按钮，系统将弹出控制板；更改阵列类型为并选择曲面特征阵列轴，在角度方向栏输入阵列数目为“6”并对其进行360°均匀阵列。图7-103 顶点倒圆角图7-104 偏移曲面......
2025-09-29
-
平面与平面体的相交方法详细阅读
平面与立体表面的交线称为截交线，该平面称为截平面。平面体的截交线为多边形。平面截切平面体时，截交线在一个截平面内，截交线与截平面具有相同的投影特性。当截平面为特殊位置平面，截交线在其相应的投影面上的投影是已知的。图3.36平面立体求截交线如图3.37、所示，已知带切口的三棱锥S-ABC的正面投影，补全水平投影和侧面投影。由的方法求出截平面与棱线交点的投影以及截平面与截平面交点的投影，依次连接可得截交线。......
2025-09-30
-
平面与曲面的相交：立体几何优化详细阅读
平面立体与曲面立体的表面交线，一般是由数段平面曲线组合而成的空间曲线，如图4-18所示。因此，求作平面立体与曲面立体的相贯线，可归结为求作平面与曲面立体的截交线和求直线（棱线）与曲面立体表面的交点。其中除左边的棱面AB完全与半球相交外，其他两个棱面只部分与半球相交。因此，本题只需再作出相贯线的正面投影及侧面投影即可。......
2025-09-29
-
曲面体截交线-画法几何与土木工程制图详细阅读
曲面体的截交线一般情况下是平面曲线。当截平面与直纹曲面交于直素线，或与曲面体的平面部分相交时，截交线可为直线。因此求曲面体的截交线，实际上是作出曲面上的一系列的共有点，然后顺次连接成光滑的曲线。曲面体的投影轮廓线与截平面的交点，是截交线虚实线的分界点。3）球的截交线图6—12正平面与球相交无论截平面处于何种位置，它与球的截交线总是圆。例6—10求作铅垂面P与回转体的截交线。......
2025-09-30
-
绘制多段线命令POLYLINE详解详细阅读
多段线是AutoCAD绘图中比较常见的一种实体，通过绘制多段线，可以得到一个由若干直线和圆弧连接而成的折线或曲线。整条多段线是一个实体，可以统一对其进行编辑。另外，多段线中每段线条还可以设置为不同的线宽，因此，多段线也称为变宽线。执行POLYLINE命令可采用的三种方式：● 绘图工具栏 。图2-22闭合的多段线图2-23防爆荧光灯符号打开正交功能，先画一条长5个图形单位的竖线。启动绘制多段线命令。......
2025-09-29
-
曲面与地形面的交线分析详细阅读
求曲面与地形面的交线，即求曲面上与地形面上标高相同的等高线的交点，然后用平滑曲线顺次连接起来即得曲面与地面的交线。同理，由于填土部分的坡度为1∶1.5，故其平距为1.5个单位长度，据此便可作出填土部分平面坡面与坡面、坡面与地形面的两高程等高线的交点，顺次连接这些交点即得相邻边坡坡面的交线及各坡面与地形面的交线。根据填方和挖方的坡度算出同坡曲面上等高线的平距，作出同坡曲面上的等高线。......
2025-09-29
-
相交线与平行线的数学知识大揭秘详细阅读
利玛窦与徐光启明代徐光启与意大利传教士利玛窦合作,翻译出版了欧几里得的《几何原本》,西方数学开始传入中国．左图即为利玛窦与徐光启合影．徐光启评价该书说:“此书有四不必:不必疑,不必揣,不必试,不必改．有四不可得:欲脱之不可得,欲驳之不可得,欲减之不可得,欲前后置之不可得．”知能概述相交或平行是同一平面内两条直线的基本位置关系．当两条直线相交或分别与第三条直线相交,就产生对顶角、同位角、内错角、同旁......
2025-09-29
相关推荐