1）直线的表示法在标高投影中，直线的位置是由直线上的两个点或直线上一点及该直线的方向确定。图9—4求线段的实长与倾角在实际工作中，常遇到直线两端的标高投影的高程并非整数，需要在直线的标高投影上作出各整数标高点。例9—2如图9—5所示，已知直线AB的标高投影a4.3b7.8，求直线上各整数标高点。解平行于直线AB作一辅助的铅垂面，采用标高投影比例尺作相应高程的水平线，最高一条为8，最低一条为4。......
2023-09-24
棱柱体投影技巧-画法几何及土木工程制图
【摘要】：画棱柱体的投影时，一般是使其侧棱线垂直于某投影面。如图6—1a所示，正五棱柱在三面投影体系中的位置：顶面和底面是水平面且为正五边形，五个侧棱面均为矩形，除后侧棱面是正平面外，其余均是铅垂面，五条侧棱线均是铅垂线。图6—1正五棱柱的投影在棱柱面上取点和线，可利用有积聚性的投影来作图。例6—1如图6—2a所示，已知五棱柱面上A点的V投影a′和CD线的V投影c′d′，求作它们的其他两投影。
画棱柱体的投影时，一般是使其侧棱线垂直于某投影面。如图6—1a所示，正五棱柱在三面投影体系中的位置：顶面和底面是水平面且为正五边形，五个侧棱面均为矩形，除后侧棱面是正平面外，其余均是铅垂面，五条侧棱线均是铅垂线。
运用点线面的投影规律，作出正五棱柱的三面投影如图6—1b所示。其H投影为正五边形，它是顶面和底面的重合投影，且反映实形；它的五条边是五个侧棱面的积聚投影，五个顶点是五条侧棱线的积聚投影。对于H投影而言，顶面可见而底面不可见。其V投影是由矩形线框组成，它的上下两段水平线分别是顶面和底面的积聚投影；五个侧棱面中，除了后侧棱面的投影反映实形外，另四个的投影均为类似图形；五条侧棱线的投影均反映实长。对于V投影而言，前方两个侧棱面可见，后方三个侧棱面不可见，故它们的交线应画成虚线。其W投影也是由矩形线框组成，它的上下两边分别是顶面和底面的积聚投影；最后方的侧棱面积聚为直线，左方两侧棱面与右方两侧棱面的投影完全重合，且左面可见，右面不可见，故左侧棱线应画为实线，右侧棱线应画为虚线，但两线重合只画出实线。
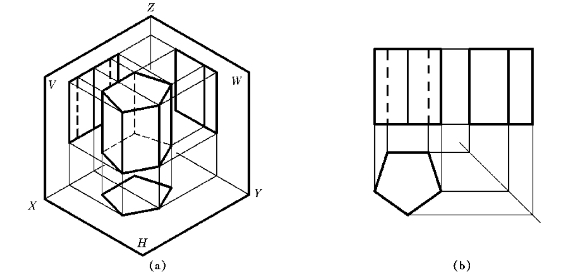
图6—1 正五棱柱的投影
在棱柱面上取点和线，可利用有积聚性的投影来作图。
例6—1 如图6—2a所示，已知五棱柱面上A点的V投影a′和CD线的V投影c′d′，求作它们的其他两投影。
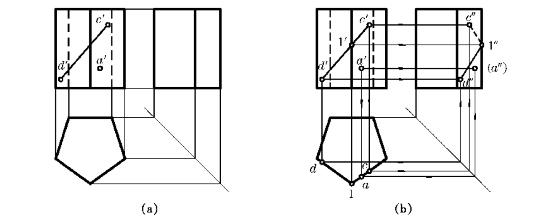
图6—2 正五棱柱面上取点和线
解 作图步骤如图6—2b所示：
（1）作A点的投影
由a′可知，A点在右前方的侧棱面上，于是先在H投影中定出a，然后作出（a″），（a″）不可见。
（2）作CD线的投影
由于c″d″是实线，可知CD在前方的左右两个侧棱面上，与最前棱线的交点Ⅰ为转折点，所以CD实际上是折线，由CⅠ和DⅠ两条直线构成。先在H投影中作出c1d，再作出c″1″d″。因c″1″不可见应画为虚线，d″1″为实线。
有关画法几何及土木工程制图（第4版）的文章
- 详细阅读
-
点的透视投影-画法几何及土木工程制图详细阅读
1）点的透视投影仍然为一点点的透视就是过该点的视线与画面的交点。A点的透视A°与其基透视a°的连线A°a°，其长度称为A点的透视高度，它是点A的实际高度Aa的透视，一般情况下不与实际高度相等。图8—5点的透视作图......
2023-09-24
-
投影图选择-画法几何及土木工程制图详细阅读
投影图选择的原则是用较少的投影图把物体的形状完整、清楚、准确地表达出来。投影图选择包括确定物体的放置位置、选择正面投影及确定投影图数量等三个问题。此外还应尽量减少投影图中的虚线及合理利用图纸。图11—8正面投影的选择图11—9a，b为一涵洞端墙及其形体分析，图11—9c，d为该涵洞端墙的两种布置情况。如图11—10a所示的沉井，习惯上只需用两个投影图，侧面投影是多余的。......
2023-09-24
-
点的三面投影—画法几何及土木工程制图详细阅读
将三个投影面展开后得到的三面投影图如图2—2b，c。以上所述点的三面投影特性，也正是形体投影图中“长对正、高平齐、宽相等”的理论依据。例2—1如图2—3a所示，已知B点的V投影b′和W投影b″，求其H投影b。......
2023-09-24
-
棱锥体投影技巧-画法几何与土木工程制图详细阅读
画棱锥的投影时，常使其底面平行于某投影面。如图6—3a所示，三棱锥在三面投影体系中的位置：底面△ABC是水平面，三个侧棱面△SAB，△SBC，△SAC均为一般位置平面；三条侧棱线均通过顶点S，SA是一般线，SB是侧平线，SC是正平线。图6—3三棱锥的投影该三棱锥的投影如图6—3b所示。例6—2如图6—4a所示，已知三棱锥面上点K的H投影k和直线MN的V投影m′n′，求作它们的其他两投影。......
2023-09-24
-
直线透视投影方法画法几何及土木工程制图详细阅读
1）直线的透视特性直线的透视及基透视，一般情况下仍是直线。迹点的透视即为其本身，其基透视则在基线上。直线的透视必通过直线的画面迹点，直线的基透视必通过该迹点在基面上的正投影。直线上离画面无穷远点的透视，称为直线的灭点，直线的透视延长后一定通过灭点。把直线的迹点和灭点相连可得直线的全长透视。......
2023-09-24
-
投影变换解题举例书名：画法几何及土木工程制图详细阅读
根据换面法和旋转法的基本原理，可将一般位置的直线和平面变换到特殊位置，以达到解题的目的。由于本题中AB和CD均为一般线，不能直接作出公垂线的投影，若把其中任一直线变换为与投影面垂直时，可根据其积聚投影作出公垂线和距离，为此需要经过两次变换，现用换面法作图。......
2023-09-24
-
平面旋转技巧-《画法几何及土木工程制图》详细阅读
为了将平面旋转到有利于解题的特殊位置，关键是确定旋转轴的位置和选择适当的旋转角度。2）将投影面垂直面旋转成投影面平行面以正垂线为旋转轴，可将正垂面旋转为水平面，其H投影反映实形。如图4—20所示，△ABC为正垂面，绕通过B点的正垂轴旋转，使其变换为水平面△A1BC1，于是△a1bc1≌△ABC。图4—21一般面旋转为水平面......
2023-09-24
相关推荐