例5—4已知环面上F点的V投影f′，求作F点的H投影和W投影。解作图步骤如图5—15所示：由于f′可见，F点一定在前半个外环面上。在V投影中，过f′作水平线与外环面的投影轮廓线相交，交点间的长度即为辅助圆的直径；在H投影中作出辅助圆的实形，由F在此圆上定出f，再作出（f″）；图5—15环面上取点因F点在上半环面上，故f可见；又因F点在右半个外环面上，故（f″）不可见。......
2023-09-24
画法几何：圆锥面上的素线和投影计算
【摘要】：圆锥面上的素线均相交于其顶点S。由于圆锥面是光滑的，和圆柱面类似，当素线的投影不是轮廓线时，均不画出。图5—11圆锥面上取点例5—2已知圆锥面上M点的V投影m′，求作其H和W投影m和m″。由m′可知，点M在前半圆锥面上，过m′作s′n′，再作出sn和s″n″；根据m′在s′n′上，可在sn上定m，在s″n″上定m″；由于M点在左半圆锥面上，故m和m″均是可见的。
1）圆锥面的形成
如图5—10a所示，直母线SA绕与其相交于S点的轴线O旋转而形成的曲面，称为圆锥面。母线的端点S为圆锥的顶点，另一端点A旋转形成底圆。圆锥面上的素线均相交于其顶点S。
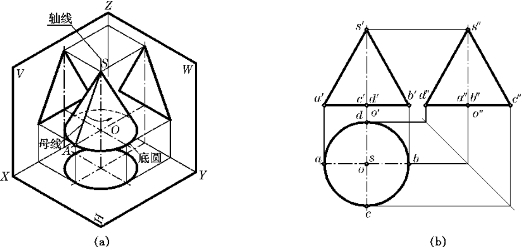
图5—10 圆锥面的形成及投影
2）圆锥面的投影
如图5—10b所示，当圆锥的轴线垂直于H面时，其H投影为圆，它是底圆的投影，其V投影和W投影均为等腰三角形，三角形的底边是底圆的积聚投影。V面投影图的轮廓线s′a′和s′b′分别是圆锥面上最左素线SA和最右素线SB的V投影，SA和SB将圆锥面分为前后两部分，向V面投影时，前半部分可见，后半部分不可见。W面投影图的轮廓线s″c″和s″d″分别是最前素线SC和最后素线SD的W投影，SC和SD将圆锥面分为左右两部分，向W面投影时，左半部分可见，右半部分不可见。由于圆锥面是光滑的，和圆柱面类似，当素线的投影不是轮廓线时，均不画出。
3）圆锥面上取点
由于圆锥面的三个投影均无积聚性，所以在圆锥面上取点一般必须利用辅助线来作图，通常可采用素线法或纬圆法，如图5—11a所示。
图5—11 圆锥面上取点
例5—2 已知圆锥面上M点的V投影m′，求作其H和W投影m和m″。
解 素线法作图如图5—11b所示：
选择通过已知点M的素线SN作为辅助线。
（1）由m′可知，点M在前半圆锥面上，过m′作s′n′，再作出sn和s″n″；
（2）根据m′在s′n′上，可在sn上定m，在s″n″上定m″；
（3）由于M点在左半圆锥面上，故m和m″均是可见的。
纬圆法作图如图5—11c所示：
选择通过已知点M的纬圆作为辅助线。
（1）过m′作水平线与V投影轮廓线相交，从而确定纬圆的直径；
（2）在H投影中作出该纬圆的实形，由m′作投影连线在此圆周上定出m，再作出m″。同理m和m″均可见。
有关画法几何及土木工程制图（第4版）的文章
- 详细阅读
-
圆锥体的投影及其性质详细阅读
图4-21圆锥体的三视图根据以上分析可知：轴线为铅垂线的圆锥体的俯视图为圆，主视图和左视图为相同的等腰三角形；圆锥面的三个投影都没有积聚性。图4-22圆锥表面上的点2）纬圆法用垂直于回转体轴线的截平面截切回转体，其交线一定是圆，称为“纬圆”。......
2023-06-28
-
圆锥的侧面积和全面积计算详细阅读
如果圆锥的母线长为l，底面半径为r，那么圆锥侧面展开的扇形半径为________，扇形的弧长为________，圆锥的侧面积为________，圆锥的全面积为_________．1．若将半径为24cm的半圆形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为（ ）．A．3cm B．6cm C．12cm D．24cm2．已知圆锥底面圆的半径为6m，它的侧面积为60πcm2，则这个圆锥的高是（ ）．A．......
2023-07-03
-
圆柱体：素线和三视图分析详细阅读
直线AA1称为母线，圆柱面上任何一条平行于轴线OO1的直线，均称为圆柱面的素线。图4-20圆柱体的三视图根据以上分析，轴线为铅垂线的圆柱体的俯视图为一个圆，主视图和左视图为相同的矩形。......
2023-06-28
-
画法几何：球面形成及投影求解详细阅读
1）球面的形成如图5—12a所示，以圆为母线，绕其直径旋转而形成的曲面称为球面。例5—3如图5—13a所示，已知球面上D点的W投影d″和E点的H投影e，求作D点和E点的其他两投影。过e作水平线，与H投影的轮廓线相交，交点间长度即为辅助圆的直径。在V投影中作出辅助圆的实形，并根据E在此圆上定出（e′），然后再作出e″。由于E点在球面的上、后、左部分，故（e′）不可见，e″可见。......
2023-09-24
-
圆锥体截交线优化解析详细阅读
图4-32正垂面与横放圆锥体的截交线分析如图4-32所示，圆锥的轴线为侧垂线，β＞α，其截交线是一个椭圆，它的正面投影积聚成一直线，而其水平投影和侧面投影则仍为椭圆。根据圆锥的投影特性可知：截交线椭圆的侧面投影全部可见，截平面与前、后素线的交点A、B为截交线水平投影可见与不可见部分的分界点，位于下半圆锥面上的截交线不可见。例4-14求铅垂面PH与圆锥体的截交线。......
2023-06-28
-
点的透视投影-画法几何及土木工程制图详细阅读
1）点的透视投影仍然为一点点的透视就是过该点的视线与画面的交点。A点的透视A°与其基透视a°的连线A°a°，其长度称为A点的透视高度，它是点A的实际高度Aa的透视，一般情况下不与实际高度相等。图8—5点的透视作图......
2023-09-24
-
平面标高投影：画法几何及土木制图详细阅读
1）平面上的等高线和坡度线标高投影中，预定高度的水平面与所表示表面的截交线称为等高线。图9—6b为平面P上的一系列等高线的标高投影。2）平面的表示法在正投影中所介绍的用几何元素表示平面的方法在标高投影中仍然适用。但要注意的是，在用坡度比例尺表示平面时，标高投影的比例尺或比例要同时给出。图9—11作已知平面的等高线3）平面与平面的交线在标高投影中，求两平面的交线，通常采用水平面作为辅助面。......
2023-09-24
相关推荐