1）几何元素表示平面由几何公理可知，在空间不属于同一直线上的三点确定一平面。2）迹线表示平面平面与投影面的交线称为迹线。如图2—28所示，P平面与H面、V面、W面的交线分别称为水平迹线PH、正面迹线PV、侧面迹线PW。迹线是投影面内的直线，它的一个投影就是其本身，另两个投影与投影轴重合，用迹线表示平面时，是用迹线本身的投影来表示的。任意两条迹线都可以确定平面的空间位置，实质上就是两相交直线表示平面的特例。......
2025-09-30
圆柱面的画法及投影-画法几何及土木工程制图
【摘要】：1）圆柱面的形成如图5—8a所示，直母线AA1绕与其平行的轴线O旋转而形成的曲面，称为圆柱面。例5—1如图5—9a所示，已知圆柱面上E点和F点的V投影（e′）和f′，作出E点和F点的其他两投影。图5—9圆柱面上取点解作图步骤如图5—9b所示：由（e′）不可见，可知E点在后半圆柱面上；由f′可见，可知F点在前半圆柱面上。
1）圆柱面的形成
如图5—8a所示，直母线AA1绕与其平行的轴线O旋转而形成的曲面，称为圆柱面。母线两端点A和A1旋转时形成顶圆和底圆。圆柱面上的素线互相平行。
图5—8 圆柱面的形成及投影
2）圆柱面的投影
如图5—8b所示，当圆柱面的轴线垂直于H面时，其H投影为圆，它是整个圆柱面的积聚性投影。其V投影和W投影均为矩形，矩形的上下两水平线是顶圆和底圆的投影。V面投影图的轮廓线a′a′1和b′b′1，分别是圆柱面上最左素线AA1和最右素线BB1的V投影。AA1和BB1将圆柱面分为前后两部分，向V面投影时，前半部分可见，后半部分不可见，所以V面投影矩形实际是圆柱面前后两部分投影的重叠。W面投影图的轮廓线c″c″1和d″d″1，分别是最前素线CC1和最后素线DD1的W投影。CC1和DD1将圆柱面分为左右两部分，W面投影矩形是圆柱面左右两部分投影的重叠，向W投影时，左半部分可见，右半部分不可见。
在曲面的投影图中，凡处于可见部分的点和线是可见的，否则是不可见的，当需要表示可见性时，将不可见点的投影字母加括号表示，不可见线画为虚线。
AA1和BB1的W投影a″a″1和b″b″1与轴线的投影o″重合，CC1和DD1的V投影c′c′1和d′d′1与轴线的投影o′重合，由于圆柱面是光滑的曲面，故规定这些素线的投影不处于轮廓位置时，均不画出。
3）圆柱面上取点(https://www.chuimin.cn)
在圆柱面上取点，可直接利用圆柱面的积聚性投影来作图。
例5—1 如图5—9a所示，已知圆柱面上E点和F点的V投影（e′）和f′，作出E点和F点的其他两投影。
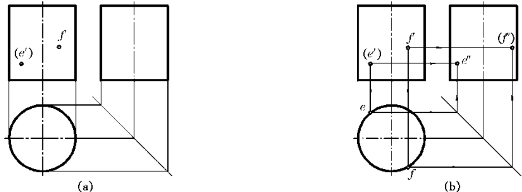
图5—9 圆柱面上取点
解 作图步骤如图5—9b所示：
（1）由（e′）不可见，可知E点在后半圆柱面上；由f′可见，可知F点在前半圆柱面上。于是在H投影圆周上定出e和f。
（2）根据（e′）和e作出e″，因E点在左半圆柱面上，故e″可见；根据f′和f作出（f″），因F点在右半圆柱面上，故（f″）不可见。
相关文章
- 详细阅读
-
直线旋转技巧-画法几何及土木工程制图详细阅读
由此，可总结出直线的旋转规律如下：图4—14直线的旋转若直线绕垂直于某投影面的轴旋转时，则其在该投影面上的投影长度不变，且其对该投影面的倾角亦不变。为了将直线旋转到有利于解题的特殊位置，选择旋转轴和旋转角度至关重要。图4—16正平线旋转为铅垂线3）将一般位置直线旋转成投影面垂直线综合上述两种旋转的情况，可以连续作两次旋转，第一次将一般线旋转为投影面平行线，第二次将其旋转成投影面垂直线。......
2025-09-30
-
直线变换法则-画法几何及土木工程制图详细阅读
图4—5一般线变换为H1面平行线2）将投影面平行线变换为新投影面垂直线这时新投影面必须垂直于该直线，于是该直线的新投影有积聚性。图4—7正平线变换为H1垂直线3）将一般位置直线变换成新投影面垂直线综合上述两种变换的情况，可连续作两次换面，第一次将一般线变换为新投影面的平行线，第二次将其变换为新投影面的垂直线。图4—8一般线变换为投影面垂直线......
2025-09-30
-
直线上的点-《画法几何及土木工程制图》详细阅读
如图2—15中直线AB上有一点K，通过K点作垂直于H面的投射线Kk，它必在通过AB的投射平面ABba内，故K点的H面投影k必在AB的投影ab上。2）定比性关系直线上的点将直线分为几段，各线段长度之比等于它们的同面投影长度之比。图2—15直线上的点的投影例2—5如图2—16a所示，已知ab和a′b′，求直线AB上K点的投影，使AK∶KB＝2∶3。边a′任作一直线，在其上量取：a′1＝am，a′2＝an，a′3＝ab。......
2025-09-30
-
各种位置直线-画法几何及土木工程制图详细阅读
为了详细研究直线的投影性质，可按直线与三个投影面的相对位置，将其分为三类：一般位置直线、投影面平行线、投影面垂直线。后两类统称为特殊位置直线。图2—10一般位置直线2）投影面平行线只平行于一个投影面，且倾斜于另外两个投影面的直线，称为投影面平行线。表2—2投影面垂直线例2—3如图2—11a所示，已知A点的两面投影，正平线AB＝20，且α＝30°，作出直线AB的三面投影。......
2025-09-30
-
平面旋转技巧-《画法几何及土木工程制图》详细阅读
为了将平面旋转到有利于解题的特殊位置，关键是确定旋转轴的位置和选择适当的旋转角度。2）将投影面垂直面旋转成投影面平行面以正垂线为旋转轴，可将正垂面旋转为水平面，其H投影反映实形。如图4—20所示，△ABC为正垂面，绕通过B点的正垂轴旋转，使其变换为水平面△A1BC1，于是△a1bc1≌△ABC。图4—21一般面旋转为水平面......
2025-09-30
-
两直线相对位置-画法几何及土木工程制图详细阅读
两直线之间的基本相对位置有三种：平行、相交、交叉。图2—20两直线相交反之，若两直线的三组同面投影均相交，且交点符合点的投影规律，则空间两直线必相交。图2—21判别两直线是否相交解一般情况下，根据V和H两投影就可判定是否相交，但若两直线中有一条是侧平线，则需要作出W投影。所以在这里仅讨论两直线垂直相交时的投影特性，所得结论对于两直线垂直交叉时仍同样适用。......
2025-09-30
-
综合题的分析与作图-《画法几何及土木工程制图详细阅读
图3—27求作符合条件的直线解空间分析：过M点与△ABC平行的直线有无数条，其轨迹是与△ABC平行的平面，由此可先作出这个与△ABC平行的轨迹平面P，然后作出平面P与直线DE的交点N，M和N的连线即为所求。......
2025-09-30
相关推荐