图15—9培训楼基础布置平面图整板基础包括基础板、板上基础梁和柱基，除基础梁和柱需另绘详图外，基础板的配筋是直接绘制在平面图上的。板底沿横向和纵向配置了受力筋，其规格为14＠160和16＠160，板顶也配置了双向受力筋规格为12＠160和14＠160。①～②和～轴线范围是电梯井坑基础，坑底部标高为—1.400m。图15—11是条形基础详图。基础上部是基础柱，尺寸450mm×400mm。平面图用局部剖面表示基础中双向钢筋的布置为φ8＠150和φ8＠130。......
2023-09-24
投影变换解题举例书名：画法几何及土木工程制图
【摘要】：根据换面法和旋转法的基本原理，可将一般位置的直线和平面变换到特殊位置，以达到解题的目的。由于本题中AB和CD均为一般线，不能直接作出公垂线的投影，若把其中任一直线变换为与投影面垂直时，可根据其积聚投影作出公垂线和距离，为此需要经过两次变换，现用换面法作图。
根据换面法和旋转法的基本原理，可将一般位置的直线和平面变换到特殊位置，以达到解题的目的。前面已对点、直线、平面的基本变换作了详细介绍，这些方法概念清楚，作图简便，是解题的基础。对于各种各样的问题，解法并非千篇一律，而是要根据题目所给定的具体条件进行分析灵活运用。一般在解题时，首先进行空间分析，确定解题的方法和步骤，然后按次序作图，直至求出答案。
下面的一些例题，解法可能有多种，这里仅作出常用的一种解法。通过这些示例，可以举一反三，融会贯通，掌握解题的基本方法，培养分析问题和解决问题的能力。
例4—1 如图4—22a所示，已知矩形的一边AB[ab，a′b′]和其邻边BC的H投影bc，试补全此矩形ABCD的投影。
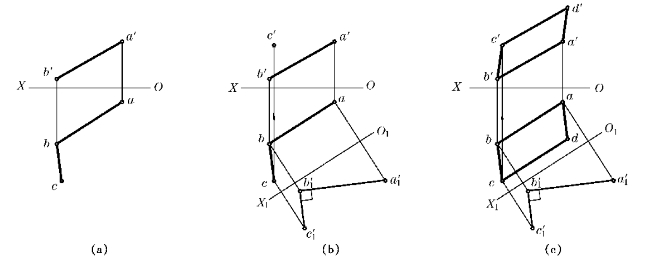
图4—22 用换面法补全矩形ABCD的投影
解 空间分析：
矩形的邻边互相垂直，即AB⊥BC，若将AB变换为投影面平行线，则可利用直角投影定理作出BC，然后根据矩形对边平行的特点，完成其投影图。下面分别用换面法和旋转法来作图。
换面法作图步骤如图4—22b，c所示：
（1）用V1代换V面，令V1∥AB且V1⊥H，则O1X1∥ab，作出a′1b′1；
（2）过b′1作a′1b′1的垂线，与过c的投影连线相交于c′1；
（3）返回到V面作出c′，于是得到b′c′；
（4）作c′d′∥b′a′，a′d′∥b′c′和cd∥ba，ad∥bc，完成矩形ABCD的投影。
旋转法作图步骤如图4—23所示：
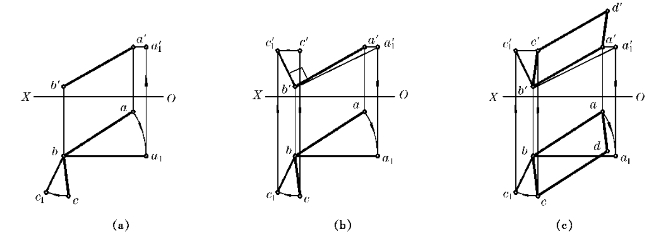
图4—23 用旋转法补全矩形ABCD的投影
（1）以过B点的铅垂线为旋转轴，将AB旋转为正平线A1B，由a1b∥OX，作出a′1b′，BC应作相同的旋转，作出bc1；
（2）过b′作a′1b′的垂线，与过c1的投影连线相交于c′1；
（3）将BC1作反方向旋转，可求出b′c′；
（4）根据对边互相平行作出矩形的另两条边。
由上例可以看出，换面法和旋转法的解题思路是相同的，只是作图方法不同而已，故一般的问题用换面法和旋转法都可以解。
在充分理解换面法和旋转法的作图原理以后，有时还可以把两种方法结合起来解题。
例4—2 如图4—24a所示，已知两相交直线AB和BC，求它们的夹角∠ABC的真实大小。
解 空间分析：
两相交直线AB和BC确定一个平面，若将该平面变换为投影面平行面时，则能反映∠ABC的真实大小。由于平面ABC是一般位置，必须经过两次变换，本题在这里第一次用换面法作图，第二次用旋转法作图。
作图步骤：
（1）用V1代换V面，先作出△ABC内的水平线AD，令V1⊥H且V1⊥AD，于是O1X1⊥ad，则a1b1c1积聚为直线，如图4—24b所示；
（2）令旋转轴通过C1点且垂直于V1面，将a′1b′1c′1旋转到与O1X1平行，即a′2b′2c′1∥O1X1，然后作出∠a2b2c，则∠a2b2c为∠ABC的真实大小，如图4—24c所示。
由此可见，恰当地利用换面法和旋转法的特点，可以使作图更简捷。但是一般来说，旋转法需要作角度，不太方便，且作图又容易重叠，不如换面法清楚，所以解题最常用的还是换面法。
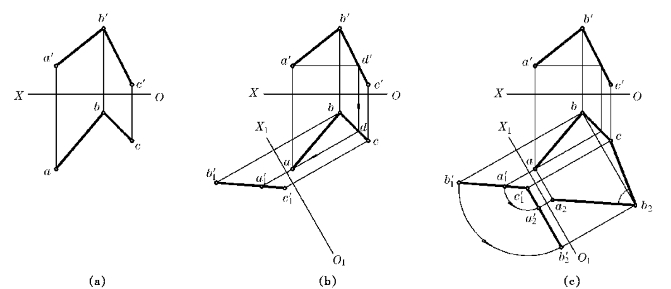
图4—24 求角度∠ABC的真实大小
例4—3 如图4—25a所示，求两交叉直线AB和CD的公垂线MN及距离。
解 空间分析：
公垂线MN应与AB和CD均垂直，其实长即所求实际距离。由于本题中AB和CD均为一般线，不能直接作出公垂线的投影，若把其中任一直线变换为与投影面垂直时，可根据其积聚投影作出公垂线和距离，为此需要经过两次变换，现用换面法作图。
作图步骤如图4—25b，c所示：
（1）用V1代换V面，令V1∥CD且V1⊥H，于是O1X1∥cd，作出c′1d′1和a′1b′1；
（2）用H2代换H面，令H2⊥CD且H2⊥V1，于是O2X2⊥c′1d′1，作出c2d2和a2b2；
（3）由于c2d2积聚为一点，公垂线上N点的投影n2亦重合于此点，过此点作m2n2⊥a2b2，得垂足m2，m2n2为公垂线MN的投影，且反映其实长即距离；
（4）过m2作垂直于O2X2的投影连线，交a′1b′1于m′1，然后作m′1n′1∥O2X2，交c′1d′1于n′1；
（5）返回到H面和V面上，依次作出mn和m′n′，MN即所求公垂线。
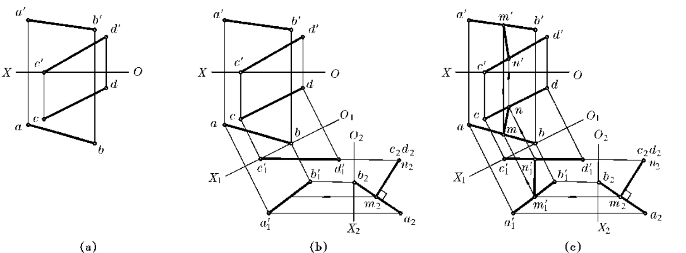
图4—25 求两交叉直线的公垂线及距离
例4—4 如图4—26a所示，已知AB∥CD，且距离为15，求作CD的水平投影cd。
解 空间分析：
若经过两次换面，将两平行线AB和CD变换为投影面垂直线，则在该投影面上它们的投影有积聚性，且反映真实距离。这时可定出CD的位置，然后返回到H面中作出cd。
作图步骤如图4—26b，c所示：
（1）令O1X1∥a′b′，作出a1b1；
（2）令O2X2⊥a1b1，作出a′2b′2；
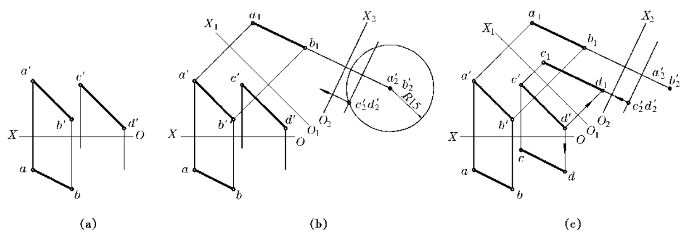
图4—26 补全直线CD的投影
（3）以a′2b′2为圆心，作R＝15mm的圆，c′2d′2必在此圆周上；以c′d′到O1X1的距离为长度作O2X2的平行线，交圆周于c′2d′2点；
（4）由c′2d′2返回到H面上作出cd。
本题有两解，图中只作出一解。
有关画法几何及土木工程制图（第4版）的文章
- 详细阅读
-
建筑透视图画法举例画法几何及土木工程制图详细阅读
例8—5已知房屋的平面图和立面图，如图8—36a所示，画出房屋的透视图。④布置画面，定出基线o′x′和视平线h—h。图8—36房屋透视图⑤求出透视平面图，在画面上作出真高线A°a，高度由立面图上量取，再求屋面透视，如图8—36c所示。图8—37拱桥透视图将前后立面可见轮廓线的透视相连接，省略被挡住部分的透视，完成全图。......
2023-09-24
-
钢屋架结构图举例示意《画法几何及土木工程制图详细阅读
图15—19钢屋架立面图从立面图可以看出，屋架的上、下弦分别由若干根杆件、节点板焊接而成，再用一些直杆和斜杆经节点板将上、下弦相连构成屋架。杆件、节点板应编号并标注定位尺寸。支座节点因比例小，杆件和节点板的形状、尺寸及连接形式都无法表达清楚，另绘有详图，用索引符号表示。绘图比例1∶20。2—2剖面显示杆件由两个相同的角钢组成，两角钢之间用塞焊与节点板相连，见放大的上弦塞焊图。......
2023-09-24
-
给水排水制图规定-画法几何及土木工程制图详细阅读
1）图线建筑给水排水制图采用的各种图线宜符合表16—1的规定。表16—2给水排水制图的比例在建筑给水排水轴测系统图中，如局部表示有困难时，该处可不按比例绘制。编号用分数形式表示，分子为管道类别代号，分母为管道进出口序号，标注方法见图16—11。建筑物内穿过楼层的立管，其数量多于一根时，宜用阿拉伯数字编号，表示形式为“管道类别和立管代号—编号”。表16—3给水排水制图常用图例......
2023-09-24
-
直线上的点-《画法几何及土木工程制图》详细阅读
如图2—15中直线AB上有一点K，通过K点作垂直于H面的投射线Kk，它必在通过AB的投射平面ABba内，故K点的H面投影k必在AB的投影ab上。2）定比性关系直线上的点将直线分为几段，各线段长度之比等于它们的同面投影长度之比。图2—15直线上的点的投影例2—5如图2—16a所示，已知ab和a′b′，求直线AB上K点的投影，使AK∶KB＝2∶3。边a′任作一直线，在其上量取：a′1＝am，a′2＝an，a′3＝ab。......
2023-09-24
-
画法几何及土木工程制图：路线平面图详细阅读
2）画法特点和表达内容路线平面图主要是表示路线的走向和平面线型状况，以及沿线两侧一定范围内的地形、地物等情况。如图19—1所示，为某公路从K3＋300至K5＋200段的路线平面图。在路线平面图上应画出指北针或测量坐标网，用来指明道路在该地区的方位与走向。在路线平面图中，转折处应注写交角点代号并依次编号，如JD6表示第6个交角点。图19—3路线平面图的拼接......
2023-09-24
-
直线标高投影：画法几何及土木工程制图详细阅读
1）直线的表示法在标高投影中，直线的位置是由直线上的两个点或直线上一点及该直线的方向确定。图9—4求线段的实长与倾角在实际工作中，常遇到直线两端的标高投影的高程并非整数，需要在直线的标高投影上作出各整数标高点。例9—2如图9—5所示，已知直线AB的标高投影a4.3b7.8，求直线上各整数标高点。解平行于直线AB作一辅助的铅垂面，采用标高投影比例尺作相应高程的水平线，最高一条为8，最低一条为4。......
2023-09-24
-
常用绘图命令及用法-画法几何及土木工程制图详细阅读
例13—1绘制如图13—6所示的多边形。绘制结果如图13—7所示，具体操作如下：图13—7画圆命令的用法命令：CIRCLE↙。11）绘制云线命令：REVCLOUD↙或单击图标说明：使用多段线绘制修订云线。图13—8图案填充临时选项卡例13—3练习在图13—7中指定的区域绘制剖面线。如果该命令执行后，根据提示输入选项“T”，则弹出“图案填充和渐变色”对话框。......
2023-09-24
相关推荐