为了将平面旋转到有利于解题的特殊位置，关键是确定旋转轴的位置和选择适当的旋转角度。2）将投影面垂直面旋转成投影面平行面以正垂线为旋转轴，可将正垂面旋转为水平面，其H投影反映实形。如图4—20所示，△ABC为正垂面，绕通过B点的正垂轴旋转，使其变换为水平面△A1BC1，于是△a1bc1≌△ABC。图4—21一般面旋转为水平面......
2023-09-24
直线旋转技巧-画法几何及土木工程制图
【摘要】：由此，可总结出直线的旋转规律如下：图4—14直线的旋转若直线绕垂直于某投影面的轴旋转时，则其在该投影面上的投影长度不变，且其对该投影面的倾角亦不变。为了将直线旋转到有利于解题的特殊位置，选择旋转轴和旋转角度至关重要。图4—16正平线旋转为铅垂线3）将一般位置直线旋转成投影面垂直线综合上述两种旋转的情况，可以连续作两次旋转，第一次将一般线旋转为投影面平行线，第二次将其旋转成投影面垂直线。
直线的旋转，只要将直线上两端点绕同轴作同向同角度旋转，作出它们的新投影后，将同面投影相连即得直线旋转后的新投影。
如图4—14所示，直线AB绕铅垂轴O反时针旋转φ角，到达A1B1位置。根据点的旋转规律作出A1和B1的投影，然后同面投影相连，即得a1b1和a′1b′1。由作图过程可以看出，因oa＝oa1，ob＝ob1，∠aoa1＝∠bob1＝φ，即有∠aob＝∠a1ob1，故△aob≌△a1ob1，所以a1b1＝ab。这说明了直线绕铅垂轴旋转时，其H投影长度不变，且对H面的倾角α亦不变，但其V投影长度和β角都改变了。
同理，当直线绕正垂轴旋转时，其V投影长度不变，其β角亦不变。
由此，可总结出直线的旋转规律如下：
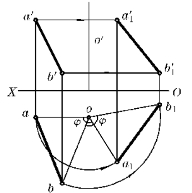
图4—14 直线的旋转
若直线绕垂直于某投影面的轴旋转时，则其在该投影面上的投影长度不变，且其对该投影面的倾角亦不变。
为了将直线旋转到有利于解题的特殊位置，选择旋转轴和旋转角度至关重要。直线的旋转有三种基本情况，现分述如下：
1）将一般位置直线旋转成投影面平行线
以铅垂线为旋转轴，可将一般线旋转成正平线，于是其V投影反映实长和α角。
如图4—15所示，一般线AB绕铅垂轴旋转。为了作图简便，可使旋转轴通过A点，旋转时A点位置不变，其投影亦不变。将AB旋转到正平线AB1的位置，这时只需作出B1点的投影，于是ab1∥OX，且ab1＝ab，则a′b′1＝AB，且∠a′b′1b′＝α。
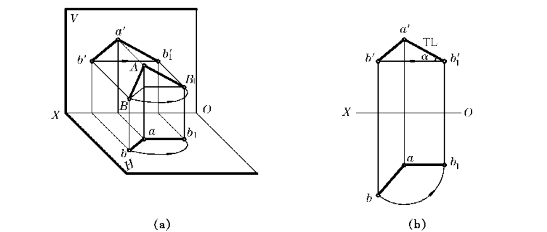
图4—15 一般线旋转为正平线
同理，若以正垂线为旋转轴，可将一般线旋转成水平线，并求出其实长和β角。
2）将投影面平行线旋转成投影面垂直线
以正垂线为旋转轴，可将正平线旋转成铅垂线，于是其H投影积聚为一点。
如图4—16所示，正平线AB绕通过B点的正垂轴，旋转到铅垂线A1B的位置，于是a′1b′⊥OX，a1b积聚为一点。
同理，以铅垂线为旋转轴，可将水平线旋转成正垂线，使其V投影积聚为一点。
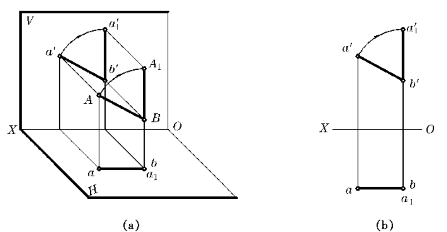
图4—16 正平线旋转为铅垂线
3）将一般位置直线旋转成投影面垂直线
综合上述两种旋转的情况，可以连续作两次旋转，第一次将一般线旋转为投影面平行线，第二次将其旋转成投影面垂直线。
如图4—17所示，AB是一般线。第一次将AB绕通过A点的铅垂轴旋转，使其变换为正平线AB1，a′b′1反映实长和α角；第二次将AB1绕通过B1点的正垂轴旋转，使其变换为铅垂线A2B1，于是a2b1积聚为一点。
同理，若AB第一次绕正垂轴旋转，可使其变换为水平线，第二次绕铅垂轴旋转，可使其变换为正垂线。
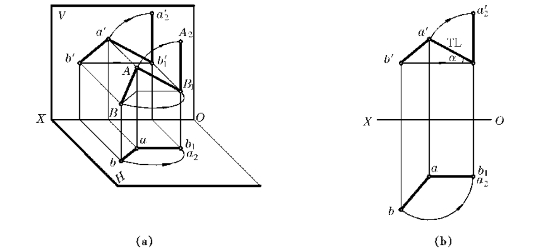
图4—17 一般线旋转为铅垂线
有关画法几何及土木工程制图（第4版）的文章
- 详细阅读
-
直线上的点-《画法几何及土木工程制图》详细阅读
如图2—15中直线AB上有一点K，通过K点作垂直于H面的投射线Kk，它必在通过AB的投射平面ABba内，故K点的H面投影k必在AB的投影ab上。2）定比性关系直线上的点将直线分为几段，各线段长度之比等于它们的同面投影长度之比。图2—15直线上的点的投影例2—5如图2—16a所示，已知ab和a′b′，求直线AB上K点的投影，使AK∶KB＝2∶3。边a′任作一直线，在其上量取：a′1＝am，a′2＝an，a′3＝ab。......
2023-09-24
-
直线标高投影：画法几何及土木工程制图详细阅读
1）直线的表示法在标高投影中，直线的位置是由直线上的两个点或直线上一点及该直线的方向确定。图9—4求线段的实长与倾角在实际工作中，常遇到直线两端的标高投影的高程并非整数，需要在直线的标高投影上作出各整数标高点。例9—2如图9—5所示，已知直线AB的标高投影a4.3b7.8，求直线上各整数标高点。解平行于直线AB作一辅助的铅垂面，采用标高投影比例尺作相应高程的水平线，最高一条为8，最低一条为4。......
2023-09-24
-
两直线相对位置-画法几何及土木工程制图详细阅读
两直线之间的基本相对位置有三种：平行、相交、交叉。图2—20两直线相交反之，若两直线的三组同面投影均相交，且交点符合点的投影规律，则空间两直线必相交。图2—21判别两直线是否相交解一般情况下，根据V和H两投影就可判定是否相交，但若两直线中有一条是侧平线，则需要作出W投影。所以在这里仅讨论两直线垂直相交时的投影特性，所得结论对于两直线垂直交叉时仍同样适用。......
2023-09-24
-
直线透视投影方法画法几何及土木工程制图详细阅读
1）直线的透视特性直线的透视及基透视，一般情况下仍是直线。迹点的透视即为其本身，其基透视则在基线上。直线的透视必通过直线的画面迹点，直线的基透视必通过该迹点在基面上的正投影。直线上离画面无穷远点的透视，称为直线的灭点，直线的透视延长后一定通过灭点。把直线的迹点和灭点相连可得直线的全长透视。......
2023-09-24
-
直线变换法则-画法几何及土木工程制图详细阅读
图4—5一般线变换为H1面平行线2）将投影面平行线变换为新投影面垂直线这时新投影面必须垂直于该直线，于是该直线的新投影有积聚性。图4—7正平线变换为H1垂直线3）将一般位置直线变换成新投影面垂直线综合上述两种变换的情况，可连续作两次换面，第一次将一般线变换为新投影面的平行线，第二次将其变换为新投影面的垂直线。图4—8一般线变换为投影面垂直线......
2023-09-24
-
各种位置直线-画法几何及土木工程制图详细阅读
为了详细研究直线的投影性质，可按直线与三个投影面的相对位置，将其分为三类：一般位置直线、投影面平行线、投影面垂直线。后两类统称为特殊位置直线。图2—10一般位置直线2）投影面平行线只平行于一个投影面，且倾斜于另外两个投影面的直线，称为投影面平行线。表2—2投影面垂直线例2—3如图2—11a所示，已知A点的两面投影，正平线AB＝20，且α＝30°，作出直线AB的三面投影。......
2023-09-24
-
棱柱体投影技巧-画法几何及土木工程制图详细阅读
画棱柱体的投影时，一般是使其侧棱线垂直于某投影面。如图6—1a所示，正五棱柱在三面投影体系中的位置：顶面和底面是水平面且为正五边形，五个侧棱面均为矩形，除后侧棱面是正平面外，其余均是铅垂面，五条侧棱线均是铅垂线。图6—1正五棱柱的投影在棱柱面上取点和线，可利用有积聚性的投影来作图。例6—1如图6—2a所示，已知五棱柱面上A点的V投影a′和CD线的V投影c′d′，求作它们的其他两投影。......
2023-09-24
相关推荐