如图2—15中直线AB上有一点K，通过K点作垂直于H面的投射线Kk，它必在通过AB的投射平面ABba内，故K点的H面投影k必在AB的投影ab上。2）定比性关系直线上的点将直线分为几段，各线段长度之比等于它们的同面投影长度之比。图2—15直线上的点的投影例2—5如图2—16a所示，已知ab和a′b′，求直线AB上K点的投影，使AK∶KB＝2∶3。边a′任作一直线，在其上量取：a′1＝am，a′2＝an，a′3＝ab。......
2023-09-24
直线变换法则-画法几何及土木工程制图
【摘要】：图4—5一般线变换为H1面平行线2）将投影面平行线变换为新投影面垂直线这时新投影面必须垂直于该直线，于是该直线的新投影有积聚性。图4—7正平线变换为H1垂直线3）将一般位置直线变换成新投影面垂直线综合上述两种变换的情况，可连续作两次换面，第一次将一般线变换为新投影面的平行线，第二次将其变换为新投影面的垂直线。图4—8一般线变换为投影面垂直线
直线的投影变换，只需求出其上两端点的新投影，然后相连即得到直线的新投影。
换面作图方法已经解决，这里关键是如何设立新投影面的位置，以使直线变换为特殊位置。而新投影面的设立归结为新投影轴的选择，因为在投影图中，新投影轴的位置就是新投影面的积聚投影。
直线的变换有三种基本情况，现分述如下：
1）将一般位置直线变换成新投影面平行线
为此，新投影面必须平行于该直线，于是该直线的新投影反映其实长和倾角。
如图4—4所示，AB是一般线，现用V1代换V面，令V1∥AB，且V1⊥H，于是O1X1∥ab。按点的换面规律作出A和B的新投影，连之即得AB的新投影a′1b′1，则有a′1b′1＝AB，a′1b′1与O1X1的夹角反映AB与H面的倾角α。
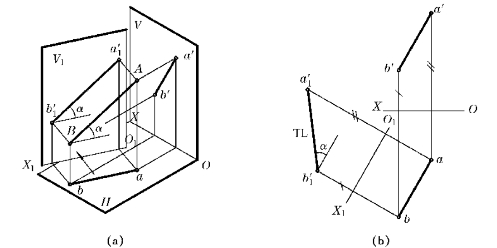
图4—4 一般线变换为V1面平行线
同理，若求一般线AB的实长和β角，应该用H1代换H面，令H1∥AB，且H1⊥V，于是O1X1∥a′b′，具体作图如图4—5所示。
图4—5 一般线变换为H1面平行线
2）将投影面平行线变换为新投影面垂直线
这时新投影面必须垂直于该直线，于是该直线的新投影有积聚性。
如图4—6所示，AB是水平线，现用V1代换V面，令V1⊥AB，且V1⊥H，于是O1X1⊥ab，作出AB的V1面投影，则a′1b′1积聚为一点。
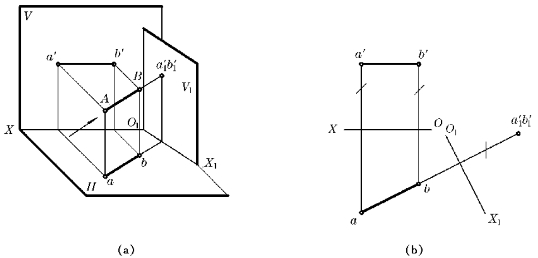
图4—6 水平线变换为V1垂直线
如图4—7所示，CD是正平线，用H1代换H面，令H1⊥CD，且H1⊥V，于是O1X1⊥c′d′，作出CD的H1面投影，则c1d1积聚为一点。
图4—7 正平线变换为H1垂直线
3）将一般位置直线变换成新投影面垂直线
综合上述两种变换的情况，可连续作两次换面，第一次将一般线变换为新投影面的平行线，第二次将其变换为新投影面的垂直线。
如图4—8所示，AB是一般线，第一次用V1代换V面，令V1∥AB，且V1⊥H，于是O1X1∥ab，作出a′1b′1，第二次用H2代换H，使H2⊥AB，且H2⊥V1，于是O2X2⊥a′1b′1，作出的a2b2积聚为一点。
同理，若第一次用H1代换H面，第二次用V2代换V面，则也能使AB在V2面上的投影积聚为一点。读者可按此变换次序自行作图。
图4—8 一般线变换为投影面垂直线
有关画法几何及土木工程制图（第4版）的文章
- 详细阅读
-
直线标高投影：画法几何及土木工程制图详细阅读
1）直线的表示法在标高投影中，直线的位置是由直线上的两个点或直线上一点及该直线的方向确定。图9—4求线段的实长与倾角在实际工作中，常遇到直线两端的标高投影的高程并非整数，需要在直线的标高投影上作出各整数标高点。例9—2如图9—5所示，已知直线AB的标高投影a4.3b7.8，求直线上各整数标高点。解平行于直线AB作一辅助的铅垂面，采用标高投影比例尺作相应高程的水平线，最高一条为8，最低一条为4。......
2023-09-24
-
两直线相对位置-画法几何及土木工程制图详细阅读
两直线之间的基本相对位置有三种：平行、相交、交叉。图2—20两直线相交反之，若两直线的三组同面投影均相交，且交点符合点的投影规律，则空间两直线必相交。图2—21判别两直线是否相交解一般情况下，根据V和H两投影就可判定是否相交，但若两直线中有一条是侧平线，则需要作出W投影。所以在这里仅讨论两直线垂直相交时的投影特性，所得结论对于两直线垂直交叉时仍同样适用。......
2023-09-24
-
直线透视投影方法画法几何及土木工程制图详细阅读
1）直线的透视特性直线的透视及基透视，一般情况下仍是直线。迹点的透视即为其本身，其基透视则在基线上。直线的透视必通过直线的画面迹点，直线的基透视必通过该迹点在基面上的正投影。直线上离画面无穷远点的透视，称为直线的灭点，直线的透视延长后一定通过灭点。把直线的迹点和灭点相连可得直线的全长透视。......
2023-09-24
-
各种位置直线-画法几何及土木工程制图详细阅读
为了详细研究直线的投影性质，可按直线与三个投影面的相对位置，将其分为三类：一般位置直线、投影面平行线、投影面垂直线。后两类统称为特殊位置直线。图2—10一般位置直线2）投影面平行线只平行于一个投影面，且倾斜于另外两个投影面的直线，称为投影面平行线。表2—2投影面垂直线例2—3如图2—11a所示，已知A点的两面投影，正平线AB＝20，且α＝30°，作出直线AB的三面投影。......
2023-09-24
-
直线旋转技巧-画法几何及土木工程制图详细阅读
由此，可总结出直线的旋转规律如下：图4—14直线的旋转若直线绕垂直于某投影面的轴旋转时，则其在该投影面上的投影长度不变，且其对该投影面的倾角亦不变。为了将直线旋转到有利于解题的特殊位置，选择旋转轴和旋转角度至关重要。图4—16正平线旋转为铅垂线3）将一般位置直线旋转成投影面垂直线综合上述两种旋转的情况，可以连续作两次旋转，第一次将一般线旋转为投影面平行线，第二次将其旋转成投影面垂直线。......
2023-09-24
-
投影变换解题举例书名：画法几何及土木工程制图详细阅读
根据换面法和旋转法的基本原理，可将一般位置的直线和平面变换到特殊位置，以达到解题的目的。由于本题中AB和CD均为一般线，不能直接作出公垂线的投影，若把其中任一直线变换为与投影面垂直时，可根据其积聚投影作出公垂线和距离，为此需要经过两次变换，现用换面法作图。......
2023-09-24
-
给水排水制图规定-画法几何及土木工程制图详细阅读
1）图线建筑给水排水制图采用的各种图线宜符合表16—1的规定。表16—2给水排水制图的比例在建筑给水排水轴测系统图中，如局部表示有困难时，该处可不按比例绘制。编号用分数形式表示，分子为管道类别代号，分母为管道进出口序号，标注方法见图16—11。建筑物内穿过楼层的立管，其数量多于一根时，宜用阿拉伯数字编号，表示形式为“管道类别和立管代号—编号”。表16—3给水排水制图常用图例......
2023-09-24
相关推荐