直线与平面平行的几何条件：若直线平行于平面内任一直线，则该直线与平面互相平行。所求水平线MN必须平行于△ABC内的水平线。例3—2如图3—3a所示，判断直线MN与平面ABCD是否平行。解问题归结于能否在ABCD内作出平行于MN的直线。如图3—3b所示，可先在ABCD内任作一直线EF，使e′f′∥m′n′，再求出ef。当平面处于特殊位置时，该平面的某个投影有积聚性，则平行关系可以从积聚性投影中反映出来。......
2023-09-24
直线与平面垂直的画法几何与土木工程制图
【摘要】：直线与平面垂直的几何条件：若直线垂直于平面内的两相交直线，则该直线与平面垂直。图3—18直线与平面垂直的投影特性例3—5如图3—19a所示，已知△ABC和M点，过M点作△ABC的垂线MN。如图3—21所示，正平线MN与正垂面P垂直。
直线与平面垂直的几何条件：若直线垂直于平面内的两相交直线，则该直线与平面垂直。反之，若直线与平面垂直，则该直线垂直于平面内的所有直线。如图3—17所示，由于MN⊥AB，MN⊥CD，且AB×CD，因此MN⊥P[AB×CD]。若已知MN⊥P，则MN与P平面内的所有直线均垂直，如图中MN⊥EF，MN⊥KL（两直线的垂直可以是相交垂直，也可以是交叉垂直）。
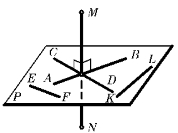
图3—17 直线与平面垂直的几何条件
根据上面的分析，直线与平面的垂直问题就转化成两直线的垂直问题。直线垂直于平面，必垂直于平面内的投影面平行线。如图3—18a所示，直线MN垂直于P平面，必垂直于P平面内的水平线AB和正平线AC。由直角投影定理可知，在投影图中mn⊥ab，m′n′⊥a′c′，如图3—18b所示。于是可得到直线与平面垂直的投影特性如下：
若直线垂直于平面，则该直线的H投影垂直于平面内水平线的H投影，该直线的V投影垂直于平面内正平线的V投影，该直线的W投影垂直于平面内侧平线的W投影。
根据直线与平面垂直的投影特性，可以作已知平面的垂线，或作已知直线的垂面，也可以判断直线与平面是否垂直。
图3—18 直线与平面垂直的投影特性
例3—5 如图3—19a所示，已知△ABC和M点，过M点作△ABC的垂线MN。
图3—19 作已知平面的垂线
解 作图步骤如图3—19b，c所示：
（1）作△ABC内的水平线AD[ad，a′d′]，再作mn⊥ad；
（2）作△ABC内的正平线CE[ce，c′e′]，再作m′n′⊥c′e′；
（3）于是所作MN⊥△ABC。
例3—6 如图3—20a所示，判断直线MN是否垂直于△ABC。
图3—20 判断直线与平面是否垂直
图3—21 正平线与正垂面垂直
解 看平面△ABC内的水平线和正平线是否与MN垂直，判断过程如图3—20b：
（1）作△ABC内的水平线AD[ad，a′d′]，因ad⊥mn，故AD⊥MN；
（2）作△ABC内的正平线CE[ce，c′e′]，因c′e′⊥\m′n′，故CE⊥\MN（⊥\为不垂直）；
（3）虽然MN⊥AD，但MN⊥\CE，所以MN⊥\△ABC。
在特殊情况下，当平面垂直于某投影面，而直线又平行于该投影面时，则在该投影面上的投影反映它们夹角的真实大小。如图3—21所示，正平线MN与正垂面P垂直。
有关画法几何及土木工程制图（第4版）的文章
- 详细阅读
-
直线上的点-《画法几何及土木工程制图》详细阅读
如图2—15中直线AB上有一点K，通过K点作垂直于H面的投射线Kk，它必在通过AB的投射平面ABba内，故K点的H面投影k必在AB的投影ab上。2）定比性关系直线上的点将直线分为几段，各线段长度之比等于它们的同面投影长度之比。图2—15直线上的点的投影例2—5如图2—16a所示，已知ab和a′b′，求直线AB上K点的投影，使AK∶KB＝2∶3。边a′任作一直线，在其上量取：a′1＝am，a′2＝an，a′3＝ab。......
2023-09-24
-
平面内的点和直线：画法几何及土木工程制图详细阅读
通常所说在平面内作点和直线，均是指所作的点和直线应属于该平面的空间位置。平面内的投影面平行线既应符合平面内直线的几何条件，又要符合投影面平行线的投影特性。平面内垂直于水平线的直线，称为对H面的最大坡度线；平面内垂直于正平线的直线，称为对V面的最大坡度线；平面内垂直于侧平线的直线，称为对W面的最大坡度线。在图2—36中，画出了P平面内的三种最大坡度线。......
2023-09-24
-
直线标高投影：画法几何及土木工程制图详细阅读
1）直线的表示法在标高投影中，直线的位置是由直线上的两个点或直线上一点及该直线的方向确定。图9—4求线段的实长与倾角在实际工作中，常遇到直线两端的标高投影的高程并非整数，需要在直线的标高投影上作出各整数标高点。例9—2如图9—5所示，已知直线AB的标高投影a4.3b7.8，求直线上各整数标高点。解平行于直线AB作一辅助的铅垂面，采用标高投影比例尺作相应高程的水平线，最高一条为8，最低一条为4。......
2023-09-24
-
画法几何及土木工程制图：路线平面图详细阅读
2）画法特点和表达内容路线平面图主要是表示路线的走向和平面线型状况，以及沿线两侧一定范围内的地形、地物等情况。如图19—1所示，为某公路从K3＋300至K5＋200段的路线平面图。在路线平面图上应画出指北针或测量坐标网，用来指明道路在该地区的方位与走向。在路线平面图中，转折处应注写交角点代号并依次编号，如JD6表示第6个交角点。图19—3路线平面图的拼接......
2023-09-24
-
平面旋转技巧-《画法几何及土木工程制图》详细阅读
为了将平面旋转到有利于解题的特殊位置，关键是确定旋转轴的位置和选择适当的旋转角度。2）将投影面垂直面旋转成投影面平行面以正垂线为旋转轴，可将正垂面旋转为水平面，其H投影反映实形。如图4—20所示，△ABC为正垂面，绕通过B点的正垂轴旋转，使其变换为水平面△A1BC1，于是△a1bc1≌△ABC。图4—21一般面旋转为水平面......
2023-09-24
- 详细阅读
-
两直线相对位置-画法几何及土木工程制图详细阅读
两直线之间的基本相对位置有三种：平行、相交、交叉。图2—20两直线相交反之，若两直线的三组同面投影均相交，且交点符合点的投影规律，则空间两直线必相交。图2—21判别两直线是否相交解一般情况下，根据V和H两投影就可判定是否相交，但若两直线中有一条是侧平线，则需要作出W投影。所以在这里仅讨论两直线垂直相交时的投影特性，所得结论对于两直线垂直交叉时仍同样适用。......
2023-09-24
相关推荐