1）一般位置直线与一般位置平面相交若直线和平面均处于一般位置时，它们的投影均无积聚性，因而不能直接作出交点，要作交点常采用辅助平面法。2）两一般位置平面相交求两个一般面的交线，可用前述直线与平面求交点的方法。如图3—16a所示为两一般面△ABC与△DEF相交。图3—16两一般面相交利用重影点分别判断两平面H和V投影的可见性。......
2023-09-24
特殊位置相交：画法几何与土木工程制图改进版
【摘要】：1）一般位置直线和特殊位置平面相交由于平面处于特殊位置时，某一投影有积聚性，因此可利用其积聚投影作出交点，并判别可见性。图3—12水平面与正垂面相交3）两特殊位置平面相交两平面均垂直于某投影面时，它们的交线也垂直于该投影面。如图3—13a所示，一般面△ABC与铅垂面P相交。由于P面的H投影积聚为p，交线KL的H投影kl重合在p上；KL又是△ABC内的直线，可由kl作出k′l′。
1）一般位置直线和特殊位置平面相交
由于平面处于特殊位置时，某一投影有积聚性，因此可利用其积聚投影作出交点，并判别可见性。如图3—10a所示，一般线MN与铅垂面P相交。交点K既在MN上又在P面内，现P面的H投影积聚为直线p，故mn与p的交点即为k，然后由k作投影连线，与m′n′相交于k′，K[k，k′]即为MN与P的交点，如图3—10b所示。
图3—10 一般线与铅垂面相交
在V投影中，m′n′与p′重影，根据H投影判断，KM段在P面之前是可见的，于是将k′m′画为实线，KN段在P面之后的一部分被遮住是不可见的，将k′n′画为虚线，如图3—10c所示。注意超出P面（矩形）范围之外的部分没有被遮住，仍应画为实线。
在H投影中，由于P面有积聚性，从上向下投射，km和kn两段均可见，故全画成实线。一般说来，平面的某投影积聚时，在该投影面的投影全为可见，不需另作判别。
2）投影面垂直线与一般位置平面相交
由于直线有积聚性，可利用积聚投影作出交点，再利用重影点判别可见性。
如图3—11a所示，正垂线MN与一般面△ABC相交。交点K是直线MN上的点，k′一定重合于其积聚投影m′n′，K点又在△ABC内，现已知k′，可根据平面上取点的方法作辅助线AE，然后求出k，如图3—11b所示。
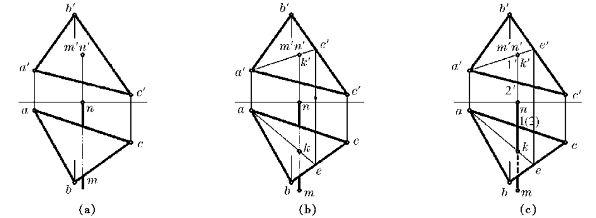
图3—11 正垂线与一般面相交
在H投影中，利用两交叉直线的重影点来判别可见性。例如mn和ac的交点1（2），是MN上Ⅰ点和AC上Ⅱ点的重影点，由V投影看出，Ⅰ点在上，Ⅱ点在下，故kn段是可见的，应画为实线，km段是不可见的，应将重叠部分画为虚线，如图3—11c所示。直线总是以交点为界，一段可见，另一段不可见，或者说交点是虚线和实线的分界点。
图3—12 水平面与正垂面相交
3）两特殊位置平面相交
两平面均垂直于某投影面时，它们的交线也垂直于该投影面。可利用两平面的积聚投影求交线，并判别可见性。
如图3—12a所示，水平面P与正垂面Q相交。由于P和Q均垂直于V面，故交线KL必为正垂线。V投影p′和q′的交点即为k′l′，然后作出交线的H投影，kl的长度应根据p和q的重叠部分来确定，如图3—12b所示。
根据平面的积聚性投影可知，以交线为界，左侧是P面在上为可见，Q面在下为不可见，而右侧正相反。于是在H投影中，在交线kl的左侧将P面（三角形）的轮廓线画成实线，将Q面（矩形）的重叠部分的轮廓线画为虚线。在交线kl的右侧，两平面的虚线和实线与左侧正相反，最后结果如图3—12c所示。
4）一般位置平面与特殊位置平面相交
利用特殊位置平面的积聚投影求交线并判别可见性。
如图3—13a所示，一般面△ABC与铅垂面P相交。由于P面的H投影积聚为p，交线KL的H投影kl重合在p上；KL又是△ABC内的直线，可由kl作出k′l′。作图时，可分别作出AB，AC与P面的交点K[k，k′]和L[l，l′]，连之即得交线KL，见图3—13b。
根据H投影可判断出△ABC的AKL部分在P面之前，故在V投影中a′k′l′是可见的，另一部分不可见，虚线和实线如图3—13c所示。
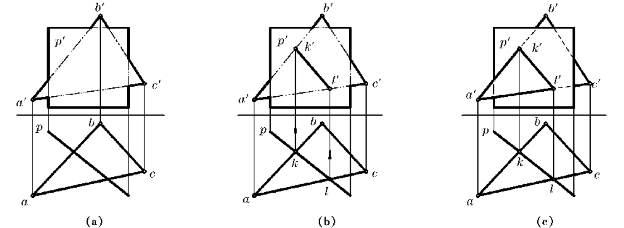
图3—13 铅垂面与一般面相交
有关画法几何及土木工程制图（第4版）的文章
- 详细阅读
-
各种位置直线-画法几何及土木工程制图详细阅读
为了详细研究直线的投影性质，可按直线与三个投影面的相对位置，将其分为三类：一般位置直线、投影面平行线、投影面垂直线。后两类统称为特殊位置直线。图2—10一般位置直线2）投影面平行线只平行于一个投影面，且倾斜于另外两个投影面的直线，称为投影面平行线。表2—2投影面垂直线例2—3如图2—11a所示，已知A点的两面投影，正平线AB＝20，且α＝30°，作出直线AB的三面投影。......
2023-09-24
-
两直线相对位置-画法几何及土木工程制图详细阅读
两直线之间的基本相对位置有三种：平行、相交、交叉。图2—20两直线相交反之，若两直线的三组同面投影均相交，且交点符合点的投影规律，则空间两直线必相交。图2—21判别两直线是否相交解一般情况下，根据V和H两投影就可判定是否相交，但若两直线中有一条是侧平线，则需要作出W投影。所以在这里仅讨论两直线垂直相交时的投影特性，所得结论对于两直线垂直交叉时仍同样适用。......
2023-09-24
-
两平面体的相交线-画法几何及土木工程制图详细阅读
两平面体的相贯线一般情况下为空间折线，特殊情况下可为平面折线。交线法——直接作出两平面体上两个相应棱面的交线，然后组成相贯线。因此，求两平面体的相贯线，实质上就归结为求直线与平面的交点和两平面的交线。例6—12如图6—17a所示，求作两三棱柱ABC和DEF的相贯线。图6—17作两三棱柱的相贯线（全贯）作图过程如图6—17b所示：作出各棱线的交点。......
2023-09-24
-
两点相对位置-画法几何及土木工程制图详细阅读
两个点在空间的相对位置关系，是以其中一个点为基准，来判定另一点在该点的左或右、前或后、上或下。反之如果已知两点的相对位置，以及其中一点的投影，也可以依照上述原理作出另一点的投影。图2—8两点的相对位置如图2—9a所示，A点和B点在同一条垂直于H面的投射线上，它们的H投影a和b重合。图2—9重影点的位置及其可见性......
2023-09-24
-
给水排水制图规定-画法几何及土木工程制图详细阅读
1）图线建筑给水排水制图采用的各种图线宜符合表16—1的规定。表16—2给水排水制图的比例在建筑给水排水轴测系统图中，如局部表示有困难时，该处可不按比例绘制。编号用分数形式表示，分子为管道类别代号，分母为管道进出口序号，标注方法见图16—11。建筑物内穿过楼层的立管，其数量多于一根时，宜用阿拉伯数字编号，表示形式为“管道类别和立管代号—编号”。表16—3给水排水制图常用图例......
2023-09-24
-
一般位置直线的实长与倾角|画法几何及土木工程详细阅读
一般线对三个投影面都是倾斜的，因而三个投影均不能直接反映直线的实长和倾角，但可根据直线的投影用作图的方法求出其实长和倾角。如果能作出该直角三角形△ABA1，便可以求得直线AB的实长和α角。利用直角三角形求一般线的实长和倾角的方法，称为直角三角形法。切记上面所述的三个直角三角形是完全不同的，虽然它们的斜边均为直线的实长，但反映出的倾角却不一样。......
2023-09-24
-
外墙剖面节点详图-画法几何土木工程制图详细阅读
外墙剖面节点的位置明显，一般不需要标注剖切位置。外墙剖面节点图通常采用1∶10或1∶20的比例绘制。图14—18培训楼外墙剖面节点详图图14—18是培训楼A轴线处外墙剖面节点详图。详图①是屋顶外墙剖面节点，它表明屋面、女儿墙及窗过梁之间的关系和做法。外墙从上至下有许多节点，但基本上只有这三种节点类型，故而一般只需画出这三处详图作为通用图。......
2023-09-24
相关推荐