图2-52平面上的直线的投影规律2.5.3.2平面内与投影面平行的直线凡在平面内平行于某一投影面的直线，称为投影面的平行线，可分为以下三种情况。平面上与投影面倾角最大的直线称为最大斜度线。......
2025-09-29
平面内的点和直线：画法几何及土木工程制图
【摘要】：通常所说在平面内作点和直线，均是指所作的点和直线应属于该平面的空间位置。平面内的投影面平行线既应符合平面内直线的几何条件，又要符合投影面平行线的投影特性。平面内垂直于水平线的直线，称为对H面的最大坡度线；平面内垂直于正平线的直线，称为对V面的最大坡度线；平面内垂直于侧平线的直线，称为对W面的最大坡度线。在图2—36中，画出了P平面内的三种最大坡度线。
根据平面的投影就可以确定该平面在空间位置。通常所说在平面内（或平面上）作点和直线，均是指所作的点和直线应属于该平面的空间位置。
1）点和直线在平面内的几何条件
图2—31 平面内的点和直线
（1）若点在平面内的一条已知直线上，则该点在平面内。
（2）若直线通过平面内的两个已知点；或通过平面内的一个已知点，且平行于平面内的另一条已知直线，则该直线在平面内。
例如图2—31所示：K点在已知直线BC上，故K点在平面ABC内；M，N是平面ABC内的两个已知点，因此直线MN在平面内；由于A点是平面内的已知点，且AD∥BC，所以直线AD在平面ABC内。
根据以上几何条件，不仅可以在平面内取点和直线，而且可以根据它们的投影判断点和直线是否在平面内。
例2—11 如图2—32a所示，已知平面△ABC[△abc，△a′b′c′]和点D[d，d′]，判断D点是否在平面ABC内。
解 如果D点在平面ABC内的一条直线上，则D点在平面内，否则就不在。作图步骤如图2—32b所示：
（1）在H投影中，过d任作一辅助直线ad，ad交bc于e；
（2）作出平面ABC内的辅助直线AE的V投影a′e′；
（3）由于d′不在该辅助直线a′e′上，故D点不在平面ABC内。
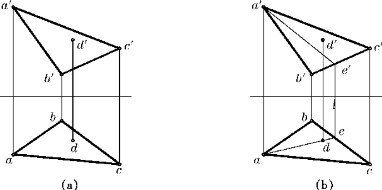
图2—32 判断点是否在平面内
图2—33 平面内的投影面平行线
2）平面内的投影面平行线
平面内的投影面平行线有三种，即平面内的水平线、正平线、侧平线。如图2—33所示，在平面P内画出了这三种直线，每种直线均互相平行，且与相应的迹线平行，如水平线与PH平行，正平线与PV平行，侧平线与PW平行。
平面内的投影面平行线既应符合平面内直线的几何条件，又要符合投影面平行线的投影特性。
如图2—34所示，在△ABC平面内分别作出了水平线AD、正平线CE、侧平面BF。
图2—34 作平面内的水平线、正平线、侧平线(https://www.chuimin.cn)
例2—12 在△ABC平面内求作M点，使M点距H面为10，距V面为15（图2—35）。
解 在△ABC平面内作出距H面为10mm的水平线DE，再作出距V面为15mm的正平线FG，两条线的交点M必满足要求。作图步骤如下：
（1）先作d′e′∥OX，且距OX为10，再作出de，如图2—35a所示；
（2）作fg∥OX，且距OX为15，fg与de相交于m，如图2—35b所示；
（3）由m作出d′e′上的m′，点M[m，m′]即为所求，如图2—35c所示。
图2—35 求平面内的M点
3）平面的最大坡度线
平面内对投影面倾角为最大的直线，称为平面的最大坡度线（或称最大斜度线），它垂直于平面内相应的投影面平行线。平面内垂直于水平线的直线，称为对H面的最大坡度线；平面内垂直于正平线的直线，称为对V面的最大坡度线；平面内垂直于侧平线的直线，称为对W面的最大坡度线。在图2—36中，画出了P平面内的三种最大坡度线。
图2—36 平面内的三种最大坡度线
图2—37 对H面的最大坡度线
图2—37中AD是P平面的对H面的最大坡度线，它垂直于迹线PH，PH可看作P平面内的一条水平线。现证明在P平面内的所有直线中，AD的α角最大：在P平面内过A点任作一直线AE，它对H面的倾角为α1，在直角△ADa中有
，在直角△AEa中有
，又△AED为直角三角形，故AD＜AE，所以α＞α1。
由图2—37还可以看出，平面P对H面的最大坡度线AD的α角，就反映了该平面的α角。同理可知，对V面的最大坡度线的β角，反映该平面的β角；对W面的最大坡度线的γ角，反映该平面的γ角。因此欲求一般位置平面的倾角，可利用该平面的最大坡度线来作图求解。
例2—13 求△ABC的倾角α（图2—38）。
解 作图步骤：
（1）作平面内的水平线AD[ad，a′d′]，如图2—38a所示；
（2）作平面内的直线BE⊥AD，BE[be，b′e′]即为对H面的最大坡度线，如图2—38b所示；
（3）用直角三角形法求出BE的α角，即为平面△ABC的α角，如图2—38c所示。
图2—38 求一般面的α角
相关文章
- 详细阅读
-
各种位置直线-画法几何及土木工程制图详细阅读
为了详细研究直线的投影性质，可按直线与三个投影面的相对位置，将其分为三类：一般位置直线、投影面平行线、投影面垂直线。后两类统称为特殊位置直线。图2—10一般位置直线2）投影面平行线只平行于一个投影面，且倾斜于另外两个投影面的直线，称为投影面平行线。表2—2投影面垂直线例2—3如图2—11a所示，已知A点的两面投影，正平线AB＝20，且α＝30°，作出直线AB的三面投影。......
2025-09-30
-
平面表示方法-画法几何及土木工程制图详细阅读
1）几何元素表示平面由几何公理可知，在空间不属于同一直线上的三点确定一平面。2）迹线表示平面平面与投影面的交线称为迹线。如图2—28所示，P平面与H面、V面、W面的交线分别称为水平迹线PH、正面迹线PV、侧面迹线PW。迹线是投影面内的直线，它的一个投影就是其本身，另两个投影与投影轴重合，用迹线表示平面时，是用迹线本身的投影来表示的。任意两条迹线都可以确定平面的空间位置，实质上就是两相交直线表示平面的特例。......
2025-09-30
-
两直线相对位置-画法几何及土木工程制图详细阅读
两直线之间的基本相对位置有三种：平行、相交、交叉。图2—20两直线相交反之，若两直线的三组同面投影均相交，且交点符合点的投影规律，则空间两直线必相交。图2—21判别两直线是否相交解一般情况下，根据V和H两投影就可判定是否相交，但若两直线中有一条是侧平线，则需要作出W投影。所以在这里仅讨论两直线垂直相交时的投影特性，所得结论对于两直线垂直交叉时仍同样适用。......
2025-09-30
-
点、直线、平面的投影简介详细阅读
2-19一等腰直角△ABC，AC为斜边，顶点B在直线NC上，完成其两面投影。2-20已知菱形ABCD的对角线BD的投影和另一对角线端点的水平面投影a，试完成菱形的投影图。2-25完成下列平面图形的第三投影，并求作出属于平面上的点K的另两个投影，并填空。2-26作图判断点A或直线AB是否属于给定的平面。2-34过已知点A作一直线AB，使其平行于已知平面△DEF。2-36求作直线与平面的交点K，并判断可见性。......
2025-09-29
-
两点相对位置-画法几何及土木工程制图详细阅读
两个点在空间的相对位置关系，是以其中一个点为基准，来判定另一点在该点的左或右、前或后、上或下。反之如果已知两点的相对位置，以及其中一点的投影，也可以依照上述原理作出另一点的投影。图2—8两点的相对位置如图2—9a所示，A点和B点在同一条垂直于H面的投射线上，它们的H投影a和b重合。图2—9重影点的位置及其可见性......
2025-09-30
-
一般位置直线的实长与倾角|画法几何及土木工程详细阅读
一般线对三个投影面都是倾斜的，因而三个投影均不能直接反映直线的实长和倾角，但可根据直线的投影用作图的方法求出其实长和倾角。如果能作出该直角三角形△ABA1，便可以求得直线AB的实长和α角。利用直角三角形求一般线的实长和倾角的方法，称为直角三角形法。切记上面所述的三个直角三角形是完全不同的，虽然它们的斜边均为直线的实长，但反映出的倾角却不一样。......
2025-09-30
-
点、直线、平面的正投影特点详细阅读
图2-9正投影的类似性2.2.1.4重合性两个或两个以上的点、线、面具有同一投影时，称为重合，这种投影性质称为正投影的重合性，如图2-10所示。......
2025-09-29
相关推荐