在重力作用下,岩土中能够保持住的水,主要是结合水和部分孔隙毛细水或悬挂毛细水。表1-1松散岩土持水度数值表2.给水性给水性是指饱水岩土在重力作用下,能自由给出一定水量的性能。例如,当水位下降1m时,在重力作用下,1m2水平面积的岩土柱体释放出的水的体积为0.1m3,μ==0.1,则其给水度为0.1或10%。不同的岩土具有不同的透水性。对岩土透水性起决定性作用的是空隙的大小,其次才是空隙的多少。......
2025-09-30
2.7.2.1 灵敏度分析
在模拟一个含水层系统时,研究人员必须确定出容许偏差,在不明显影响模拟结果条件下,实际系统的参数可以不同。这些容许偏差常常是根据引入系统中参数的变动和观察系统特征的变化来确定。而应用灵敏度分析可更有效地确定这些容许偏差。
在承压含水层中,根据泰斯公式,有
![]()
式中
![]()
所以对于一个含水层模型的解,可写成如下形式:
h=h(x,y,t;T,μ*,Q)
式中,h表示水头,m。
当考虑其中一个参数变化,例如,把T看作是变量,当T有一个增量ΔT时,则
h*=h*(x,y,t;T+ΔT,μ*,Q)
假设该含水层模型的解在解析上取决于参数T和μ*;而T,μ*和Q均为自变量,则函数h*(x,t,t;T+ΔT,μ*,Q)可展开成泰勒级数,如果ΔT值很小,则第二项和高次项可忽略不计。
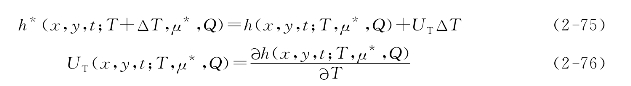
对于导水系数灵敏度UT(x,y,t;T,μ*,Q),以下均用UT表示。
如果灵敏度UT和原始水头已知,则由于导水系数的改变量ΔT而产生的新水头可由式(2-75)计算。
同理,如果贮水系统μ*的改变量Δμ*,则变动的新水头可由下式得出:
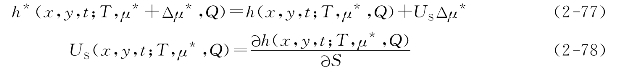
对于贮水系数灵敏度以US(x,y,t;T,μ*,Q),以下均用Us表示。
式(2-76)和式(2-78)表明,对于一个给定的模型,需要计算出UT和US。而对于各种变动下模型的反映,可以简单地从式(2-75)和式(2-77)简便地求出,而无须重新计算模型方程。
应用式(2-76)和式(2-78)所给的定义,可以从泰斯公式中求得灵敏度系数:(https://www.chuimin.cn)

如果μ*和T分别随Δμ*和ΔT的变化而变化,那么,从式(2-78)和式(2-80)中求出的UT和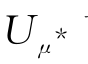 可用在式(2-75)和式(2-77)中求出降深值。有资料表明,当Δμ*和ΔT分别小于或等于μ*和T的20%时,式(2-75)和式(2-77)有效。
可用在式(2-75)和式(2-77)中求出降深值。有资料表明,当Δμ*和ΔT分别小于或等于μ*和T的20%时,式(2-75)和式(2-77)有效。
2.7.2.2 最小二乘法拟合
利用灵敏度分析的目的,是为了求得实际的抽水试验资料对泰斯方程的最小二乘法拟合,从而求得μ*和T的最佳值。
用ΔT和Δμ*改变的T和μ*后,新的降深值s*可按下式计算:
s*=s+UTΔT+USΔμ* (2-81)
令sc(t)表示t时刻测得的实际降深。假设对μ*和T能作出适当的估计,则s(t)为用这些参数从泰斯公式中算出的降深。对于μ和T的初步估计值,可用Δμ*和ΔT使之改变,应用式(2-81)计算新的降深值s*,借助于下列误差函数减至最小,得到与实际抽水试验资料拟合得更好的结果:
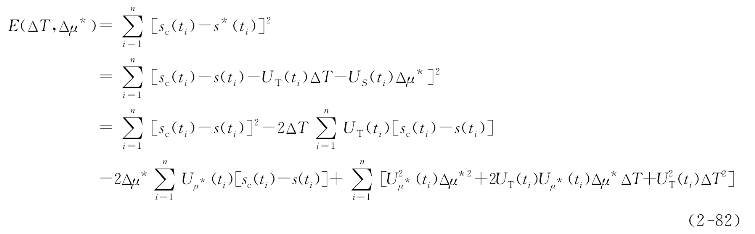
ti表示任意时刻,在该时刻可取得一个降深的试验值。误差函数由所有实测值sc与s*之差的平方和来确定,必须注意灵敏度系数UT和Uμ*取决于ti。
取ΔT和Δμ*的一阶导数并使其导数等于零,则误差为最小值,并解出ΔT,Δμ*的方程:
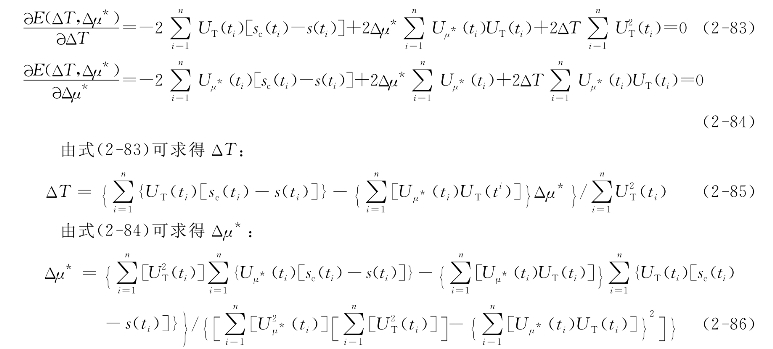
从式(2-86)中可求得Δμ*的最佳值(即最佳拟合结果)。将Δμ*值代入式(2-85)中,可找出ΔT的最佳拟合值。
ΔT和Δμ*的值可以用来校正T和μ*的第一次估算值。这个被改进后的T和μ*值,又重新被用在最小二乘法程序中,以便求得ΔT和Δμ*的新值,如此继续进行,直至ΔT和Δμ*小至可忽略不计时,迭代终止。第j次迭代后的最佳值,可用下列方程求得:

应用灵敏度分析方法计算含水层水文地质参数程序框图如图2-43所示。

图2-43 灵敏度分析方法计算含水层水文地质参数程序框图
如果T和μ*的初始值特别差,程序可能不会收敛。已有资料表明,即使对于μ*或T的初始值小于或大于两个数量级的情况下,也可获得好的收敛。
由上述可知,应用灵敏度分析、从最小二乘法判断中求得最佳的导水系数和贮水系数,从而使实际的抽水试验资料自动拟合泰斯公式,该法也可在更复杂的水文地质条件下应用。
相关文章

在重力作用下,岩土中能够保持住的水,主要是结合水和部分孔隙毛细水或悬挂毛细水。表1-1松散岩土持水度数值表2.给水性给水性是指饱水岩土在重力作用下,能自由给出一定水量的性能。例如,当水位下降1m时,在重力作用下,1m2水平面积的岩土柱体释放出的水的体积为0.1m3,μ==0.1,则其给水度为0.1或10%。不同的岩土具有不同的透水性。对岩土透水性起决定性作用的是空隙的大小,其次才是空隙的多少。......
2025-09-30

Kf是考虑交变电流趋肤效应和邻近效应对电阻的影响而引入的系数,即当导体中通过交变电流时,因趋肤效应和邻近效应而产生的附加损耗。则电阻损耗为式中:γ——材料的密度; m——材料的质量。电阻率ρ是温度θ的函数,其表达式为式中:ρ0、ρ20——0℃、200℃时的电阻率(Ω·m); α、β——电阻温度系数。......
2025-09-29

图4-9 风电机组的三维系数矩阵3)z轴为风速。取风速间隔为1m/s,根据风电机组的切入风速和切除风速的变化范围,把风速分为若干个区间。系数矩阵内每个元素CI是风电机组的风速系数。风速系数是以风电场输入风速为基准的,能反映场内每台风力机输入风速偏离风速基准值的大小,其计算框图如图4-10所示。以风电场输入风速为基准值,通过选择步长vstep、设定风速范围进行迭代计算,就可确定每台风电机组的风速系数。......
2025-09-29

漏磁通的多少表明了两个线圈之间耦合的紧密程度。图6.3表示了绕向和同名端的关系。图6.3两线圈绕向与同名端的关系检验学习结果6.1.1 写出图6.1和图6.2中线圈2两端的互感电压u2。......
2025-09-29

另一种是折算为E601蒸发量的折算系数,即式中:RE601为折算为E601蒸发量的折算系数。我国北方冬季(冰期)水面蒸发量,一般采用Φ20型蒸发器进行观测,它与E601的折算关系一般为0.5~0.65。而E601的折算系数,据辽宁省有20m2蒸发池与E6013a对比观测的结果是RE601=1.02,0.97,1.00平均为1.00,即E601在冰期的实测蒸发量即代表大水体的蒸发量,而用Φ20型的折算系数见表13.5。......
2025-09-30

梯级链是自动扶梯最重要的驱动部件,各部件应按无限疲劳寿命进行设计,因此其安全系数最小为5。重载型扶梯一般要求采用安全系数为8的梯级链。梯级链受力计算 梯级链的受力通常需考虑乘客的载荷、梯级链的张紧力及梯级和梯级链自重等,下面介绍一种计算方法。梯级链的使用寿命主要取决于销轴比压,该计算以自动扶梯的制动载荷进行校核。......
2025-09-29

能源消费弹性系数表示一个国家或地区某一年度能源消费增长率与经济增长率之比。一次能源消费弹性系数,一般简称为能源消费弹性系数。换言之,能源消费弹性系数是指一次能源消费增长与经济增长的关系,一次能源的范围仅限于商品能源。例如电力与经济增长的关系应选择与能源消费弹性系数相同的指标,电力与工业生产的关系应选择工业总产值指标等。能源消费弹性系数也适合于分析某一部门、行业或某一地区能源消费与经济增长的关系。......
2025-09-29
相关推荐