相对丰富的水源也决定了金塘岛有比较丰富的地下水，这使得水井众多。魏家老屋是一幢2层木结构四檐屋的北厢部分，据屋主魏永利介绍，这幢四檐屋是金塘山开禁以来的第一套大户宅院，说明魏氏最早入住中弄村。而魏家井可以说是金塘展复后魏家人在此拓荒定居打下的生存之井。虽历经重修，仍不失为金塘第一井。......
2023-10-15
根据多次流量试验估算抽水井导水系数和井损常数
【摘要】：通常，在利用抽水井获得的抽水资料来估算含水层参数时，由于未考虑井损因素，故直接影响求参的结果。这里介绍一种考虑了井损因素的估算导水系数和井损常数的方法。由上述可知，含水层的导水系数和井损常数可用若干不同流量的、每一次都是在抽水井中短时间的抽水得到的水位降深读数来估算。图2-42sg／Q-Q曲线计算导水系数T计算井损系数C
通常，在利用抽水井获得的抽水资料来估算含水层参数时，由于未考虑井损因素，故直接影响求参的结果。
这里介绍一种考虑了井损因素的估算导水系数和井损常数的方法。
2.7.1.1 基本原理
对承压含水层，泰斯公式的雅可布近似公式为
式（2-68）中的水位下降值s仅仅归因于含水层的性质。故将此方程直接用于抽水井测得的s数据是不适宜的。抽水井中测得的水位下降值至少包括两个主要部分：一是影响漏斗内含水层的特性造成的水位降；二是主要由于流入井内紊流造成的井损失。后者很难估计，而且每个井都不同。
井损失部分可近似地由下式计算：
式中 s′w——井损失部分形成的水位降深值，m；
C——井损系数，d2／m5；
Q——抽水量，m3／d。
因此，从方程（2-68）和方程（2-69），对时间t抽水井内的水位总下降值sg应为
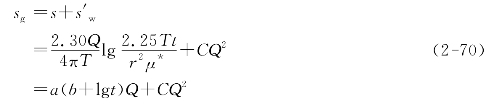
式中
如果一个井用不同的流量Q1，Q2，…，Qn进行n次抽水，而两次试验之间水位充分恢复，则对每一次抽水流量在相同时间t的总水位降可用一般式表示：
式中 A=a（b+lgtj）；
sgj——第j时刻抽水井中的总水位降深，m；
tj——第j时刻，j=1，2，…，m。
式（2-71）为一直线方程式。即如果在sg／Q-Q的曲线上，点绘在相同时刻、各次抽水的sgj／Qj与Qj的点，则得一直线，该直线与sg／Q轴的截距为A，斜率为C。同样，可以绘出若干条直线，每条直线的时间是不同的。所有的线都应该有相同的斜率C，但在sg／Q轴上的截距应不相同，如图2-41所示的t1，t2，…，tm直线。
设对相应时间t1，t2，…，tm的直线截距分别为A1，A2，…，Am，则
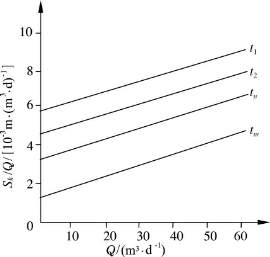
图2-41 多次流量试验分析图
式中，j=1，2，…，m。
所以
从式（2-71）和式（2-72）分别可得井损系数C和导水系数T。
由式（2-70）可得贮水系数μ＊：
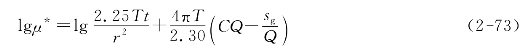
如果“r”被“rw”替代，井的有效半径rc将等于或大于井的实际半径rw，则方程式（2-73）变为
式（2-74）可以用于估算贮水系数的范围，只要将试验中的任一实际的水位降sg以及相应的Q和t代入式（2-74）即可。
2.7.1.2 应用步骤
1.试验方法
（1）以定流量Q1连续抽水到某一段时间（例如，20～30min足够）；
（2）最好用连续记录装置对抽水井测定水位降（例如，t=1，2，3，4，5，7，10，15，20，25，30min）；
（3）停止抽水，至水位充分恢复；
（4）分别以不同的抽水量Q2，…，Qn抽水，重复（1）至（3）的程序直至试验全部完成。
2.分析
（1）对应于不同t1，t2，…，tm不同的出水量Q1，Q2，…，Qn估算出水位降；
（2）对每一相应的时间计算出sg／Q；
（3）对每一t值计算方程式（2-71）的常数A和C；
（4）对不同的t值选择一对A值，其C值最密切符合；
（5）将这些A和t值代入方程式（2-72），计算导水系数；
（6）用方程式（2-74）计算贮水系数范围。
由上述可知，含水层的导水系数和井损常数可用若干不同流量的、每一次都是在抽水井中短时间的抽水得到的水位降深读数来估算。上述讨论适用于各种含水层的限制条件。实际上大多数野外条件适于此法的应用范围，主要因为时间t值和井的有效半径rc值都小。
考虑到实际上所打的每一个生产井不常有观测孔，因此，应用该法可以较简便地估算含水层的水文地质参数和井损系数。
2.7.1.3 工程实例
水文地质条件同本书“2.5.3工程实例”，多次抽水试验资料如表2-28和表2-29所示。
表2-28 多次抽水各时刻的降深值s m
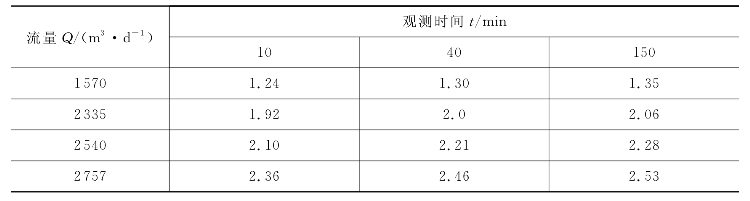
表2-29 多次抽水各时刻的sg／Q
（1）分别对t=10min，40min，150min绘制sg／Q-Q曲线，如图2-42所示的曲线①，②，③所示。
图2-42 sg／Q-Q曲线
（2）计算导水系数T
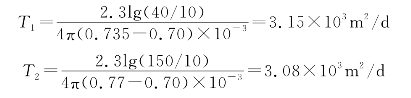
（3）计算井损系数C
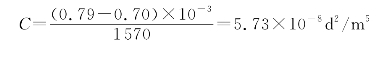
有关工程地下水（第2版）的文章
- 详细阅读
-
工程地下水：计算承压含水层的导水系数、贮水系详细阅读
它标志含水层在加压下的贮水的能力，或在减压下的释放水的能力。利用非稳定流抽水试验资料，可以计算导水系数T，贮水系数μ＊和压力传导系数a。图2-36s-lg曲线含水层水文地质参数汇总见表2-25。......
2023-09-23
-
水资源评价：13.4.4产流量估算详细阅读
13.4.4.3高原湖区产流量估算高原湖泊，如云南的滇池，一般是亏水的，即湖面的降水量小于湖面的蒸发量，湖泊本身要消耗其上游的来水。......
2023-08-23
-
东沙的井：井文化与舟山水井的历史详细阅读
作为有着文化礼仪之乡之称的东沙，公用水井、公用池潭在1795年之后开始走进东沙百姓的生活。因当时东沙人数较少，所以能勉强解决该地居民的饮用水问题。修好后，东沙社区立碑刻4条公告，算是使用义井的村规民约。戊辰河 位于东沙小学旁边，是个方方正正的“大井”，历史上又称食水河。尽管两河开通，还是满足不了东沙日益增多的人口用水需要。......
2023-10-15
-
宜昌汛期的日流量统计特征及估算方法详细阅读
例如在宜昌5～10月的汛期内日流量随机过程，每年有一次实现。，tn）为随机过程的n维概率密度函数，则n维分布函数为式可用以描述宜昌汛期180天日流量序列的全部统计特征。这样既能表征洪水过程的基本特征又能满足实际需要。在一般情况下，宜昌洪水随机过程为非平稳、非线性随机过程，但若提取确定性成分后，剩余序列通常近乎平稳随机过程。因而只需从一个样本函数即可估计平稳随机过程的统计特征。......
2023-08-23
-
工程地下水（第2版）中用灵敏度分析法计算导水详细阅读
图2-43灵敏度分析方法计算含水层水文地质参数程序框图如果T和μ＊的初始值特别差，程序可能不会收敛。由上述可知，应用灵敏度分析、从最小二乘法判断中求得最佳的导水系数和贮水系数，从而使实际的抽水试验资料自动拟合泰斯公式，该法也可在更复杂的水文地质条件下应用。......
2023-09-23
-
登步岛的井与井文化：探索舟山的水井遗产详细阅读
现登步岛主要有永安、鸡冠、大岙、蛏子港等数个村落，老井也主要集中在这些村落的居民集聚点，其中不少水井与登步岛的民俗民风、生产习俗有关，也留下了不少民间传说。水池登 又称大水池，位于登步岛鸡冠村。登步管委会近年来对大水池进行了整修美化，建成村民休闲游乐的小公园。附近有登步大岙文化墙，介绍大岙村史村貌、登步岛“五色文化”等。......
2023-10-15
-
舟山井文化：水井建设中的政府作为详细阅读
在舟山开凿一口水井的费用非常昂贵，民间独立开凿困难重重，因此不同于内陆地区以民间力量为主的水井建设方式，舟山的水井建设，必须要有政府部门的大力支持。所以对舟山而言，水井不仅是生活用水的提供源，还是海岛建设的必备要素。根据舟山水利部门的调查统计，至今舟山全市共有各类坑道井600余座，其数量甚至要多于普通水井。舟山水井和井文化建设的政府行为永无止境。目前舟山的文物部门发挥了重要的作用。......
2023-10-15
相关推荐