图2-8 复合沙山地形下的路线线形如果路基高度、边坡及和风向夹角等处理不当，就会对公路造成很大的危害，给养护带来困难。沙漠公路线形应在满足车辆行驶力学、美学及工程造价等要求的同时，顺应风沙流运动规律，和不同类型的沙漠地貌进行很好的环境景观配合，最后结合防沙体系，保证公路畅通。1）平曲线设计原则保持线形简捷连续，线形应与沙漠地形地貌相适应，与周边环境相协调。......
2023-09-22
风积沙路基公路设计、施工与防沙：压缩特性
【摘要】：对于风积沙来讲，其排水性良好，排水固结变形所需时间很短。因此，风积沙的压缩变形随时间的变化主要是由于一定压力作用下的颗粒骨架蠕变引起的。表1-37、图1-17表示压缩模量与压力的关系。试样竖向压缩应变ε与压力P的函数关系如下：ε＝0.004 594P 1／3R＝0.999随着压力P的增大，压缩模量E s愈来愈大；与黏性土相比，沙体的压缩模量较大，说明沙体的压缩性较差。
土是由固体颗粒、土中水和土中气体组成的三相体。与总的体积变形相比，土的颗粒变形非常小，一般可忽略不计；土中水也不可能产生压缩变形。因此，土的压缩变形是由土中空气体积的压缩和土中水的排出导致的。对于风积沙来讲，其排水性良好，排水固结变形所需时间很短。因此，风积沙的压缩变形随时间的变化主要是由于一定压力作用下的颗粒骨架蠕变引起的。
压缩试验按照JTGE 40《公路土工试验规程》的单轴排水固结法进行。试样通过铜模静压得到。
（1）试验设备：固结仪。
（2）荷载等级：50 kPa、100 kPa、300 kPa、400 kPa。
（3）含水量：2%。
（4）采样时间：0、0.25 min、1 min、2 min、5 min、10 min、30 min、1 h、2 h、4 h、8 h、24 h。
1）试样压缩量随时间的变化
表1-35和图1-15为沙样1的干密度为1.64 g／cm3时、在50 kPa的荷载作用下的压缩量随时间的变化。
表1-35 压缩量随时间变化关系
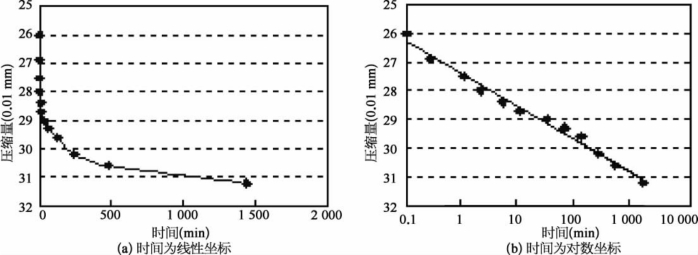
图1-15 压缩量随时间变化曲线
从图1-15a可以看出：
（1）在压力的作用下，沙体发生压缩变形，开始时变形速度较快，随后变形速度越来越慢，这说明砂性土也存在着对时间的滞后效应。
（2）如果将时间坐标由线性变为对数坐标，则可以得到图1-15b，从图可以看出，原来的曲线变为一条直线，而且相关性很好，函数关系如下：
Δh＝0.504 4ln t＋27.444R＝0.993 7
式中 Δh——压缩量（0.01 mm）；
t——时间（min）。
2）压缩量随压力的变化
表1-36为沙样1的干密度为1.64 g／cm3时在50 kPa、100 kPa、300 kPa、400 kPa作用下2 h的压缩量及相应的单位沉降量、孔隙比。图1-16为单位沉降量随压力变化的关系曲线。表1-37、图1-17表示压缩模量与压力的关系。
表1-36 压缩量、单位沉降量、孔隙比随压力的变化
表1-37 压缩模量随压力的变化
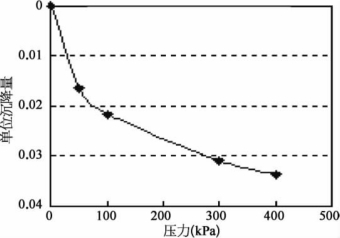
图1-16 单位沉降量随压力的变化曲线
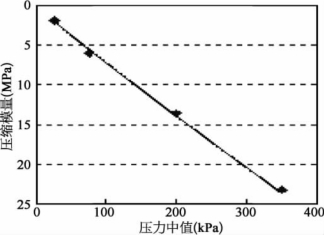
图1-17 压缩模量随压力的变化曲线
从图1-16及图1-17可以看出：
（1）压缩量Δh随着压力的增大而增大，但它们不是简单的线性关系，而是呈幂函数曲线关系。试样竖向压缩应变ε与压力P的函数关系如下：
ε＝0.004 594P 1／3R＝0.999
（2）随着压力P的增大，压缩模量E s（割线模量）愈来愈大；与黏性土相比，沙体的压缩模量较大，说明沙体的压缩性较差。压缩模量E s与压力中值P的函数关系如下：
E s＝0.095 2P 0.9412R＝0.998
式中 P——试样上作用的压力（kPa）；
E s——与压力（中值）对应的试样压缩模量（割线模量）（kPa）；
R——相关系数。
有关风积沙路基公路设计、施工与防沙的文章
- 详细阅读
-
风积沙路基公路设计-风积沙路基公路设计、施工详细阅读
应充分贯彻因地制宜、就地取材的原则。纯风积沙可采用土工布等材料来加固修筑路基，水源缺乏地区的沙基可采用振动干压实技术。沙漠路基高度应遵循满足强度、减轻沙害、保证安全、经济合理等原则，总体采取填方略大于挖方的设计原则。平沙地路段不宜取土，应加以保护。路基设计宜填挖平衡或填方略大于挖方，挖方弃土宜用于填方路基，多余弃土应置于背风一侧的低洼处，距离路堑坡顶不应小于10 m。......
2023-09-22
-
风积沙路基公路的设计、施工与防沙详细阅读
先由施工人员将土工格室张拉开，待张拉到位后，土工格室两端用钢钎固定，然后进行路基两侧包边砾石土的灌注施工，待达到设计压实度后再进行中间路槽风积沙的灌注、碾压。2）土工布的铺设对于基底处置完成和路基高度小于3 m的风积沙填筑路基段，铺设复合土工布隔断层，土工布应全路基断面铺设。......
2023-09-22
-
风积沙路基公路设计与施工防沙改进详细阅读
通过阿和沙漠公路防沙体系的效应观测，综合养护和施工的因素，对防沙体系的建立提出如下改进措施。防沙栅栏的平面布设应与路线平行，顺应地形、地势，尽量布设在迎风坡中上部。......
2023-09-22
- 详细阅读
-
风积沙路基公路设计、施工与防沙成果详细阅读
阿和沙漠公路，从K6＋000～K344＋267路段，沿线风沙地貌以高度2～10 m的中低沙丘为主，因此路线是在远离河道的前提下以长直线区段、大半径平曲线的平面线形布设的，技术指标较高。其间共有平曲线49个，交点转角7°～30°的有40个、占总数的81.63%。......
2023-09-22
-
风积沙路基公路设计、施工与防沙效果评价详细阅读
6.3.1.1 固、阻组合形式下的积沙情况阿和沙漠公路的各种固、阻防风阻沙体系，经过一年多时间使用，已出现不同程度的积沙情况，根据新疆气象服务中心于2008年3月—2009年3月的观测计算，按防风阻沙体系组合的不同及所用材料之各异，其防风阻沙性能之优劣非常明显，见表6-39、表6-40。......
2023-09-22
- 详细阅读
相关推荐