为控制围岩变形，保证支护的稳定，项目研究团队研究提出了适合大跨段的多重锁固支护施工技术。1)技术特点强挤压围岩隧道多重锁固支护施工的技术关键点为:排架式结构技术、压浆剂快速锚固锚索技术、锚索预留低预应力柔性张拉技术、三层支护技术。图6.10大跨多重锁固支护示意图图6.11排架式结构支护示意图具体实施步骤如下:①先进行多台阶分部开挖。......
2023-09-21
挤压性围岩隧道支护黏弹性分析与控制技术
【摘要】：如图5.2所示，将支护设置时刻作为坐标原点，断面被开挖出瞬间为ti=-t0，围岩与支护结构发生相互作用的时刻为ti=t1。由此即可分析围岩与支护结构在发生相互作用后的某一时刻t2的相互作用力。图5.2时间坐标根据前述的时间坐标，假定支护与围岩发生相互作用的时刻为t1，计算时刻t时支护与围岩的相互作用力为f。由Laplace变换可求得黏弹性位移的拉氏表达式，再通过Laplace逆变换即可求得黏弹性位移表达式。
如图5.2所示，将支护设置时刻作为坐标原点，断面被开挖出瞬间为ti=-t0，围岩与支护结构发生相互作用的时刻为ti=t1。由此即可分析围岩与支护结构在发生相互作用后的某一时刻t2的相互作用力。
图5.2 时间坐标
根据前述的时间坐标，假定支护与围岩发生相互作用的时刻为t1，计算时刻t时支护与围岩的相互作用力为f(t)。即当t＞t1时，围岩周边将受到释放荷载p(t)与支护作用力f(t)的共同作用并产生相应位移。
(1)隧道洞壁p(t)作用下产生的位移
假定弹性泊松比与黏弹性泊松比相等，不随时间变化，根据黏弹性第三定理可知，黏弹性体的应力与对应的弹性应力相等，黏弹性位移可由弹性-黏弹性对应原理求得。由Laplace变换可求得黏弹性位移的拉氏表达式，再通过Laplace逆变换即可求得黏弹性位移表达式。
由弹性场下的洞周位移计算式(5.2)，根据黏弹性对应定理，用s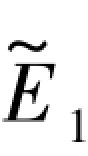 
(s)代替E，同时有
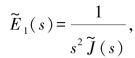则黏弹性解在象限空间的表达式为:
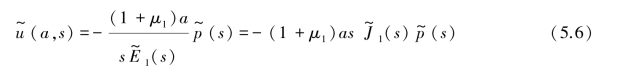
其中
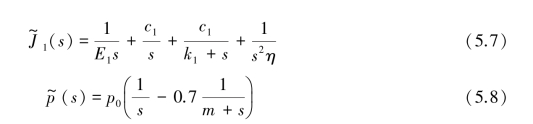
将式(5.6)、式(5.7)代入式(5.8)得:
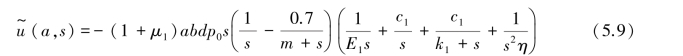
对式(5.9)进行Laplace逆变换得:
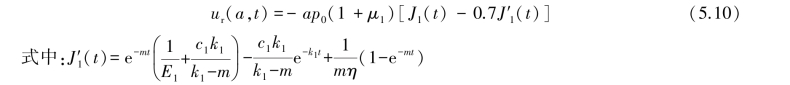
隧道开挖后，必须适时设置混凝土支护结构限制变形的进一步发展，当构筑了支护结构后，从t1～t时刻，释放荷载p(t)在洞室周边产生的位移增量为:
(2)隧道洞壁f(t)作用下产生的位移
支护结构对洞室围岩的作用力f(t)，作用方向与p(t)相反，通过弹性-黏弹性对应原理，求得从t1～t时刻f(t)在洞室周边产生的位移增量的Laplace变换表达式:
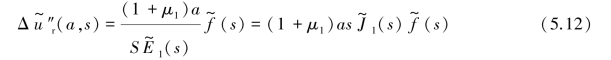
由于式中f(t)未知，根据卷积定理，可将式(5.13)的Laplace逆变换表示成积分形式，求得位移增量表达式:
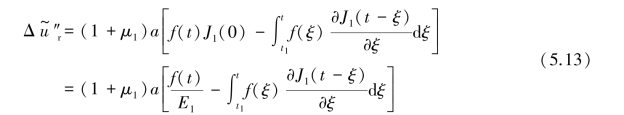
(3)隧道洞壁在p(t)和f(t)共同作用下产生的位移
施作支护后，隧道围岩在释放荷载p(t)与支护反力f(t)共同作用下，从t1～t时刻，洞室周边围岩产生的位移增量为:
(4)支护结构变形分析
根据弹性理论，支护结构在f(t)作用下的弹性径向位移为:
根据弹性-黏弹性对应法则，从t1～t时刻f(t)作用下支护结构产生的位移增量为:
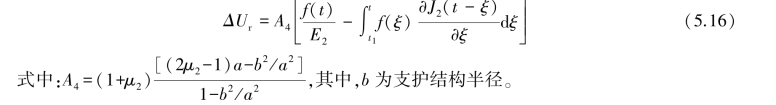
(5)围岩与支护结构变形协调分析
假设支护结构与隧道围岩的接触面上满足连续无滑移条件，则从t1～t时刻，二者径向位移增量必然相等，即:
将式(5.14)和式(5.16)代入式(5.17)得:
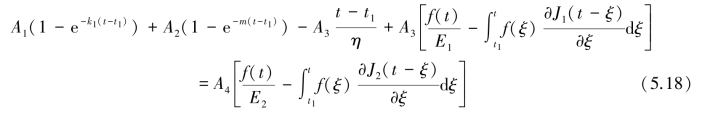
整理后得:
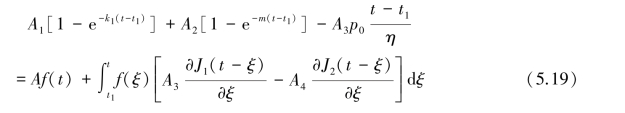
设待求函数f(t)的Laplace变换为F(s)，对式(5.20)两边进行Laplace变换，可得:
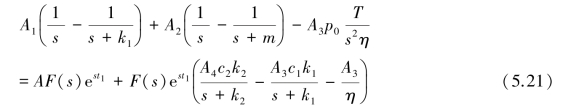
对上式进行整理可得:
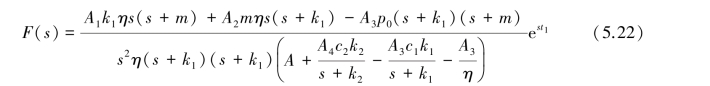
对式(5.22)两边进行Laplace逆变换，得:
参数代入式(5.22)求得F(s)表达式，并对其进行Laplace逆变换，即可求出支护结构与围岩之间相互作用随时间(蕴含空间概念)的变化规律f(t)的解析表达式，从而可求出支护结构和围岩中变形和应力随时间变化的规律。
有关挤压性围岩隧道变形破坏特性及控制技术的文章
- 详细阅读
-
挤压性围岩隧道变形破坏特性及控制技术分析详细阅读
总体变形分析按隧道的初期支护变形分级标准与可接受准则对兰渝线变形达到Ⅰ级的隧道进行分类梳理。统计分析表明，当最大主应力与隧道轴线呈大夹角时，大变形出现的频率为100%。统计分析表明，软岩大变形发生频率为64.3%，软岩夹中硬岩为30.3%，因此岩层强度是产生大变形的主要因素。兰渝线大变形隧道的统计结果表明，薄层岩体大变形出现频率为82.1%，中厚层为17.9%，厚层及以上一般不会出现大变形。表3.4各因素对围岩变形的影响程度统计分析续表......
2023-09-21
-
挤压性围岩隧道变形破坏特性与控制技术详细阅读
表1.1列出了国内外典型的挤压性围岩隧道。由此可见，高地应力软岩地质环境引起的挤压大变形破坏是一种严重的工程地质灾害。目前，对围岩挤压性大变形问题的研究，主要依靠归纳、总结及工程类比等方法，其中的主要问题集中在软岩的定义和分类、大变形的定义、机制和分级等几个方面。何满潮等将围岩大变形的判据分为定性方法和定量方法，并给出了日本学者对日本国内挤压性围岩特点及大变形判别研究方面的统计性结果。......
2023-09-21
-
挤压性围岩隧道控制技术及破坏特性详细阅读
水压致裂法地应力测量是利用一对可膨胀的橡胶封隔器，在预定的测试深度内封隔一段钻孔，然后泵入液体对该段钻孔施压，根据压裂过程曲线的压力特征值计算地应力。水压致裂法地应力测量时，破裂缝产生在钻孔岩壁上拉应力最大的部位。综上所述，水压致裂法地应力测量中，可根据试验过程中得到的相关数据来确定钻孔最大、最小水平主应力大小，同时可以根据印模器记录的裂纹破裂方向确定最大水平主应力的方向。......
2023-09-21
-
挤压性围岩隧道变形特性与控制技术详细阅读
1)技术特点新城子隧道双联拱段中隔墙厚度太薄，为确保中隔墙的稳定性，采用“背靠背”施工方法。图6.31“背靠背”施工正洞支护①先行右线施工，开挖采用三台阶机械开挖法，开挖完成后及时进行初期支护，采用电镐，将中隔墙一侧提前预埋的中下台阶接头凿出。图6.34位“背靠背”中下台阶钢拱架预埋施工照片。图6.32对拉锚杆与钢架连接示意图图6.33牛腿处的钢架连接示意图图6.34“背靠背”中下台阶钢拱架预埋施工......
2023-09-21
-
挤压性围岩隧道变形破坏特性及控制技术—非线性详细阅读
其微分型本构方程为:图4.9非线性蠕变模型一维蠕变方程当σ≤σ∞时，模型退化为Burgers模型，当σ＞σ∞时，为六元件非线性黏弹塑性模型，其一维蠕变方程为:三维蠕变方程三维应力状态下，岩石内部的应力张量可分解为球应力张量σm与偏应力张量Sij，其表达式分别如下所示:可得:σij为Kronecker函数，球应力张量σm只改变其体积，而不改变其形状;偏应力张量Sij只产生形状变化而不产生体积变化。......
2023-09-21
-
挤压性围岩隧道控制技术-改进二衬缓冲层及仰拱详细阅读
为此，项目研究团队提出二衬缓冲层及仰拱增强支护技术。2)施工工艺流程二衬缓冲层施工缓冲层结构设在拱墙初期支护与二次衬砌间，置于防水板外侧，与初支支护密贴，设缓冲结构地段，取消拱部无纺布，如图6.35所示。若施作缓冲结构导致二衬衬砌厚度小于设计厚度，则停止施作缓冲结构。图6.37仰拱施工工艺流程图图6.38仰拱支护措施示意图①仰拱开挖。......
2023-09-21
-
挤压性围岩隧道施工技术及变形控制详细阅读
1)技术特点高地应力软岩隧道大跨段至连拱过渡段施工工法关键点:大断面延伸开挖技术、双层柔性支护技术、双洞衬砌整体浇筑技术。图6.15过渡段施工工艺流程图②绑扎连拱左右线衬砌钢筋，钢筋笼定位准确，钢筋规格、间距、搭接要符合设计要求和相应规范。图6.16大跨段延伸至连拱段示意图图6.17过渡段双侧壁九部法分部示意图施工中应精确测量，严格控制堵头墙的位置，避免欠挖，减小超挖。......
2023-09-21
相关推荐