首页理论教育挤压性围岩隧道变形破坏特性控制技术-有限差分模型

挤压性围岩隧道变形破坏特性控制技术-有限差分模型

2025-09-30 理论教育版权反馈

【摘要】：参考FLAC3D手册中Burgers蠕变模型阐述，对考虑含水损伤的非线性黏弹塑性蠕变模型进行有限差分形式的转化。由于本模型可能产生塑性应变，因此Kelvin体球应变张量增量可用如下公式计算:综上，本蠕变模型的应力-应变关系可用式和式进行表征，以上差分形式可以和FLAC3D软件的指针相对应。通过相应指针读取应力张量的各个分量，根据公式—式则可求出应力强度q。

参考FLAC3D手册中Burgers蠕变模型阐述，对考虑含水损伤的非线性黏弹塑性蠕变模型进行有限差分形式的转化。数值实现中，需要将应力张量分解为球应力张量σm和偏应力张量Sij:

式中:δij——Kronecker符号。

对于Hoek体，偏应力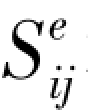 pagenumber_ebook=94,pagenumber_book=86 和偏应变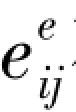存在以下关系:

式中: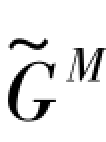 pagenumber_ebook=94,pagenumber_book=86 ——Hoek体剪切模量。对于Maxwell体，偏应力Sij与偏蠕变速率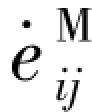关系如下:

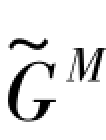式中: pagenumber_ebook=94,pagenumber_book=86 ——Hoek体剪切模量;

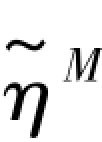pagenumber_ebook=94,pagenumber_book=86 ——黏性元件的黏滞系数。

对于Kelvin体，偏应变 pagenumber_ebook=94,pagenumber_book=86 和偏应力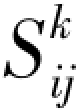的关系如下:

式中: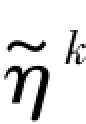 pagenumber_ebook=94,pagenumber_book=86 ——Kelvin体黏性系数;

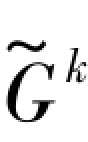pagenumber_ebook=94,pagenumber_book=86 ——Kelvin体的剪切模量。

由于编程需要，可将式(4.41)写成增量形式，可得:

式(4.44)整理后，可得Kelvin体第i步偏应变更新公式:

对于Bingham体有:

g——塑性势函数;

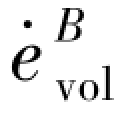pagenumber_ebook=95,pagenumber_book=87 ——Bingham体应变速率偏量;

η(n，t)=η0/tn。

由于各元件相互串联，因此应力相等，应变相加，可得:

式中:Δeij——总偏应变增量;

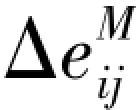pagenumber_ebook=95,pagenumber_book=87 ——Maxwell体偏应变增量;(https://www.chuimin.cn)

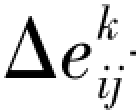pagenumber_ebook=95,pagenumber_book=87 ——Kelvin体偏应变增量;

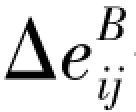pagenumber_ebook=95,pagenumber_book=87 ——Bingham体偏应变增量。

联立后可得第i步应力更新公式:

球应力张量可用差分写成增量形式:

式中: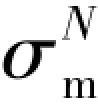 pagenumber_ebook=95,pagenumber_book=87 ——第i步球应力张量;

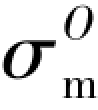pagenumber_ebook=95,pagenumber_book=87 ——第i-1步球应力张量;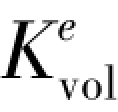——Hoek体体积模量;

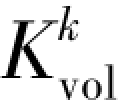pagenumber_ebook=95,pagenumber_book=87 ——Kelvin体体积模量。

由于本模型可能产生塑性应变，因此Kelvin体球应变张量增量可用如下公式计算:

综上，本蠕变模型的应力-应变关系可用式(4.13)和式(4.14)进行表征，以上差分形式可以和FLAC3D软件的指针相对应。

屈服函数实现的关键是如何让程序自动读取识别加载的应力水平，为此，本书引入应力强度概念:

由经典弹塑性力学知识可得:

式中:σm——应力球张量;

σij——应力张量;

Sij——应力偏张量。

通过相应指针读取应力张量的各个分量，根据公式(4.53)—式(4.55)则可求出应力强度q。根据应力强度的定义，单轴试验时q=σ1;等围压三轴试验时q=σ1-σ3;实现读取应力强度后，通过相关屈服函数即可实现软件自动判别屈服状态。

由于FLAC3D软件中不能使用递归函数，因此，本书蠕变参数含水率的折减修正可通过设置中间变量参与计算实现。相应的Bingham元件黏性参数的折减，本书通过对FLAC3D软件内置的ps-＞Creep指针(表征蠕变时间增量Δt)累加实现。