参考FLAC3D手册中Burgers蠕变模型阐述，对考虑含水损伤的非线性黏弹塑性蠕变模型进行有限差分形式的转化。由于本模型可能产生塑性应变，因此Kelvin体球应变张量增量可用如下公式计算:综上，本蠕变模型的应力-应变关系可用式和式进行表征，以上差分形式可以和FLAC3D软件的指针相对应。通过相应指针读取应力张量的各个分量，根据公式—式则可求出应力强度q。......
2023-09-21
挤压性围岩隧道变形破坏特性及控制技术—非线性黏弹塑性模型
【摘要】：其微分型本构方程为:图4.9非线性蠕变模型一维蠕变方程当σ≤σ∞时，模型退化为Burgers模型，当σ＞σ∞时，为六元件非线性黏弹塑性模型，其一维蠕变方程为:三维蠕变方程三维应力状态下，岩石内部的应力张量可分解为球应力张量σm与偏应力张量Sij，其表达式分别如下所示:可得:σij为Kronecker函数，球应力张量σm只改变其体积，而不改变其形状;偏应力张量Sij只产生形状变化而不产生体积变化。
1)非线性黏塑性体
试验可知，当泡水5d、15d时蠕变试验中应力水平总体上未达到炭质板岩的屈服极限强度，流变曲线没有出现第三阶段的加速蠕变段，Burgers模型能较好地描述衰减蠕变与稳定蠕变阶段。干燥状态下，应力水平130 MPa时，炭质板岩加载约5 h后，出现加速蠕变;当泡水25 d，蠕变加载至100 MPa时，出现加速蠕变，表现出明显的黏塑性变形特征。由于Burgers模型不包括塑形元件，因此无法描述炭质板岩加速蠕变阶段的黏塑性特征。
图4.6(a)是干燥状态下围压为10 MPa，荷载水平为130 MPa时轴向与侧向的加速蠕变曲线，图4.6(b)是泡水25 d，围压25 MPa，荷载水平100 MPa时轴向与侧向的加速蠕变曲线。可见，炭质板岩在加速蠕变阶段，应变随时间的增加呈非线性变化，加速蠕变规律具有幂函数的特征，函数表达式可写为:
式中:ε0——加速蠕变之前的应变值;
t——蠕变时间;
n——加速蠕变参数;
A——常数，代表应力历时状态。
对式(4.15)进行求导，有
令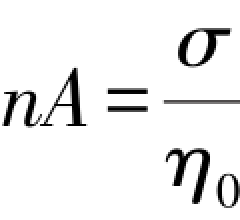
(η0为常量，是加速蠕变初期的黏性系数)，则式(4.16)可表示为:
一般黏性元件本构表达式为:
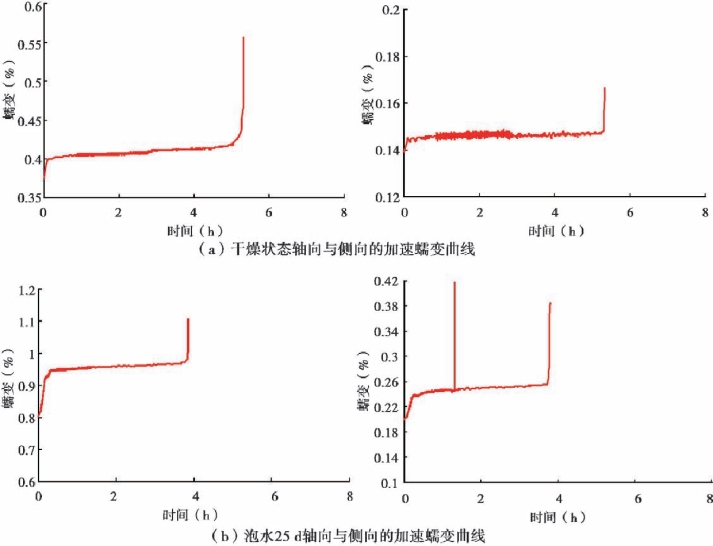
图4.6 轴向与侧向的加速蠕变曲线
比较式(4.17)和式(4.18)，可得到一个非线性黏性元件:
式中:t0——单位参考时间。
其本构方程可表示为:
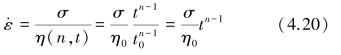
将建立的非线性黏性元件与Bingham塑性体并联起来，构成一个能描述加速蠕变的非线性黏塑性模型，如图4.7所示。
非线性黏塑性体的蠕变方程可表示为:
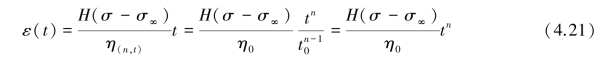
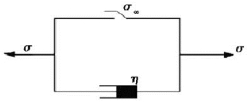
图4.7 非线性黏塑性体
式中:t0——单位参考时间，设为1;
σ∞——岩石的长期强度或者为岩石的屈服强度;
H——应力与强度相关的函数，其表达式如下:
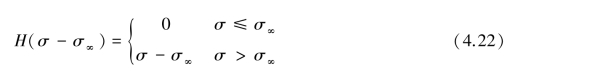
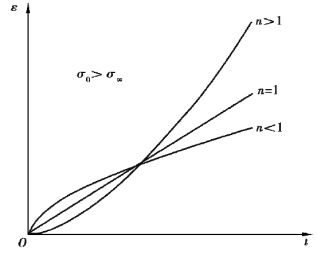
图4.8 非线性黏塑性模型的蠕变曲线
图4.8为非线性黏塑性模型在恒定应力作用下的应变与时间的关系，随时间的增加，当n＜1时蠕变速率逐渐减小，当n＞1时蠕变速率逐渐增大，当n=1时应变与时间呈线性关系。
2)非线性黏弹塑性蠕变模型
在Burgers模型串联上建立的非线性黏塑性体，就得到六元件非线性黏弹塑性蠕变模型，新模型能较好描述炭质板岩的衰减、稳定、加速蠕变阶段，如图4.9所示。
当σ≤σ∞时，非线性黏塑性体不起作用，模型退化为Burgers模型;当σ＞σ∞时，非线性黏塑性体起作用，成为六元件非线性黏弹塑性模型。其微分型本构方程为:
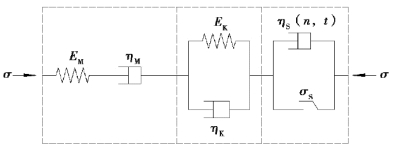
图4.9 非线性蠕变模型
(1)一维蠕变方程
当σ≤σ∞时，模型退化为Burgers模型，当σ＞σ∞时，为六元件非线性黏弹塑性模型，其一维蠕变方程为:
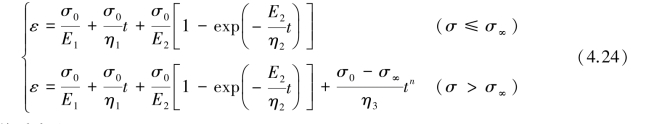
(2)三维蠕变方程
三维应力状态下，岩石内部的应力张量可分解为球应力张量σm与偏应力张量Sij，其表达式分别如下所示:
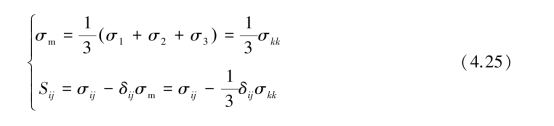
可得:
σij为Kronecker函数，球应力张量σm只改变其体积，而不改变其形状;偏应力张量Sij只产生形状变化而不产生体积变化。因此，将应变张量同样分解成偏应变张量eij和球应变张量εm:
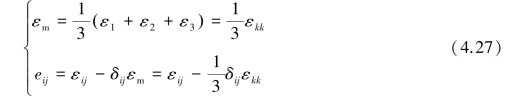
于是有:
在三维应力状态下，由虎克定律得:
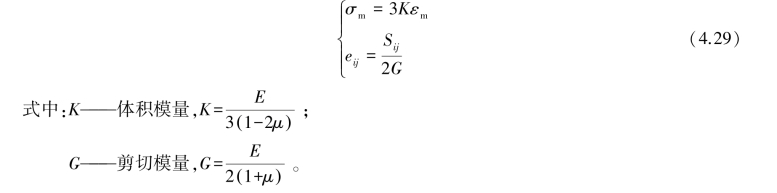
在满足材料各向同性的条件下，假设弹性应变由应力球张量引起，蠕变由应力偏张量引起，三维状态下的黏弹塑性蠕变模型的蠕变方程为:
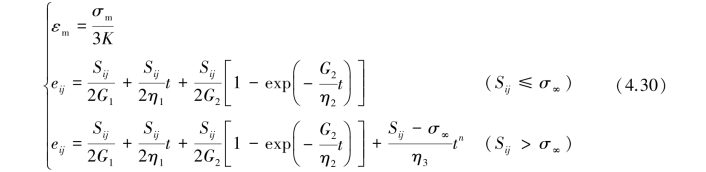
结合式(4.24)和式(4.31)，得到等围压三轴压缩应力状态下，黏弹塑性蠕变模型轴向蠕变与侧向蠕变计算公式:
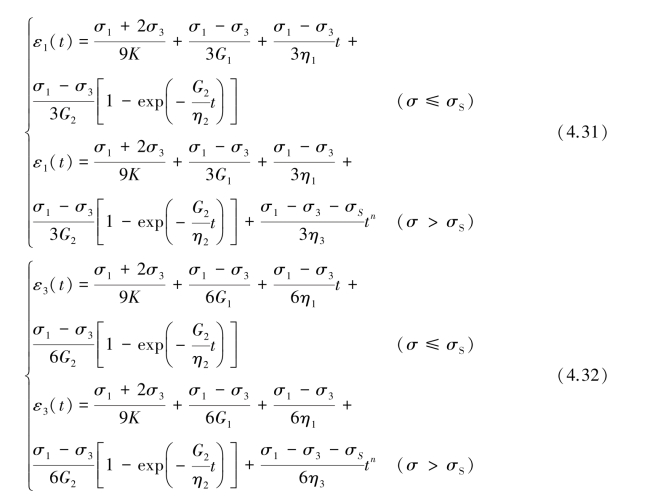
有关挤压性围岩隧道变形破坏特性及控制技术的文章
- 详细阅读
-
挤压性围岩隧道变形破坏特性及控制技术分析详细阅读
总体变形分析按隧道的初期支护变形分级标准与可接受准则对兰渝线变形达到Ⅰ级的隧道进行分类梳理。统计分析表明，当最大主应力与隧道轴线呈大夹角时，大变形出现的频率为100%。统计分析表明，软岩大变形发生频率为64.3%，软岩夹中硬岩为30.3%，因此岩层强度是产生大变形的主要因素。兰渝线大变形隧道的统计结果表明，薄层岩体大变形出现频率为82.1%，中厚层为17.9%，厚层及以上一般不会出现大变形。表3.4各因素对围岩变形的影响程度统计分析续表......
2023-09-21
-
挤压性围岩隧道变形破坏特性与控制技术详细阅读
表1.1列出了国内外典型的挤压性围岩隧道。由此可见，高地应力软岩地质环境引起的挤压大变形破坏是一种严重的工程地质灾害。目前，对围岩挤压性大变形问题的研究，主要依靠归纳、总结及工程类比等方法，其中的主要问题集中在软岩的定义和分类、大变形的定义、机制和分级等几个方面。何满潮等将围岩大变形的判据分为定性方法和定量方法，并给出了日本学者对日本国内挤压性围岩特点及大变形判别研究方面的统计性结果。......
2023-09-21
-
挤压性围岩隧道变形破坏控制技术详细阅读
为控制围岩变形，保证支护的稳定，项目研究团队研究提出了适合大跨段的多重锁固支护施工技术。1)技术特点强挤压围岩隧道多重锁固支护施工的技术关键点为:排架式结构技术、压浆剂快速锚固锚索技术、锚索预留低预应力柔性张拉技术、三层支护技术。图6.10大跨多重锁固支护示意图图6.11排架式结构支护示意图具体实施步骤如下:①先进行多台阶分部开挖。......
2023-09-21
-
挤压性围岩隧道变形破坏特性及控制技术-计算模详细阅读
计算模型在隧道围岩黏弹性分析时，为了简化运算，假设洞室截面为圆形，对于矩形或直墙拱顶的洞室采用相似变换将隧道形状作等代处理，等代圆的当量半径可按下式计算:式中:B——隧道断面最大宽度;H——隧道最大高度。取静水压力状态，洞室压力为p0，开挖半径为a，支护结构半径为b，计算模型如图5.1所示。从式(5.5)可以看出，开挖面掘进速度v越快，则p越大，释放掉的应力越小。......
2023-09-21
-
挤压性围岩隧道控制技术及破坏特性详细阅读
水压致裂法地应力测量是利用一对可膨胀的橡胶封隔器，在预定的测试深度内封隔一段钻孔，然后泵入液体对该段钻孔施压，根据压裂过程曲线的压力特征值计算地应力。水压致裂法地应力测量时，破裂缝产生在钻孔岩壁上拉应力最大的部位。综上所述，水压致裂法地应力测量中，可根据试验过程中得到的相关数据来确定钻孔最大、最小水平主应力大小，同时可以根据印模器记录的裂纹破裂方向确定最大水平主应力的方向。......
2023-09-21
-
模型验证：基于变形破坏特性及控制技术的挤压性详细阅读
图4.19三轴蠕变数值模型建立炭质板岩三轴压缩蠕变试验进行数值模拟验证，试件尺寸h=10 cm，D=5 cm。图4.20为不同含水状态下，由岩石三轴压缩蠕变模拟试验得到的试件顶点蠕变曲线与竖直方向的位移云图。如图4.20所示，三轴压缩蠕变数值试验中的自然含水状态试样在围压25 MPa下，轴向加载40 MPa、60 MPa、80 MPa、100 MPa时对应的竖向位移分别约为0.27 mm、0.36 mm、0.45 mm、0.56 mm。......
2023-09-21
-
挤压性围岩隧道的稳定性控制|变形破坏特性及控详细阅读
兰渝线围岩软弱破碎，自稳能力差，遇水易软化，受地应力和地质构造等影响，在传统锚喷复合式衬砌结构即单层支护单层衬砌施工时，往往会出现支护变形过大的现象，此时如过早施作二次衬砌则会使二次衬砌受力过大而出现开裂破损，如过晚施作二次衬砌则出现初期支护变形过大而无法保证隧道的结构稳定性。但对挤压性围岩隧道而言，隧道围岩级别越低，其选择的支护参数越高，有时需要几种支护措施联合使用。......
2023-09-21
相关推荐